6.5. Однопеременный циклический код. Код Грея

Неопределенность считывания из-за изменения кода сразу в нескольких разрядах можно ликвидировать, применив такой код, при котором переход от одного числа к соседнему сопровождался бы переменой цифры только в одном разряде.

Такие однопеременные коды можно получить, если каждому положению шкалы формально приписывать комбинацию нулей и единиц таким образом, чтобы кодовые комбинации для смежных секторов отличались только в одном разряде.

К числу однопеременных кодов относится циклический двоичный код – код Грея, получивший наибольшее распространение.

Для получения однопеременного кода можно пользоваться диаграммой Вейча, представленной на рис. 6.10.

Горизонтали и вертикали диаграммы маркируются однопеременным двухразрядным кодом.

Для получения четырехразрядного кода необходимо последовательно обойти все 16 точек пересечения горизонталей и вертикалей, дважды через точку проходить нельзя, также нельзя переходить от точки к точке по диагонали.

Рис. 6.10. Диаграмма Вейча.

Один из обходов, выделенный в диаграмме Вейча жирной линией, дает однопеременный код – код Грея.

Код для каждой точки образуется следующим образом:

- код номера горизонтали – дает два старших разряда;

- код номера вертикали – дает два младших разряда.

Например, точка «9» имеет:

- горизонталь с кодом – 11;

- вертикаль с кодом – 01;

- итого, код точки «9» - 1101.

На рис. 6.11 показана линейная шкала с кодом Грея.

Рис. 6.11. Линейная шкала с кодом Грея.

Справа от линейной кодовой шкалы приведены в виде столбцов кодов последовательность изображений десятичных чисел в коде Грея. Нетрудно видеть, что эта последовательность кодов образуется по разрядным циклам, причем значения цифр в любом цикле являются зеркальным отображением цифр соседнего цикла данного разряда.

В младшем разряде можно отметить циклы по две цифры, в следующем разряде по четыре и т.д. В столбце чисел в коде Грея (см. рис. 6.11) короткими горизонтальными черточками условно показано расположение зеркал. Эта особенность кода Грея и определила его названия, как циклического или рефлексного (отраженного).

В циклическом коде, кроме того, необходима стыковка начала шкалы с концом, в данном случае изменение одной единицы выполняется. Особенностью кода Грея является то, что вес единицы по величине в i-ом разряде определяется как

,

причем знак суммирующих членов положителен для нечетных единиц (только единиц) в числе, записанном в коде Грея, считая слева направо, и отрицателен для всех четных единиц.

В качестве примера, найдем вес числа , записанного в коде Грея.

Двоичное число приводится к циклическому кодупо формуле, где– обозначение нуля при единице разряда кода Грея,– обозначение нуля при единице разряда двоичного кода,– знак сложения по модулю 2 (mod2), т.е. без учета переноса.

Если , то.

Иными словами, для перевода двоичного числа в циклический код необходимо сдвинуть это двоичное число на один разряд вправо (при этом младший разряд теряется) и произвести поразрядное сложение поmod2 сдвинутого и несдвинутого числа А. В результате будет получено число в циклическом двоичном коде.

Пример:

Обратный переход от представления числа в циклическом коде к изображению в двоичном коде осуществляется по следующему правилу

.

Если , то

Далее

В общем виде можем записать:

Таким образом, значения разрядов двоичного числа получаются из его циклического кода Грея последовательным сложением по mod2, начиная со старшего разряда.

Пример:

Рассмотрим вариант схемной реализации устройств, преобразующих циклический код в естественный двоичный код.

На рис. 6.12 представлена структурная схема устройства для преобразования параллельного циклического кода в параллельный двоичный код. В устройстве используются двухвходовые сумматоры по mod2 – т.е. схема «исключающее ИЛИ». На рис. 6.13 представлена принципиальная схема.

Рис. 6.12. Структурная схема преобразования

циклического кода в двоичный..

Рис. 6.13. Принципиальная электрическая схема получения

параллельного двоичного кода из кода Грея.

Принципиальная электрическая схема устройства для преобразования циклического кода, поступающего последовательно, начиная со старшего разряда в последовательный двоичный код, представлена на рис. 6.14. Это устройство реализует равенство

.

Временная диаграмма представлена на рис. 6.14.

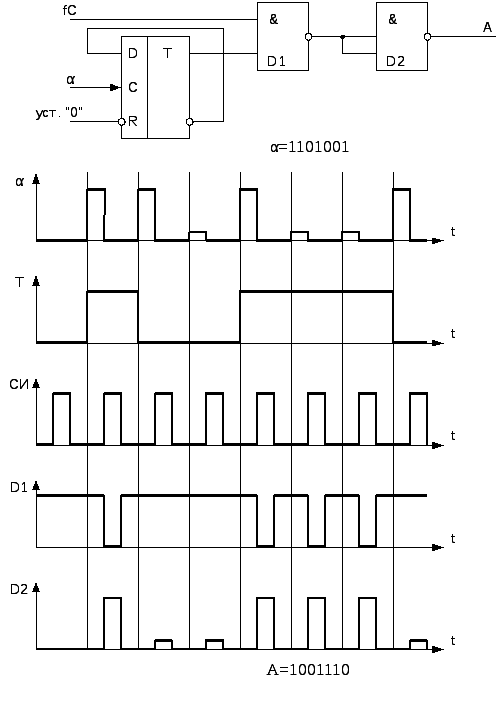
Рис. 6.14. Принципиальная электрическая схема получения

последовательного двоичного кода из кода Грея.

Триггер Т со счетным входом выполняет функции сумматора по модулю 2 последовательного действия.

Импульсы циклического кода подаются на счетный вход триггера последовательно, начиная со старшего разряда. При этом триггер перебрасывается в очередное для себя состояние с приходом каждого импульса, соответствующего 1 в циклическом коде.

Единичный выход триггера связан с одним из входов вентиля D1, на второй вход которого поступают синхроимпульсы .

Импульсы сдвинуты относительно импульсов циклического кода на полпериода.

На временной диаграмме показано преобразование кода в двоичный кодА.

В вычислительных устройствах последовательного действия арифметические операции над последовательными кодами чисел производятся с младших разрядов. Для таких устройств существует метод, позволяющий выполнить перевод циклического кода в обычный двоичный код, начиная с младшего разряда. Данный метод подробно расписан в специальной литературе.

Считывание информации в коде Грея можно получить с обычной двоичной кодовой шкалы, расположив соответствующим образом считывающие элементы на каждой разрядной дорожке относительно линии считывания. На рис. 6.15 показан пример считывания пятиразрядного кода Грея с четырехразрядной двоичной кодовой шкалы.

Рис. 6.15 5-тиразрядный кода Грея с 4-хразрядной двоичной кодовой шкалы.

Считывающие элементы 2-5 разрядов сдвинуты относительно опорной линии СС' на ½ кванта соответствующего разряда, в направлении увеличения чисел. Для считывания одного разряда считывающий элемент располагают на грубой разрядной дорожке, на опорной линии СС'.

Вообще говоря, в чисто двоичной кодовой шкале благодаря периодичности картины прозрачных и непрозрачных кодовых участков имеется возможных положений для считывающего элемента наК-ой разрядной дорожке. Считывающий элемент может быть установлен в любом из этих положений, если это необходимо из конструктивных соображений.

Из рисунка кода Грея видно, что длина светлых участков всех разрядов, кроме старшего, шкалы кода Грея в 2 раза больше, чем при двоичном кодировании. Это позволяет вдвое повысить разрешающую способность преобразователя, применяя код Грея, вместо обычного двоичного кода.

Однако следует отметить, что допуски на изготовление кодовой шкалы Грея и регулировку считывающих элементов значительно более жесткие, чем для кодирующих устройств с логическим считыванием с двоичной маски.