2. Квантование непрерывных величин во времени и по уровню

Процесс преобразования непрерывной величины в дискретную заключается в представлении непрерывной величины последовательным во времени рядом её мгновенных квантованных по уровню значений.

При этом преобразовании обычно имеет место два вида квантования:

- квантование по времени;

- квантование по уровню.

Процесс квантования вносит в преобразуемую информацию ряд специфических погрешностей.

2.1. Квантование во времени

Квантование во времени непрерывных сообщений есть процесс преобразования функции непрерывного времени в функцию дискретного времени, представляемую совокупностью координат (величин), по значениям которых может быть получена оценка исходного непрерывного сообщения.

В самом общем виде дискретное представление непрерывного сообщения на интервале Т совокупностью координат сообщения и последующее восстановление по ним исходного сообщенияможно записать в виде:

,

где – оператор представления (приближающая функция),– оператор восстановления (воспроизводящая функция).

–текущая погрешность дискретного представления.

Операторы ив общем случае могут быть как нелинейными, так и линейными, причём с одним и тем же оператором представлениямогут быть использованы разнообразные операторы восстановления, и наоборот. При этом функциииявляются базисными функциями.

Оператор может быть в виде:

- коэффициентов некоторого ряда (ряды Фурье и Котельникова, степенные полиномы и т.д.);

- выборками;

- конечными разностями.

В частном случае, когда координаты x_i представляются в виде , гдеk – номер интервала, т.е. они являются выборками (непосредственными отсчётами) исходного сообщения, то оператор осуществляет аппроксимацию.

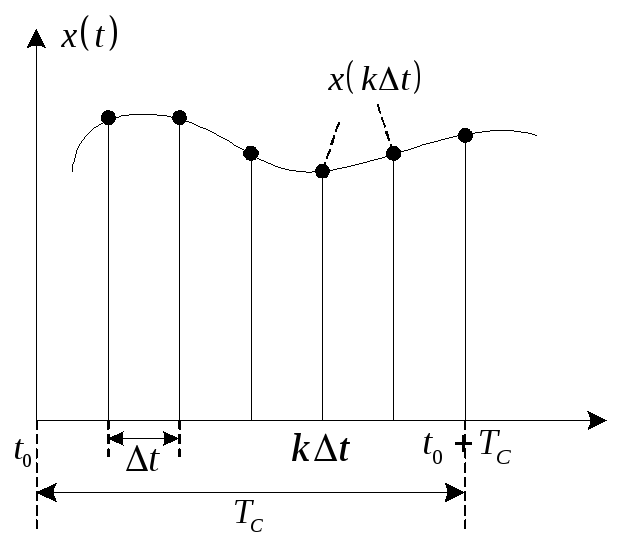
При процесс квантования во времени соответствует фиксации мгновенного значения аналоговой величины в дискретные моменты времени.

При такой замене из рассмотрения исключается всё множество значений функции, находящейся внутри интервала .

Полученную функцию часто называют решетчатой.

Дискретизация по времени может быть равномерной (принудительной), когда интервал дискретизации остаётся неизменным, и неравномерным, когдаи меняется в соответствии с каким-либо параметром сообщения, например, в соответствии со скоростью изменения сообщения во времени, так называемая адаптивная дискретизация. Адаптивная дискретизация бывает с кратными и некратными интервалами.

Теоретическое рассмотрение и практическая реализация адаптивной дискретизации представляет трудности. В настоящее время наиболее широкое применения нашла равномерная дискретизация.

В основе математического описания дискретизации непрерывных сообщений по времени лежит так называемая импульсная функция дискретизации – , которая представляет собой периодическую последовательность– функций, следующих через интервалы времени

.

Дискретизация непрерывной функции времени с математической точки зрения представляет собой умножение этой функции на импульсную функцию дискретизации:

.

В соответствии с фильтрующими свойствами – функции можно записать:

.

Следовательно, умножение сообщения на импульсную функцию дискретизации приводит к образованию периодической последовательности- импульсов, веса которых равны мгновенным значениям сообщения в моменты времени, то есть в моменты взятия отсчётов. По сути дела такое преобразование эквивалентно получению амплитудно-модулированной последовательности импульсов (АИМ), в данном случае с глубиной модуляции(униполярная последовательность).

При решении задачи дискретизации непрерывных сообщений возникает ряд вопросов:

- из каких соображений необходимо исходить при выборе интервала дискретизации ;

- какова точность замены непрерывного сообщения последовательностью его отсчётов, взятых в дискретные моменты времени;

- каков максимально допустимый интервал дискретизации , при котором еще принципиально возможно восстановление непрерывного сообщения по его отсчётам.

Получить ответ на эти и другие вопросы можно, если проблему дискретизации по времени рассматривать в неразрывной связи с обратной проблемой – восстановлением непрерывной функции времени по её мгновенным значениям.

Очевидно, что чем меньшим количеством отсчётов заменяется сообщение длительностью , то есть продолжительнее интервал дискретизациии тем сложнее выполнить восстановление исходной функции, и наоборот.

Таким образом, при реализации квантования по времени возникает задача выбора частоты квантования и метода аппроксимации с тем чтобы иметь возможность восстановить затем исходную непрерывную функциюс заданной точностью(– оценка исходной функции).

Тогда, задача дискретизации может быть сформулирована следующим образом: для данной непрерывной функции , определенной на отрезке [a,b], найти функции и, гдеS – выбранный класс функций, для которых число разбиений на отрезка [a,b] минимально и .– интервал дискретизации во времени,– заданная предельная погрешность.

Существует широкий класс сигналов подлежащих преобразованию из непрерывной формы в дискретную. Например: сигналы об изменение дальности до подвижного объекта, его угловые координаты, скорость изменения угловых координат и т.д. – сигналы монотонные во времени, детерминированные; речевой сигнал – сигнал, обладающий квазистационарными свойствами. Таким образом к вопросу квантования и восстановления функции нельзя подойти однозначно.

Существует несколько подходов к решению указанной задачи.

1. На основе частотного критерия, который учитывает спектральный состав функции (теорема Котельникова) – для сигналов, обладающих квазистационарными свойствами.

2. Рассматривать задачу квантования как задачу аппроксимации, при этом построение аппроксимирующей, то есть приближающей функции, можно проводить различными путями: интерполированием, среднестепенным приближением, равномерным приближением и т.д.

Для систем управления нашли применение интерполирование 0, 1 и 2 порядка, то есть ступенчатая, линейная и параболическая аппроксимирующая функция.