5.7.5 Генератор управляемый напряжением (гун)

Для построения схемы ГУН могут быть использованы разные способы.

ГУН, построенный по схеме интегратора со сбросом, представлен на рис. 5.25.

На усилителе У1 собран интегратор, в обратную связь которого включен ключ, разряжающий емкость при своем включении.

Выход интегратора соединен со входом порогового устройства.

,

,

.

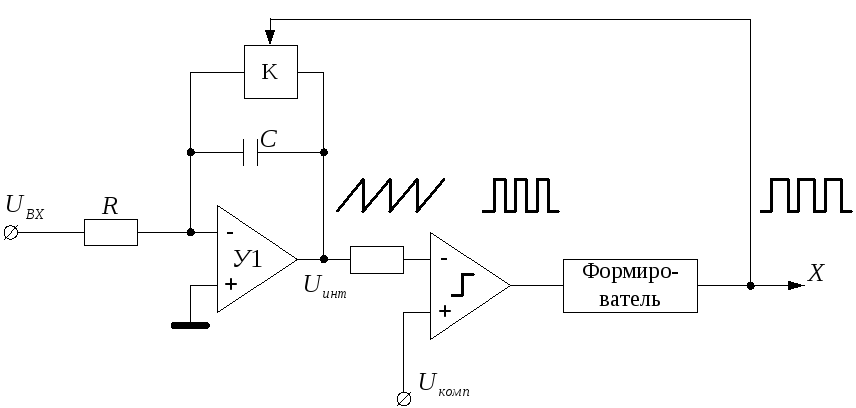
Рис. 5.25. Схема однополярного ГУН.

Как только достигнет напряжения, поданного на второй вход порогового элемента, компаратор сработает и запустит формирователь импульсов, который, в свою очередь, откроет ключ в обратной цепи интегратора и разрядит емкость, тем самым, после чего начинается новый процесс интегрирования.

Периодический сброс интегратора в данной схеме устраняет проблему дрейфа нуля. Стабильность частоты составляет примерно 0,1%.

Двухполярный ГУН (см. рис. 5.26).

Рис. 5.26. Схема двухполярного ГУН.

Существуют и другие способы построения ГУН – на управляемых мультивибраторах.

Управляемый мультивибратор (см. рис. 5.27).

Принцип работы ГУН основан на управлении током перезарядки конденсатора мультивибратора посредством управляемых генераторов тока на транзисторах.

Рис. 5.27. Структурная схема ГУН К531ГГ1.

Вход Упр1 регулирует диапазон частот вырабатываемых ГУН, а вход Упр2 управляет непосредственно выходной частотой ГУН (К531ГГ1). Диапазон выходной частоты составляет от 1 Гц до 60 МГц.

5.8. Архитектура сигма-дельта ацп

Своим названием такой АЦП обязан двум блокам: – наличию интегратора,– наличию дифференциального усилителя.

Одним из принципов, заложенных в такого рода АЦП, позволяющих уменьшить погрешность вносимую шумами, а следовательно, увеличить разрешающую способность – это усреднение результатов измерения.

В сигма-дельта АЦП аналоговый сигнал квантуется с очень низким разрешением (как правило 1 бит), на частоте, во много раз превышающей максимальную частоту спектра сигнала.

Используя эту методику передискретизации в сочетании с цифровой фильтрацией, можно значительно повысить разрядность.

Для снижения эффективной скорости поступления отсчётов на выходе АЦП применяется децимация.

Передискретизация.

При классическом подходе к процессу дискретизации:

–частота среза.

Значительная часть шума квантования попадает в рабочую полосу частот. При соблюдении теоремы Котельникова полоса частот полезного сигнала меньше, либо равна . Таким образом, аналоговый фильтр на входе преобразователя должен обладать высокой крутизной спада АЧХ за полосой пропускания, для эффективного ослабления шумов и помех, проникающих в рабочую полосу в результате интерференции с гармониками частоты дискретизации. Обычно это активные фильтры, у которых добиться высокого подавления гармоник и малых фазовых искажений задача противоречивая.

Другой способ – передискретизация.

При этом входной сигнал квантуется с частотой (- отношение передискретизации), а частота выходного цифрового потока равна.

В этой схеме два новых элемента – цифровой фильтр и дециматор.

Шум квантования в полосе частот от доподавляется цифровым фильтром в выходном потоке. Это приводит к улучшению отношения сигнал-шум и можно добиться малой неравномерности АЧХ и ФЧХ цифрового фильтра и высокой линейности. Сам же аналоговый фильтр вырождается в простоеRC звено. К сожалению, цена за сверхразрешение высока, потому что для улучшения отношения сигнал-шум на 6 дБ (1 бит в два раза) требуется увеличить коэффициент передискретизации в 4 раза.

Для сохранения значения этого коэффициента в разумных пределах можно разбить спектр шума квантования так, чтобы основная его часть была между и, и только малая часть оставалась в области. Эту функцию выполняет сигма-дельта модулятор. После такого распределения цифровой фильтр легко подавит значительную часть энергии шума квантования, а общее отношение сигнал-ум, определяющее динамический диапазон, ощутимо возрастёт.

Схема сигма-дельта АЦП первого порядка представлена на рис. 5.25.

Линейная модель модулятора представлена на рис. 5.26.

1. Передаточная функция по входу :

,

где – интегратор,– квантователь.

Рис. 5.25. Схема сигма-дельта АЦП первого порядка.

Рис. 5.26. Линейная модель модулятора.

2. Передаточная функция по входу :

.

Выходной сигнал равен

.

Отсюда следует, что для низкочастотного сигнала имеется НЧ фильтр первого порядка, а для шума квантования наоборот фильтр ВЧ, то есть подъём сигнала с возрастанием частоты.

Такой модулятор называют шумообразующим.

Цифровая фильтрация

Цифровой фильтр должен ослаблять переотражения от выходной частоты преобразования , подавлять продукты, в том числе и компонент, шумообразующего процессамодулятора, а так же проводить децимацию (см. рис. 5.27).

Рис. 5.27. Цифровая фильтрация.

1. Фильтр конечных последовательностей (FIR) – обычно на каждый входной отсчёт приходится один выходной, если надо децимировать на более низкую частоту, можно выдавать более редко данные, то есть на каждый отсчёт пересчитывается конечная последовательность в соответствии с весами (весовая функция) более стабильны и предпочтительны (увеличиваются аппаратные затраты).

2. Фильтр бесконечной последовательности, каждый входной сигнал соответствует выходному – децимация делается самостоятельно.