5.2.3. Особенности применения метода моментов

1. Моментные оценки параметров т_х, D_x, σ_х, C_s, как это следует из формул (5.7) — (5.10), не зависят от закона рас­пределения (в других методах оценки параметров могут зависеть от закона распределения). Это свойство моментных оценок в зна­чительной степени упрощает их практическое использование и, во многом, именно поэтому эти оценки первыми вошли в практику статистических расчетов и получили такое большое распространение.

2. Эмпирическое математическое ожидание или среднее значе­ние является несмещенной и состоятельной оценкой математического ожидания.

3. Рассмотренные оценки дисперсии, коэффициента вариации и асимметрии смещены. Поправочные множители, которые вводятся в выражения (5.7) — (5.10), ликвидируют погрешность в значениях выборочных моментов μ₂ и μ₃, однако при этом соответствующее исправление оценок C_v и C_s достигается не всегда.

Как показано Е. Г. Блохиновым [9], смещенность (отрицатель­ная) оценки коэффициента вариации C_v, определенная по формуле (5.9), невелика и становится практически ощутимой лишь при большой асимметрии.

Смещенность (отрицательная) оценки коэффициента асимметрии С_s по формуле (5.10) и соответственно отношения C_s/C_v гораздо больше и составляет десятки процентов. При большой асимметрии (C_s >3 — 4C_V) и больших C_v смещенность так велика (при этом уже какие-либо поправки не могут быть введены принципиально), что метод моментов теряет право на применение.

4. Эффективность моментных оценок часто невысока.

Все это позволяет сделать вывод, что применение метода мо­ментов в геоэкологических расчетах должно быть ограничено и в некоторых случаях он должен быть заменен методами, дающими оценки бо­лее высокой эффективности.

5.2.4. Оценка случайных погрешностей выборочных числовых характеристик методом моментов

Погрешность средних значений в общем виде определяется по формуле

(5.11)

При нормальном законе распределения распределение также подчиняется нормальному закону распределения. При асимметричном законе распределения распределение имеет асимметричный характер. В этом случае для оценки погрешностей той или иной обеспеченности может быть использован закон распределения Стьюдента (см. гл. 6).

В общем случае средняя квадратическая погрешность оценки дисперсии может быть аналогично выражению (5.11) представлена в виде

(5.12)

где – среднее квадратическое отклонение

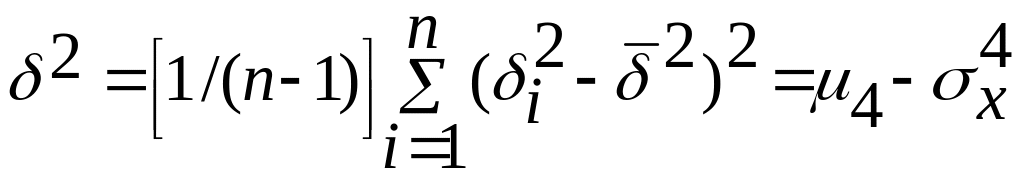(5.13)

δ – центрированное значение случайной величины (см.формулу 3.25)

Для распределения Пирсона Ш типа в соответствии с формулами (5.12) и (5.13) получаем

(5.14)

откуда при С_S=0, т. е. для нормального распределения,

, (5.13)

а при Cs = 2C_v, т. е. для гамма-распределения,

. (5.14)

Средняя квадратическая погрешность среднего квадратического отклонения вычисляется по формуле

(5.15)

Средняя квадратическая погрешность определения коэффици­ента вариации в общем случае для распределения Пирсона III типа рассчитывается по формуле [1, 30]

(5.16)

Отсюда при отсутствии внутрирядной связи и нормальном за­коне распределения

(5.17)

и при гамма-распределении, то есть C_s = 2 С_v ,

(5.18)

Для распределения Крицкого-Менкеля теоретические выводы стандартных погрешностей расчета коэффициента вариации отсутствуют. Сопоставление погрешностей C_v распределения Крицкого-Менкеля и Пирсона III типа, показало, что для их оценки могут использоваться ранее представленные формулы.