II. Преобразования координат при переходе к новому базису.
Пусть в n-мерном линейном (векторном) пространстве Rn заданы два базиса:
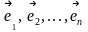(старый)
(новый)
Векторы нового базиса выражаются через векторы старого базиса следующим образом:
+
+…+
=
+
+
…+
…………………………………..
=
+
+…+
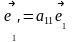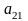
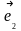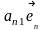
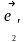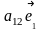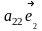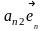
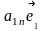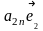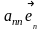
def.
Матрица А=
называется матрицей
перехода от
старого базиса
,
,…,
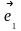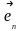к
новому
(или матрицей линейного преобразования).
Матрица А – невырожденная, значит для матрицы А существует обратная А-1.
Рассмотрим
как связаны координаты одного и того
же вектора
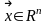в
старом и новом базисах.
Пусть
x1,…,xn
– координаты
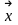в
старом базисе
,…,
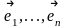
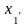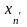– координаты
в
новом базисе
.
=
.
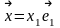
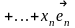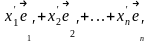Можно доказать:
,
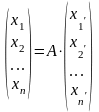где А
– матрица перехода от
,…,
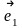к
.
или
=
А-1
Эти формулы называются формулами преобразования координат.
Пример
9.2. Пусть
вектор
имеет
координаты (1, 2)
в базисе
.
Найти
координаты этого вектора в базисе
,
.
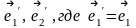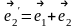§10. Собственные векторы и собственные значения
def.
Ненулевой
вектор
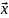
называется собственным
вектором
линейного
преобразования А
(матрицы А),
если найдется такое число
,
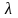что выполняется равенство
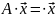(1)
Число называется собственным значением линейного преобразования А, соответствующим собственному вектору .
Если
линейное преобразование А
в базисе
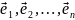имеет матрицу
А=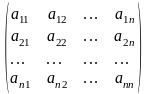
,
то
равенство (1) можно записать в матричной
форме
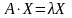или
,
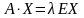где Е
– единичная матрица. Следовательно,
,
где
,
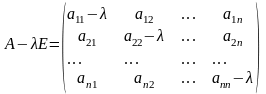Х
=
.
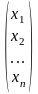Перейдем к координатной форме записи
.
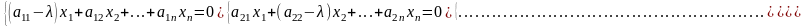(2)
Для того чтобы эта однородная система n уравнений с n неизвестными имела ненулевые решения необходимо и достаточно, чтобы ее определитель был равен нулю.
=
0 (3)
Уравнение (3) называется характеристическим уравнением матрицы А.
Корни характеристического уравнения являются собственными значениями матрицы А (характеристические числа).
Каждому собственному значению соответствует собственный вектор, координаты которого находят из системы (2) при соответствующем значении .
Пример 10.1. Найти собственные значения и собственные векторы матрицы
А
=
.
Пример 10.2. Найти собственные значения и собственные векторы матрицы
А
=
.
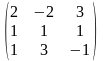