- •Лекция №5 (продолжение)
- •§7. Скалярное произведение векторов
- •I. Определение
- •II. Свойства скалярного произведения
- •Условие перпендикулярности векторов
- •III. Скалярное произведение векторов, заданных координатами
- •IV. Угол между векторами в пространстве
- •V. Приложение скалярного произведения к механике
- •§8. Векторное произведение векторов
- •Определение
- •II. Свойства векторного произведения
- •III. Векторное произведение векторов, заданных координатами
- •§9. Линейные отображения. Преобразования координат.
- •I. Основные понятия
- •II. Преобразования координат при переходе к новому базису.
- •§10. Собственные векторы и собственные значения
Лекция №5 (продолжение)
§7. Скалярное произведение векторов
I. Определение
def.
Скалярным
произведением
векторов
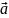 и
и
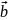 называется число, равное произведению
модулей этих векторов на косинус угла
между ними.
называется число, равное произведению
модулей этих векторов на косинус угла
между ними.
 .
(1)
.
(1)
Придадим (1) другой вид (по свойству 1 проекций).
 проекция
на ось, определяемую
.
проекция
на ось, определяемую
.
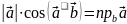 проекция
на ось, определяемую
.
проекция
на ось, определяемую
.
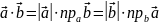 .
(2)
.
(2)
II. Свойства скалярного произведения
Коммутативность умножения:
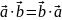 .
.
Доказательство. Справедливость утверждения непосредственно следует из определения скалярного произведения.
Ассоциативность относительно скалярного множителя:
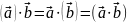 .
.
Доказательство.
Пусть
 Тогда
Тогда
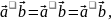

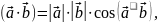
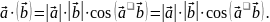
2)
 Доказать
самостоятельно.
Доказать
самостоятельно.
Дистрибутивность умножения относительно сложения:
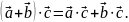
Доказательство.
Пример 7.1.
Векторы
и
образуют угол
 Зная, что
Зная, что
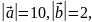 вычислить
вычислить
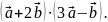
Условие перпендикулярности векторов
По
определению

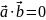 ,
если
,
если
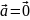 или
или
 ,
или
,
или
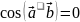 ,
т.е.
,
т.е.
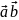 .
Пусть
.
Пусть
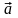 и
и
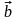 – ненулевые векторы. Тогда
– ненулевые векторы. Тогда
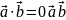 .
.
Итак, для того, чтобы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.
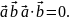
Пример
7.2. При каком
значении векторы
векторы
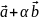 и
и
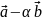 ортогональны,
если
ортогональны,
если
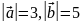 ?
Ответ:
?
Ответ:
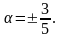
III. Скалярное произведение векторов, заданных координатами
Даны
два вектора
= ax
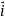 + ay
+ ay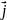 + az
+ az
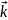 и
= bx
+ by
+ bz
.
Найти
и
= bx
+ by
+ bz
.
Найти
 .
.
Найдем предварительно скалярное произведение ортов.
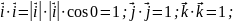

Тогда
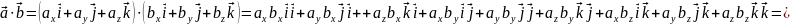
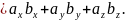
 скалярное
произведение векторов, заданных
координатами.
скалярное
произведение векторов, заданных
координатами.
Если
,
то
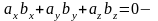 условие
перпендикулярности векторов, заданных
координатами.
условие
перпендикулярности векторов, заданных
координатами.
Пример
7.3. При каком
значении c
векторы
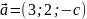 и
и
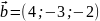 взаимно перпендикулярны.
взаимно перпендикулярны.
IV. Угол между векторами в пространстве
По
определению
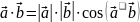 ,
значит
,
значит
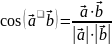 .
.
Если векторы заданы координатами, т. е. = ax + ay + az и = bx + by + bz , то

 .
.
Пример 7.4. Даны вершины четырехугольника А (1, 2, 2), В (1, 4, 0), С (4, 1, 1),
D
(5,
5,
3). Вычислить угол
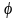 между
его диагоналями. Ответ:
между
его диагоналями. Ответ:
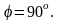
V. Приложение скалярного произведения к механике
Если материальна
точка, на которую действует сила
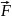 совершает перемещение по вектору
совершает перемещение по вектору
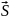 ,
то работа А
равна скалярному произведению
и
.
,
то работа А
равна скалярному произведению
и
.
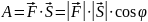 .
.
Пример
7.5. Вычислить
работу равнодействующей
сил
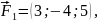
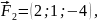
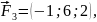 приложенных к
материальной точке, которая под их
воздействием перемещается прямолинейно
из т. М1
(4, 2, 3)
в т. М2
(7, 4, 1).
приложенных к
материальной точке, которая под их
воздействием перемещается прямолинейно
из т. М1
(4, 2, 3)
в т. М2
(7, 4, 1).
Решение.
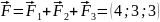 ,
,
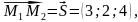
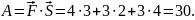
§8. Векторное произведение векторов
Определение
def.
Векторным произведением
вектора
на вектор
называется вектор
 ,
который определяется следующим образом:
,
который определяется следующим образом:
модуль вектора численно равен площади параллелограмма, построенного на векторах и как на сторонах
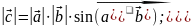
2) вектор
перпендикулярен перемножаемым векторам,
т. е.
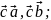
3) направление вектора таково, что если смотреть с его конца (вдоль вектора), то поворот по кратчайшему пути от вектора к вектору виден совершающимся против часовой стрелки.
(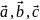 ориентированы как
ориентированы как
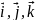
прав. тройка).
прав. тройка).
Обозначается:
 или
или
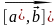 .
.
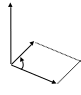
Частные случаи: