Лекція 11. Хвильові алгоритми обходу сайтів

Обхід сайтів, властивості алгоритмів обходу, організація обходу сайтів. Алгоритми обходу сайтів: повного графа, тора, гіперкуба, Таррі. [1, Лекція 14]

Алгоритмом обходу називається алгоритм, що володіє наступними трьома властивостями.

1) У кожному обчисленні один сайт-ініціатор, який починає виконання алгоритму, посилає рівно одне повідомлення.

2) Процес сайту, отримуючи повідомлення, або посилає одне повідомлення далі, або виконує процедуру return(ОК).

3) Алгоритм завершується в ініціаторі і до того часу, коли це відбудеться, процес кожного сайту посилає повідомлення хоча б один раз.

З перших двох властивостей випливає, що в кожному скінченному обчисленні рішення при-ймає рівно один процес. Кажуть, що алгоритм завершується в цьому процесі.

У кожній досяжної конфігурації алгоритму обходу або передається рівно одне повідомлення, або рівно один процес отримав повідомлення і ще не надіслав відповідне повідомлення.

З більш абстрактної точки зору, повідомлення в обчисленні, взяті разом, можна розглядати як єдиний об'єкт (маркер), який передається від процесу до процесу, і, таким чином, «відвідує» всі процеси. У наступній лекції алгоритми обходу використовуються для побудови алгоритмів вибору і для цього важливо знати не лише загальну кількість переходів маркера в одній хвилі, але і скільки переходів необхідно для того, щоб відвідати перші k процесів.

Алгоритм обходу повного графа

Повний граф містить всі можливі зв'язки між вершинами. Нехай n – кількість вузлів у повному графі. По відношенню до даного вузла this-ініціатору позначимо множину інших вершин повного графа: {u₁, u₂, .., u_{n – 1}}.

Повний граф можна обійти шляхом послідовного опитування. Цей алгоритм подібний до відповідного алгоритму з попередньої лекції, але за один раз опитується тільки один сусід ініціатора. Тільки коли отримано відповідь від одного сусіда, опитується наступний. Таким чином, повідомлення з номером (2i – 1) – це опитування для сайту u_i, а повідомлення з номером 2i – відповідь цього сайту. Всього ж за час виконання відбувається обмін 2(i – 1) повідомленнями.

Алгоритм послідовного опитування:

var i: integer init 0; (* лічильник *)

Для ініціатора:

begin

while i < n – 1 do

begin out token to u_i+1 ;

receive token; i := i + 1

end;

return(OK)

end

Процес сайту не-ініціатора:

begin

receive token from u;

out token to u

end

Алгоритм обходу тора

Граф виду «тор» являє собою сітку з додатковими ребрами, що з'єднують вершини з верхнього ряду («рядки») решітки з вершинами з нижнього ряду, а також з ребрами, що з'єднують вершини з лівого ряду («стовпця») решітки з вершинами з правого ряду. Таким чином, виникають додаткові цикли. Кожна вершина тора (на відміну від решітки) має ступінь 4, тобто граф є регулярним. При стандартному зображенні такого графа кожна вершина має «лівого» сусіда, «правого» сусіда, «верхнього» сусіда, «нижнього» сусіда (рис. 11.1). Тор, побудований на основі решітки m  n, містить mn вузлів і 2mn ребер. Кількість ребер можна підрахувати як безпосередньо, так і на основі відомої теореми теорії графів: «сума ступенів вузлів дорівнює подвоєному числу ребер».

Рисунок 11.1 – Тор 3  5. Ребра різних напрямків.

З-за його регулярних властивостей тор або його модифікації часто використовуються в різ-них архітектурах. Наприклад, одна з перших архітектур багатопроцесорних ЕОМ ILLIAC-IV використовувала тороподібне з'єднання процесорів.

Ідея алгоритму полягає у тому, що потрібно обійти всі вузли тора m  n (але не всі ребра). Ініціатором-початковим вузлом при обході може бути будь-який з вузлів. Алгоритм орієнтований на топологію тора, але на сайтах немає глобальної інформації про топологію, є лише імена ребер (L, R, U, D – рис. 11.1), які визначають напрями у відповідності з наведеним вище рисунком. Їх можна вважати локальним знанням про топологію.

Дії ініціатора (виконується один раз):

out (token, 1) through U

Дії процесу кожного сайту при отриманні маркера (token, k):

begin

if k = m*n then return(OK)

else if (kmodn = 0) then out (token, k+1) through U

else out (token, k+1) through R

end

На рис. 11.2 показаний порядок обходу тора 3  4. Зірочкою позначено сайт-ініціатор обходу, а літерами «оk» – сайт, який повідомляє про завершення обходу. Близько ребра записано число – значення k, яке передається по цьому ребру від одного сайту до іншого.

Рисунок 11.2 – Порядок обходу тора 3  4

Алгоритм обходу гіперкуба

В теорії графів відомий клас графів Q_n, званих кубами розмірності n, або гиперкубами. Це сімейство описується формулами Q_n = K₂  Q_{n – 1} , Q₁ = K₂. Тут K₂ – повний граф з двома вершинами, тобто це дві вершини, з'єднані одним ребром. Операція «» – перемножування графів.

Ця операція для графів A і B визначається наступним чином.

Результатом операції є граф C = A  B, множина вершин якого полягає у взаємнооднозначному відношенні з декартовим добутком множин вершин графів A і B, V(C) = V(A)  V(B).

Множина ребер E(C) графа C породжується множинами ребер E(A) і E(B). Нехай вершина v₁V(C) відповідає парі вершин (a₁ , b₁), a₁  V(A), b₁  V(B), а вершина v₂  V(C) відповідає парі вершин (a₂ , b₂), a₂  V(A), b₂  V(B), тоді v₁ смежна з v₂ (між ними є ребро), якщо виконується одна з двох умов:

1) a₁ = a₂ і b₁ смежна b₂;

2) b₁ = b₂ і a₁ смежна a₂.

Гіперкуб Q₁ = K₂, тобто являє собою «відрізок» з точки зору зображення геометричних фігур. Він містить 2 вершини. Степінь кожної з них дорівнює одиниці. Гіперкуб Q₂ з точки зору теорії графів являє собою цикл із чотирьох вершин, в геометричному поданні – квадрат. Степінь кожної вершини дорівнює 2. Гіперкуб Q₃ може бути представлений вершинами і ребрами геометричної фігури у тривимірному простірі – куба. Цей гіперкуб містить 8 вершин степеня 3.

У загальному випадку гіперкуб Q_n містить 2n вершин степеня n. У зв'язку з цим зручно кодувати вершини рядками з n біт – двійковій формою номерів вершин: від 000...0 до 111...1. Лівий розряд числа (символ рядка) будемо називати нульовим розрядом, правий – (n – 1)-м. Тоді дві вершини в гіперкубі є суміжними, якщо їх коди відрізняються в точності одним бітом. Наприклад, суміжними з вершиною з кодом 010 будуть вершини з кодами 110, 000, 011.

У кожному вузлі u інцидентні йому ребра можна перенумерувати числами від 0 до n – 1 так, що ребро з номером 0 буде єднати вузол u з таким вузлом гіперкуба, код якого відрізняється від коду u в нульовому розряді. Відповідно, ребро з номером 1 йде до вершини з кодом, який відрізняється від коду u в першому розряді і т. д. Це так званий код Грея.

На рис. 11.3 представлений тривимірний гіперкуб (лівий), у якого біля вершин розташовані відповідні коди, причому значення в круглих дужках треба ігнорувати. При обході даного гіперкуба вершина 001 обрана в якості початкової. Тут же показана нумерація каналів (0, 1, 2), по яких можливий рух при обході, а жирними лініями показаний шлях обходу згідно з правилом вибору каналу (в прямокутних дужках – номер кроку).

Рисунок 11.3 – Гіперкуби: тривимірний і чотиривимірний

Дії в алгоритмі для гіперкуба.

Для ініціатора (виконується один раз):

out (token, 1) through канал n – 1

Для кожного процесу при отриманні маркера (token, k):

begin

if k=2n then return(OK) else

begin

нехай l – найбільший номер, такий, що kmod2^l (k є дільником 2^l);

out (token, k+1) through канал l

end

end

З алгоритму видно, що рішення приймається після 2n пересилок маркера. Нехай p₀ – ініціатор, а p_k – процес, який отримує маркер (token, k). Для будь-якого k < 2n, позначення p_k і p_k+1 відрізняються на 1 біт, індекс якого позначимо як l(k), який задоволняє наступній умові:

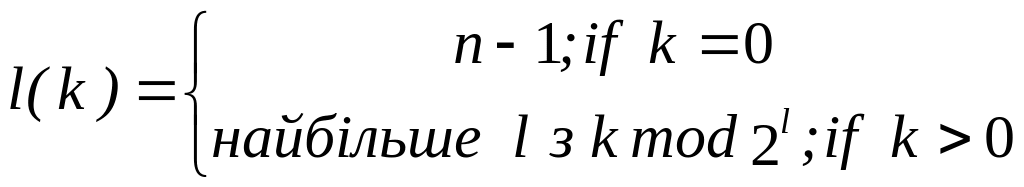
Так як для будь-якого i < n існує рівна кількість k  {0, ..., 2n} l(k) = i, то p₀ = p_2n і рішення приймається в ініціаторі. Можна показати, що з p_a = p_b випливає, що (b – a)mod2ⁿ, звідки випливає, що всі p₀, ..., p_2n-1 різні.

Алгоритм Таррі

Алгоритм обходу для довільних зв'язних графів був дан Таррі. Алгоритм заснован на наступних двох правилах.

1. Процес ніколи не передає маркер двічі по одному і тому ж каналу.

2. Не-ініціатор передає маркер своєму попереднику (сусіда, від якого він вперше отримав маркер), тільки якщо неможлива передача по інших каналах у відповідності з правилом 1.

В наступному тексті використовуються локальні змінні сайтів:

pre – сайт, що передує тому, який виконує поточний процес, тобто сайт, з якого прийшов маркер;

used[q] – ознака того, що маркер був відправлений на сайт u.

var used[q]: boolean init false для всіх u  Out(this);

pre: site init udef;

Для ініціатора (виконується один раз):

Begin

pre:=this;

u  Out(this);

used[u]:=true; out token to u;

end

Для кожного процесу при отриманні token від s:

1 begin if pre = udef then pre:= s;

2 if u  Out(this): used[u] then return(OK) /якщо всі суміжні з this вузли /

/мають ознаку true, то видається повідомлення ОК/

3 else if u  Out(this): (u  pre & used[u])

4 then begin вибір u  Out(this) \{pre}з used[u]; /вибір із вузлів, що/

/залишилися/

5 used[u]:= true; out to u token

6 end

7 else begin used[pre]:= true;

8 out token to pre

9 end

10 end

Так як процес кожного сайту передає маркер через кожний канал не більше одного разу, то кожен процес одержує маркер через кожний канал не більше одного разу. Кожен раз, коли маркер захоплюється не-ініціатором u, виходить, що процес u отримав маркер на один раз більше, ніж послав його. Звідси випливає, що кількість каналів, інцидентних u, перевищує кількість каналів, використаних u, принаймні, на 1. Таким чином, u не завершує процес, а передає маркер далі. Отже, завершення процесу проводиться сайтом-ініціатором.

Нижче показується, що при завершенні алгоритму кожен процес передав маркер.

(1) Всі канали, інцидентні ініціатору, були пройдені один раз в обох напрямках. Ініціатором маркер був посланий по всіх каналах, інакше алгоритм не завершився. Ініціатор отримав маркер рівно стільки ж разів, скільки відправив його; так як ініціатор отримував маркер кожен раз через інший канал, то маркер пересилаються через кожний канал по одному разу.

(2) Для кожного відвіданого процесу u всі канали, інцидентні u, були пройдені один разів у кожному напрямку. Припустивши, що це не так, виберемо в якості u перший процес, який зустрівся, для якого це не виконується, і зауважимо, що з пункту (1) u не є ініціатором. З вибору u, всі канали, інцидентні pre(u), були пройдені один раз в обох напрямках, звідки випливає, що u переслав маркер своєму попереднику. Отже, u використовував всі інцидентні канали, щоб переслати маркер; але, так як маркер в кінці залишається в ініціаторі, u отримав маркер рівно стільки ж разів, скільки відправив його, тобто u отримав маркер по одному разу через кожен інцидентний канал. Ми прийшли до протиріччя.

(3) Усі процеси були відвідані і кожен канал був пройдений по одному разу в обох напрямках. Якщо є невідвідані процеси, то існують сусіди u і s такі, що u був відвіданий, а s не був. Це суперечить тому, що всі канали u були пройдені в обох напрямах. Отже, з пункту (2), всі процеси були відвідані і всі канали пройдені один раз в обох напрямках.

Кожне обчислення алгоритму Таррі визначає остовне дерево графа. У корені дерева знаходиться ініціатор, а кожен не-ініціатор u наприкінці обчислення заніс свого попередника в дереві в змінну pre.