
2.4 Результаты и график
Находим точное значение интеграла, используя первообразную.
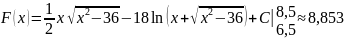
Находим численное значение интеграла для n = 10, используя метод трапеций и метод Симпсона. Программная реализация в Pascal.
program rrr;
uses crt;
var a,b,h,x,y,n,I,I01,I02,I0,y1,I1:real;
k,l:integer;
function f1 (x:real):real;
begin
f1:=sqrt(x*x-36);
end;
begin
clrscr;
write('vvedite nizhnyiu granicy a=');
readln(a);
write('vvedite verhnyiu granicy b=');
readln(b);
write('vvedite wag h=');
readln(h);
writeln('kol-vo wagov posle zapiatoi l=');
readln(l);
writeln(a,b,h,l);
I01:=0.5*b*sqrt(b*b-36)-18*Ln(sqrt(b*b-36)+b);
I02:=0.5*a*sqrt(a*a-36)-18*Ln(sqrt(a*a-36)+a);
I0:=I01-I02;
writeln('I0=',I0:1:l);
x:=a+h;
n:=b-h;
k:=0;
y:=0;
while(x<=n) do
begin k:=k+1;
if(k mod 2=0)then y:=y+2*f1(x) else y:=y+4*f1(x);
x:=x+h;
end;
y:=y+f1(a)+f1(b);
I:=(h/3)*(y);
 writeln('I=',I:1:l);
writeln('I=',I:1:l);
y1:=0;
x:=a+h;
n:=b-h;
begin
while(x<=n) do
begin
y1:=y1+2*f1(x);
x:=x+h;
end;
y1:=y1+f1(a)+f1(b);
I1:=(h/2)*y1;
writeln('I1=',I1:1:l);
end;
readln;
end.
x |
f(x) |
|
Вычисления в MathCad |
|
||
6,5 |
2,5 |
|
S |
|
|
|
6,6 |
2,749545 |
|
8,853 |
|
|
|
6,7 |
2,98161 |
|
|
|
|
|
6,8 |
3,2 |
|
Вычисления в Pascal |
|
||
6,9 |
3,407345 |
|
Метод Симпсона |
Погрешность, % |
||
7 |
3,605551 |
|
S |
|
0 |
|
7,1 |
3,796051 |
|
8,853 |
|
|
|
7,2 |
3,97995 |
|
|
|
|
|
7,3 |
4,158125 |
|
Метод Трапеций |
Погрешность, % |
||
7,4 |
4,331282 |
|
S |
|
0 |
|
7,5 |
4,5 |
|
8,853 |
|
|
|
7,6 |
4,664762 |
|
|
|
|
|
7,7 |
4,825971 |
|
|
|
|
|
7,8 |
4,983974 |
|
|
|
|
|
7,9 |
5,139066 |
|
|
|
|
|
8 |
5,291503 |
|
|
|
|
|
8,1 |
5,441507 |
|
|
|
|
|
8,2 |
5,589275 |
|
|
|
|
|
8,3 |
5,73498 |
|
|
|
|
|
8,4 |
5,878775 |
|
|
|
|
|
8,5 |
6,020797 |
|
|
|
|
|
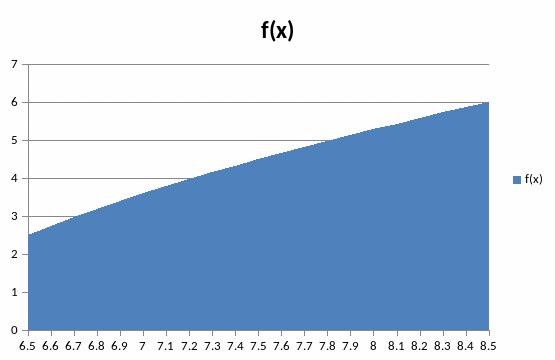
S=((2.5+6,02)/2)*2=8,852
