

Эта сетка обладает рядом замечательных свойств. Так, если функция f(x) обладает непрерывной первой производной, то интерполяционный процесс на чебышевской сетке всегда сходится. Эта сетка также позволяет: - построить интерполяционный полином близкий к полиному наилучшего равномерного приближения и - обеспечивает, в сравнении с равномерной сеткой, существенно более высокую устойчивость полинома к погрешностям задания исходных данных. Однако, следует иметь в виду, что достоинства этой сетки не предопределяют абсолютную целесообразность её использования. Это связано с тем, что: - она может оказаться не всегда удобной для вычисления соответствующих значений функции f(x) - сходимость интерполяционного процесса может потребовать построения другой сетки. В общем случае, для каждой функции существует своя система сеток, на которых интерполяционный процесс сходится. |
1.1 Метод неопределенных коэффициентов построения интерполяционного полинома
Наиболее очевидным алгоритмом построения многочлена P(x) является нахождение его коэффициентов ai из системы уравнений |
||
|
|
(4) |
Поскольку матрица этой системы уравнений |
||
|
|
(5) |
является матрицей Вандермонда и её определитель, при не совпадающих xi , не равен нулю, то система ( 4 ) имеет решение и оно единственно. Отметим, что вычисление коэффициентов полинома посредством решения системы (4) в вычислительной практике используется крайне редко. Причиной этого является плохая обусловленность матрицы (5), приводящая к заметному росту погрешности в выполнении условий интерполирования уже при сравнительно невысоких порядках полинома. К этому следует добавить, что вычислительные затраты реализации метода пропорциональны n3. Алгоритмы Ньютона и Лагранжа более устойчивы к ошибкам округления и менее трудоемки. |
||
1.2 Интерполяционный полином в форме Ньютона
Интерполяционный многочлен легко определяется если его построить в виде: |
||
|
Pn(x) = С0 + С1(x - x0) + C2(x - x0) (x - x1) + ...+ Cn(x - x0)(x - x1) ... (x - xn-1) |
(5) |
Исходя из условия интерполяции (1) для коэффициентов Ci получим систему уравнений треугольного вида |
||
|
f(x0) = С0 f(x1) = С0 + С1(x1 - x0 ) f(x2) = С0 + С1(x1 - x0 ) + C2(x2 - x0 )(x2 - x1 ) . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . f(xn ) = С0 + С1(xn - x0) + C2(xn - x0)(xn - x1) + ...+ Cn(xn - x0)(xn - x1) ... (xn- xn-1) |
|
Из этой системы легко находятся: |
||
|
|
|
Величины, стоящие в правой части приведённых выше равенств, получили название разделённых разностей, соответственно, нулевого, первого и второго порядков. Для них приняты обозначения f[xi], f[xi ,xi-1], f[xi ,xi-1 ,xi-2] и т.д. С учётом этих обозначений выражение (5) можно переписать в виде: |
||
|
Pn(x) = f[x0] + f[x1 ,x0](x - x0) + f[x2 ,x1 ,x0](x - x0)(x - x1) + ... + f[xn ,xn-1 ,...x0](x - x0)(x - x1)...(x - xn-1) |
(6) |
Можно показать, что |
||
|
|
(7) |
Выражения (6) и (7) определяют интерполяционный полином в форме Ньютона. Вычисление полинома в Ньютоновской форме удобно при последовательном дополнении сетки (n+2)-м узлом и наращивании порядка интерполяционного полинома. При этом необходимо вычислить лишь одно дополнительное слагаемое f[xn+1 ,xn,...x0](x - x0)(x - x1)...(x - xn) в выражении (6). |
||


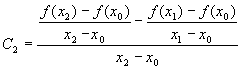 и
так далее.
и
так далее.