
Вопросы учебной программы
1. Основные понятия математической логики.
2. Логические операции над высказываниями
3. Метод математической индукции. Разложение рациональных дробей.
4. Понятие комплексного числа. Действия над комплексными числами.
5. Понятие комплексного числа. Представление комплексного числа в
тригонометрической и показательной форме.
6. Матрицы и действия над ними. Определение матрицы. Матрица-строка,
матрица-столбец, квадратная матрица, единичная матрица. Порядок матрицы.
7. Матрицы и действия над ними. Сумма матриц, разность матриц, произведение
матриц.
8. Определители матриц и их свойства.
9. Обратная матрица.
10. Решение систем линейных уравнений по формулам Крамера, методом Гаусса.
11. Алгебраические линии первого порядка. Прямая линия на плоскости.
Уравнение прямой, имеющей угловой коэффициент и проходящей через
данную точку; уравнение прямой, проходящей через две данные точки;
уравнение прямой в отрезках; общее уравнение прямой. Формула расстояния от
точки до прямой.
12. Алгебраические линии второго порядка. Окружность. Каноническое уравнение
окружности. Общее уравнение окружности.
13. Алгебраические линии второго порядка. Эллипс. Каноническое уравнение
эллипса.
14. Алгебраические линии второго порядка. Гипербола. Парабола.
15. Предел функции. Свойства предела функции. Важные пределы. Раскрытие
неопределённости (0/0) и (∞/∞).
16. Производная функции. Основные правила дифференцирования.
17. Производная функции. Производные тригонометрических функций.
18. Производная сложной функции.
19. Дифференциал функции.
20. Первообразная и неопределённый интеграл. Свойства неопределённого
интеграла.
21. Неопределённый интеграл. Методы интегрирования: непосредственное
интегрирование; интегрирование подстановкой; интегрирование по частям.
22. Определённый интеграл. Основные понятия и определения.
23. Определённый интеграл. Методы вычисления определённого интеграла.
24. Дифференциальные уравнения, основные понятия и определения.
25. Дифференциальные уравнения. Методы решения различных
дифференциальных уравнений.
26. Числовые ряды. Основные понятия и определения. Сходимость числовых
рядов.
27. Функциональные ряды, основные понятия и определения. Ряды Тейлора,
Маклорена.
28. Тригонометрические ряды, основные понятия и определения. Ряды Фурье.
29. Элементы теории вероятностей и математической статистики. Определения
понятия вероятностей.
30. Элементы теории вероятностей и математической статистики. Формула
полной вероятности. Формула Бейеса. Формула Бернулли.
Контрольная работа
Задание 1
Найти
X
из матричного уравнения:
 ,
если:
,
если:
1.1.
 .
1.2.
.
1.2.
 .
.
1.3
 .
1.4
.
1.4
 .
.
1.5
 .
1.6
.
1.6
 .
.
1.7
 1.8
1.8
 .
.
1.9
 .
1.10
.
1.10
 .
.
1.11
 .
1.12.
.
1.12.
 .
.
1.13
 1.14
1.14 .
.
1.15
 .
1.16
.
1.16

1.17
![]() 1.18
1.18

1.19
 .
1.20
.
1.20

Задание2
Вычислить комплексное число. Ответ записать в алгебраической
форме.
-
2.1

2.11

2.2

2.12

2.3

2.13

2.4

2.14


2.5

2.15

2.6

2.16

2.7

2.17

2.8
2.18

2.9

2.19

2.10

2.20

Задание 3
Решить систему линейных алгебраических уравнений двумя способами:
1) по формулам Крамера; 2) методом Гаусса.
3.1 |
|
|
3.2 |
|
|
3.3 |
|
|
3.4 |
|
|
3.5 |
|
|
3.6 |
|
|
3.7 |
|
|
3.8 |
|
|
3.9 |
|
|
3.10 |
|
|
3.11 |
|
|
3.12 |
|
|
3.13 |
|
|
3.14 |
|
|
3.15 |
|
|
3.16
|
|
|
3.17 |
|
|
3.18
|
|
|
3.19 |
|
|
3.20 |
|
|
Задание 4
Даны вершины треугольника АВС. Найти: а) уравнение стороны (АВ); б) уравнение высоты (СН); в) уравнение медианы (АМ); г) точку пересечения медианы (АМ) и высоты (СН); д) расстояние от точки С до прямой (АВ).
Вар. |
4.1 |
4.2 |
4.3 |
4.4 |
4.5 |
4.6 |
4.7 |
4.8 |
4.9 |
4.10 |
А |
(-7;-2) |
(4;-4) |
(-4;-2) |
(0;2) |
(4;-3) |
(-4;2) |
(-3;-2) |
(-2;4) |
(1;7) |
(1;0) |
В |
(3;-8) |
(8;2) |
(8;-6) |
(4;-4) |
(7;3) |
(6;-4) |
(14;4) |
(3;1) |
(-3;-1) |
(-1;4) |
С |
(-4;6) |
(3;8) |
(2;6) |
(3;2) |
(1;-16) |
(4;10) |
(6;8) |
(10;7) |
(11;-3) |
(9;5) |
|
|
|
|
|
|
|
|
|
|
|
Вар. |
4.11 |
4.12 |
4.13 |
4.14 |
4.15 |
4.16 |
4.17 |
4.18 |
4.19 |
4.20 |
А |
(4;-3) |
(-5;2) |
(3;8) |
(10;-2) |
(2;5) |
(1;-6) |
(4;-4) |
(6;-9) |
(4;1) |
(3;-1) |
В |
(7;3) |
(0;-4) |
(6;2) |
(4;-5) |
(-3;1) |
(3;4) |
(6;2) |
(10;-1) |
(-3;-1) |
(11;3) |
С |
(1;10) |
(5;7) |
(0;-5) |
(-3;1) |
(0;4) |
(-3;3) |
(-1;8) |
(-4;1) |
(7;-3) |
(-6;2) |
Задание 5.
Исследовать
сходимость числовых рядов

Вар. |
а) un |
б) un |
Вар. |
а) un |
б) un |
||
5.1. |
|
|
5.2 |
|
|
||
5.3 |
|
|
5.4 |
|
|
||
5.5 |
|
|
5.6 |
|
|
||
5.7 |
|
|
5.8 |
|
|
||
5.9 |
|
|
5.10 |
|
|
||
5.11 |
|
|
5.12 |
|
|
||
5.13 |
|
|
5.14 |
|
|
||
5.15 |
|
|
5.16 |
|
|
||
5.17 |
|
|
5.18 |
|
|
||
5.19 |
|
|
5.20 |
|
|
||
Задание 6
Найти неопределенные интегралы следующих функций:
6.1. |
а)
|
б)
|
6.2. |
а)
|
б)
|
6.3. |
а)
|
б)
|
6.4. |
а)
|
б)
|
6.5. |
а)
|
б)
|
6.6. |
а)
|
б)
|
6.7. |
а)
|
б)
|
6.8. |
а)
|
б)
|
6.9. |
а)
|
б)
|
6.10 |
а)
|
б)
|
6.11 |
а)
|
б)
|
6.12 |
а)
|
б)
|
6.13 |
а)
|
б)
|
6.14 |
а)
|
б)
|
6.15 |
а)
|
б) |
6.16
|
а)
|
б)
|
6.17 |
а)
|
б)
|
6.18 |
а)
|
б)
|
6.19 |
а)
|
б) |
6.20 |
а)
|
б)
|
Задание 7
Вычислить площадь фигуры, ограниченной параболой у=ах2+bх+с и прямой у=kх+b. Сделать чертеж.
№ варианта |
a |
b |
c |
k |
d |
№ варианта |
a |
b |
c |
k |
d |
7.01 |
1 |
4 |
2 |
1 |
6 |
7.02 |
1 |
4 |
5 |
2 |
8 |
7.03 |
1 |
4 |
8 |
3 |
10 |
7.04 |
1 |
6 |
1 |
4 |
4 |
7.05 |
1 |
6 |
4 |
5 |
6 |
7.06 |
1 |
8 |
7 |
6 |
10 |
7.07 |
1 |
8 |
0 |
7 |
2 |
7.08 |
1 |
2 |
3 |
8 |
-2 |
7.09 |
1 |
2 |
6 |
9 |
-4 |
7.10 |
2 |
2 |
9 |
10 |
3 |
7.11 |
2 |
2 |
2 |
1 |
5 |
7.12 |
2 |
4 |
5 |
2 |
17 |
7.13 |
2 |
4 |
8 |
3 |
11 |
7.14 |
2 |
6 |
1 |
4 |
5 |
7.15 |
2 |
6 |
4 |
5 |
5 |
7.16 |
3 |
2 |
2 |
1 |
4 |
7.17 |
2 |
2 |
9 |
10 |
19 |
7.18 |
2 |
8 |
0 |
7 |
3 |
7.19 |
3 |
2 |
3 |
8 |
12 |
7.20 |
3 |
4 |
5 |
2 |
6 |
Задание 8. Найти пределы функций:
8.1 |
а)
|
б)
|
8.2 |
а)
|
б)
|
8.3 |
а)
|
б) |
8.4 |
а)
|
б)
|
8.5 |
а)
|
б) |
8.6 |
а)
|
б) |
8.7 |
а)
|
б) |
8.8 |
а)
|
б)
|
8.9 |
а) |
б) |
8.10 |
а)
|
б)
|
8.11 |
А)
|
Б) |
8.12 |
А)
|
Б) |
8.13 |
а)
|
б) |
8.14 |
а)
|
б) |
8.15 |
а)
|
б) |
8.16 |
а) |
б) |
8.17 |
а) |
б) |
8.18 |
а) |
б) |
8.19 |
а) |
б) |
8.20 |
а) |
б) |
Задание 9
Найти
производную
 следующих функций:
следующих функций:
9.1. |
а)
|
|
|
|
б)
|
в)
|
|
9.2 |
а)
|
|
|
|
б)
|
в)
|
|
9.3. |
а)
|
|
|
|
б)
|
в)
|
|
9.4. |
а)
|
|
|
|
б) |
в)
|
|
9.5. |
а)
|
|
|
|
б)
|
в)
|
|
9.6. |
а)
|
|
|
|
б)
|
в)
|
|
9.7. |
а)
|
|
|
|
б)
|
в)
|
|
9.8. |
а)
|
|
|
|
б)
|
в)
|
|
9.9 |
а)
|
|
|
|
б)
|
в)
|
|
9.10 |
а)
|
|
|
|
б)
|
в)
|
|
9.11 |
а)
|
|
|
|
б)
|
в) |
|
9.12 |
а)
|
|
|
|
б) |
в)
|
|
9.13 |
а)
|
|
|
|
б) |
в)
|
|
9.14 |
а)
|
|
|
|
б)
|
в)
|
|
9.15 |
а)
|
|
|
|
б)
|
в)
|
|
9.16 |
а)
|
|
|
|
б)
|
в)
|
|
9.17 |
а)
|
|
|
|
б)
|
в)
|
|
9.18 |
а)
|
|
|
|
б)
|
в)
|
|
9.19 |
а)
|
|
|
|
б)
|
в)
|
|
9.20 |
а)
|
|
|
|
б)
|
в)
|
|
Задание 10. Найти общее и частное решение следующих дифференциальных уравнений первого порядка:
Вар. |
|
10.1. |
|
10.2 |
|
10.3 |
|
10.4 |
|
10.5 |
|
10.6 |
|
10.7 |
|
10.8 |
|
10.9 |
|
10.10 |
|
10.11 |
|
10.12 |
|
10.13 |
y(3)=3
|
10.14 |
|
10.15 |
y(3)=5 |
10.16 |
|
10.17 |
y(2)=1 |
10.18 |
y(3)=2
|
10.19 |
y(3)=3
|
10.20 |
|
Решение типового варианта контрольной работы
Задание 1
Найти ![]() ,
если
,
если ![]() ,
, ![]()
![]()
![]()
Ответ:
![]()
Задание 2
Алгебраическая форма комплексных чисел :
![]()
где i - мнимая единица; a - действительная часть: bi - мнимая часть
Действия над комплексными числами :
Если
![]() то:
то:

Пример. Выполнить действия:
а)
(2 + 3i)2;
б) (3 – 5i)2;
в) (5 + 3i)3;

Решение.
а)
(2 + 3i)2
= 4 + 2*2*3i
+ 9i2
= 4 + 12i
– 9 = – 5 + 12i;
б)
(3 – 5i)2
= 9 – 2*3*5i
+ 25i2
= 9 – 30i
– 25 = – 16 – 30i;
в)
(5 + 3i)3
= 125 + 3*25*3i
+ 3*5*9i2
+ 27i3;
так
как
i2
= – 1, а
i3
= – i,
то
получим
(5 + 3i)3
= 125 + 225i
– 135 – – 27i
= – 10 + 198i.

Задание 3
Решить
систему линейных алгебраических
уравнений
двумя способами: 1) по формулам Крамера;
2) методом Гаусса.
Решение: 1) По формулам Крамера решение системы находим в виде
 ,
,
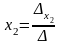 ,
,
 ,
,
где
 –
основной определитель системы, а
–
основной определитель системы, а
 –
вспомогательные определители, получаемые
из основного заменой i-го
столбца столбцом свободных членов. При
–
вспомогательные определители, получаемые
из основного заменой i-го
столбца столбцом свободных членов. При
 система имеет единственное решение.
При
система имеет единственное решение.
При
 решение следует искать другими методами.
решение следует искать другими методами.
Таким образом, имеем

 .
.
Так как , то система имеет единственное решение. Найдем вспомогательные определители:

 ,
,

 ,
,

 .
.
Тогда,
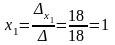 ,
,
 ,
,
 .
.
2) Для решения системы методом Гаусса составляется расширенная матрица системы, с которой можно проводить следующие действия:
а) все элементы какой-либо строки умножать или делить на одно и то же число;
б) к элементам какой-либо строки прибавлять соответствующие элементы другой строки, умноженные на одно и то же число.
Суть метода состоит в том, что с помощью этих преобразований, расширенная матрица сводится к треугольному или диагональному виду. Переходя обратно, от полученной матрицы к соответствующей системе, легко находим ее решение. Достоинство этого метода в том, что с его помощью можно решить любую систему линейных уравнений.
Составим расширенную матрицу данной системы и проведем преобразования:



При первом переходе, к элементам второй и третьей строк прибавляли соответствующие элементы первой строки, умноженные на –2 и –1, соответственно. В результате получили в первом столбце первый элемент равный 1, а под ней все нули.
При втором переходе, к элементам третьей строки прибавляли соответствующие элементы второй строки, умноженные на –1. В результате получили во втором столбце третий элемент равный нулю. Матрица приобрела
треугольный вид. На этом прямой ход метода Гаусса закончен и можно перейти к системе, которая легко решается: |
|
Но можно продолжить преобразования далее, получая нули и над элементами главной диагонали:



При первом переходе обратного хода метода Гаусса, элементы третьей строки разделили на 6, а затем к элементам первой и второй строк прибавляли соответствующие элементы полученной третьей строки, умноженные на –1 и 4, соответственно. В результате получили в последнем столбце последний элемент равный 1, а над ним все нули.
При втором переходе обратного хода метода Гаусса, элементы второй строки разделили на 3, а затем к элементам первой строки прибавляли соответствующие элементы полученной второй строки, умноженные на 1.
В результате
получили все элементы главной диагонали
равными 1,
а остальные элементы равные нулю.
Переходя к системе, получаем решение:

Задание 4
Даны вершины треугольника А (1; 7), В ( 3; 4) и С (-2; -3). Найти: а) уравнение стороны (АВ); б) уравнение высоты (СН); в) уравнение медианы (АМ); г) точку пересечения медианы (АМ) и высоты (СН); д) расстояние от точки С до прямой (АВ).
Сделаем схематический рисунок треугольника АВС.

а)
Уравнение стороны (АВ) запишем по формуле


Общее
уравнение прямой (АВ):

б)
Угловой коэффициент прямой (АВ) определим
из ее уравнения, записав его в виде
 ,
т.е.
,
т.е.

Тогда
угловой коэффициент прямой
 определим из условия
определим из условия

Уравнение
прямой (СН):


Общее
уравнение высоты (СН):

в) Находим координаты точки М – середины отрезка [CB]

Уравнение
медианы (АМ):


Общее
уравнение медианы (АМ):

г) Точку пересечения медианы (АМ) и высоты (СН) получим, решив систему из уравнений этих прямых:


д)
Расстояние от точки
 до прямой
до прямой
 вычисляется по формуле
вычисляется по формуле

Расстояние
от точки С (-2;-3) до прямой (АВ)


Построим в системе координат АВС, прямые (СН), (АМ), т. D.

Задание 5
Исследовать числовые ряды на сходимость.
а) |
|
б) |
|
в) |
|
Решение:
а)
Мы имеем ряд
 .
Его члены положительны и убывают. Найдем
к чему стремится его n-ый
член при стремлении n
к бесконечности:
.
Его члены положительны и убывают. Найдем
к чему стремится его n-ый
член при стремлении n
к бесконечности:
 .
.
Значит, необходимое условие сходимости ряда не выполняется и ряд расходится.
б)
Мы имеем ряд
 .
Его члены положительны и убывают. Найдем
к чему стремится его n-ый
член при стремлении n
к бесконечности:
.
Его члены положительны и убывают. Найдем
к чему стремится его n-ый
член при стремлении n
к бесконечности:
 .
.
Значит, необходимое условие сходимости ряда выполняется и ряд может как сходиться, так и расходиться.
Исследуем
данный ряд по предельному признаку
сравнения, согласно которому два ряда
сходятся или расходятся одновременно,
если
 .
Так как в числителе максимальная степень
n
равна 1,
а в знаменателе – 2,
то сравнивать будем с гармоническим
рядом
.
Так как в числителе максимальная степень
n
равна 1,
а в знаменателе – 2,
то сравнивать будем с гармоническим
рядом
 (
( ).
Найдем предел отношения общих членов
исходного и гармонического рядов при
стремлении n
к бесконечности:
).
Найдем предел отношения общих членов
исходного и гармонического рядов при
стремлении n
к бесконечности:
 .
.
Таким образом, по предельному признаку сравнения, исходный ряд и гармонический сходятся или расходятся одновременно. Так как гармонический ряд расходится, то расходится и исходный ряд.
в)
Мы имеем ряд
 .
Его члены положительны и убывают. Так
как в числителе общего члена ряда
присутствует факториал, а в знаменателе
степень, то при проверке стремления
этого члена при стремлении n
к бесконечности получим довольно сложный
предел:
.
Его члены положительны и убывают. Так
как в числителе общего члена ряда
присутствует факториал, а в знаменателе
степень, то при проверке стремления
этого члена при стремлении n
к бесконечности получим довольно сложный
предел:
 ,
,
то вычислять его не будем.
Исследуем
данный ряд на сходимость по предельному
признаку Д’Аламбера: если
 ,
то при
,
то при
 данный ряд сходится, при
данный ряд сходится, при
 –
расходится, при
–
расходится, при
 –
требуется исследовать по другим
признакам.
–
требуется исследовать по другим
признакам.
Поскольку
 ,
, ,
то
,
то

 .
.
Следовательно, данный ряд расходится.
Задание 6
При нахождении неопределенных интегралов следует использовать таблицу интегралов основных элементарных функций, свойства интегралов и формулу интегрирования по частям. Приведем некоторые формулы:
Свойства:
Формула интегрирования по частям
 или
более кратко
или
более кратко

Найти неопределенные интегралы:






Задание 7
Вычислить
площадь плоской фигуры, ограниченной
линиями
 и
и
 .
Выполнить рисунок.
.
Выполнить рисунок.
Решение: Найдем точки пересечения данных кривых:




 ,
,


 ,
,
 .
.
Используя
найденные точки
Воспользуемся
формулой вычисления площади плоской
фигуры
|
|



 .
.
Ответ:  (кв. ед.).
(кв. ед.).
Задание 8
Найти указанные пределы, не пользуясь правилом Лопиталя.
а) |
|
|
б) |
|
в) |
|
|
|
|
Решение:
а) Предел частного равен частному
пределов, если эти пределы существуют,
конечны и знаменатель не равен нулю. В
этом же примере в числителе и в знаменателе,
при подстановке вместо x
– бесконечности, получаем бесконечности.
В таких случаях говорят, что имеем
неопределенность вида  (бесконечность
делить на бесконечность). Для раскрытия
этой неопределенности целесообразно
выделить элементы, порождающие эти
бесконечности. Для этого и в числителе,
и в знаменателе вынесем за скобку степень
x
с наибольшим показателем. В результате
выражения в скобках будут стремиться
к конечным пределам, а степени x
за скобками сократятся. Решим данный
пример:
(бесконечность
делить на бесконечность). Для раскрытия
этой неопределенности целесообразно
выделить элементы, порождающие эти
бесконечности. Для этого и в числителе,
и в знаменателе вынесем за скобку степень
x
с наибольшим показателем. В результате
выражения в скобках будут стремиться
к конечным пределам, а степени x
за скобками сократятся. Решим данный
пример:

 .
.
б)
В данном случае также не можем применить
теорему о пределе частного, так как
знаменатель стремиться к нулю. В числителе
и в знаменателе при подстановке x=1
получаем нули. В таких случаях говорят,
что имеем неопределенность вида  (ноль
делить на ноль). Для раскрытия этой
неопределенности целесообразно выделить
элементы, порождающие нули (возможно,
это будут множители вида (x–1)).
Для этого и числитель, и знаменатель
разложим на множители:
(ноль
делить на ноль). Для раскрытия этой
неопределенности целесообразно выделить
элементы, порождающие нули (возможно,
это будут множители вида (x–1)).
Для этого и числитель, и знаменатель
разложим на множители:
 ,
,
 .
.
Подставляя соответствующие выражения и сокращая общий множитель (x–1), стремящийся к нулю, но не равный ему, получим
 .
.
в)
В числителе и в знаменателе при подстановке
x=0
получаем нули. Имеем неопределенность
вида
.
Так как в примере присутствуют
тригонометрические функции, то для
раскрытия неопределенности можно
применить первый замечательный предел:
 .
Преобразуем выражение под знаком
предела, используя тригонометрические
формулы:
.
Преобразуем выражение под знаком
предела, используя тригонометрические
формулы:


 ,
так как
,
так как
 и
.
и
.
Задание 9
При нахождении производной заданных функций следует пользоваться таблицей производных основных элементарных функций, правилами дифференцирования и теоремой о дифференцировании сложной функции. Приведем некоторые формулы:
1.
|
6.
|
2.
|
7.
|
3.
|
8.
|
4.
|
9.
|
5.
|
10.
|
Правила дифференцирования:
Если
 т.е.
т.е.
 - сложная функция, то
- сложная функция, то

Примеры
Найти :
а)



б)


в)


г)


д)


Задание 10
Дифференциальное
уравнение (ДУ) первого
порядка имеет вид
 или
или
 где
где
 у
– искомая функция от переменной х,
у
– искомая функция от переменной х,
 .
.
Процесс решения ДУ называется его интегрированием.
ДУ с разделяющимися переменными имеет вид
 (1)
(1)
Пусть
 и
и
 Разделим обе части уравнения (1) на
произведение
Разделим обе части уравнения (1) на
произведение
 получим ДУ
с разделенными переменными
получим ДУ
с разделенными переменными
 (2)
(2)
Равенство (2) означает, что дифференциалы двух функций равны,, значит сами функции отличаются лишь на постоянное слагаемое. Интегрируя равенство (2), получим общее решение или общий интеграл ДУ (1)

Пример: Проинтегрировать ДУ

Разделим переменные и проинтегрируем обе части равенства

 -
общий интеграл
исходного ДУ, где
-
общий интеграл
исходного ДУ, где




















































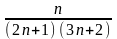




 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
; ;
;
 ;
;
 ;
;
 ;
; ;
;













































































 y(2)=1
y(2)=1 y(2)=4
y(2)=4 y(1)=5
y(1)=5 y(1)=3
y(1)=3 y(3)=2
y(3)=2 y(1)=3
y(1)=3 y(2)=5
y(2)=5
 y(3)=1
y(3)=1 y(1)=2
y(1)=2



 ;
; ;
; ;
;













 и
и
 ,
построим фигуру, ограниченную линиями:
,
построим фигуру, ограниченную линиями: –
парабола с
вершиной
–
парабола с
вершиной
 и
и
 –
прямая.
–
прямая. ,
где
,
где
 –
уравнение верхней, а
–
уравнение верхней, а
 –
нижней границы области. В нашем
случае, так как
–
нижней границы области. В нашем
случае, так как
 и
и
 ,
то
,
то
 ;
; ;
; ;
;





 ,
,
 ,
,




