
- •Уджсикасö велöдан канму учреждение
- •Содержание
- •Введение
- •Общие методические рекомендации
- •Уджсикасö велöдан канму учреждение
- •Уджсикасö велöдан канму учреждение
- •Тематический план по дисциплине Математика
- •Учебная литература
- •2. Н.В. Богомолов, п.И. Самойленко Математика. - м.: Дрофа, 2004
- •Варианты контрольной работы
Учебная литература
Основные источники:
Богомолов Н.В. Практические занятия по математике. - М.: Дрофа- 2010.- 400 с.
Богомолов Н.В., Сергиенко Л.Ю. Сборник дидактических заданий по математике. - М.-Дрофа-2009
Григорьев С.Г. Математика: учебник для студентов сред.проф. учреждений / С.Г.
Григорьев, С.В. Задулина; под ред. В.А. Гусева. - 2-е изд., стер. - М.: Издательский центр «Академия», 2007. - 384 с.
Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. - 4-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2010. - 573 с.
Спирина М.С. Теория вероятностей и математическая статистика: учебник для студ. учреждений сред.проф. образования / М.С. Спирина, П.А. Спирин. - М.: Издательский центр «Академия», 2007. - 352 с.
Спирина М.С. Дискретная математика: учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. -М.: Издательский центр «Академия», 2010. - 368 с.
П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова Высшая математика в упражнениях и задачах. Часть 1 и 2. - М.: Высшая школа, 2008.
М.Я. Выгодский Справочник по высшей математике. - М.: Росткнига, 2001.
А.А. Дадаян, Математика: /А.А. Дадаян. -2 изд. –М. : Форум, 2010
А.А. Дадаян, Сборник задач по математике: учебное пособие /А.А. Дадаян–М. : Форум:Инфа-М, 2008.
Дополнительные источники:
1. Н.В. Богомолов Задачи по математике с решениями. - М.: Высшая школа, 2006
2. Н.В. Богомолов, п.И. Самойленко Математика. - м.: Дрофа, 2004
3. З.И. Гурова, С.Н. Каролинская, А.П. Осипова Математический анализ. Начальный курс с примерами и задачами- М.: ФИЗМАТ ЛИТ, 2002
4. И. Д. Пехлецкий Математика. - М.: Мастерство, 2001
5. В.Ф. Бутузов, Н.И. Крутицкая. Математичесий анализ в вопросах и задачах. - М.: Физматлит, 2000
Интернет - ресурсы:
Единое окно доступа к образовательным ресурсам. Электронная библиотека [Электронный ресурс]. — Режим доступа: http://window.edu.ru/window,свободный. — Загл. с экрана.
Российская национальная библиотека [Электронный ресурс]. — Режим доступа: http:// nlr.ru/lawcenter, свободный. — Загл. с экрана.
Электронные библиотеки России/pdfучебники студентам [Электронный ресурс].— Режим доступа:
http://www.gaudeamus.omskcitv.com/mvPDFlibrary.html,свободный.—Загл. с экрана
Варианты контрольной работы
x/y |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 11 21 31 41 51 61 |
2 12 22 32 42 52 62 |
3 13 23 33 43 53 63 |
4 14 24 34 44 54 64 |
5 15 25 35 45 55 65 |
6 16 26 36 46 56 66 |
7 17 27 37 47 57 67 |
8 18 28 38 48 58 68 |
9 19 29 39 49 59 69 |
10 20 30 40 50 60 70 |
1 |
2 11 24 36 45 59 66 |
3 12 25 31 47 52 69 |
4 20 27 34 41 57 62 |
5 17 21 38 49 51 65 |
6 13 23 35 43 56 67 |
7 19 26 32 50 54 63 |
8 16 30 39 44 53 64 |
9 14 29 40 48 55 68 |
10 18 22 37 46 58 70 |
1 15 28 33 42 60 61 |
2 |
3 20 27 31 49 54 62 |
4 11 29 40 43 60 65 |
5 18 25 37 44 51 66 |
6 15 22 34 50 56 67 |
7 12 28 35 41 59 64 |
8 19 30 56 47 57 61 |
9 16 30 37 42 55 68 |
10 13 24 33 48 58 69 |
1 17 26 32 45 53 70 |
2 14 21 36 48 52 63 |
3 |
4 14 28 35 41 59 64 |
5 17 21 34 48 57 62 |
6 12 30 39 44 53 69 |
7 19 24 38 46 52 70 |
8 15 27 33 42 60 61 |
9 11 22 31 45 56 65 |
10 20 23 36 43 58 67 |
1 16 29 40 47 55 68 |
2 13 26 32 50 54 63 |
3 18 25 37 49 51 66 |
4 |
5 12 23 36 43 59 62 |
6 18 25 37 44 55 66 |
7 14 28 35 50 56 61 |
8 13 24 31 48 58 69 |
9 20 26 32 50 54 63 |
10 16 30 33 41 57 68 |
1 15 22 34 45 53 67 |
2 17 21 38 49 51 65 |
3 11 29 40 47 60 64 |
4 19 27 39 46 52 70 |
5 |
6 17 21 34 48 57 62 |
7 19 28 39 44 51 64 |
8 15 30 36 47 60 61 |
9 11 26 32 50 54 65 |
10 14 23 37 41 52 63 |
1 18 24 31 45 58 69 |
2 13 29 40 49 55 66 |
3 20 22 38 42 59 70 |
4 16 27 35 43 56 68 |
5 12 25 33 46 53 67 |
6 |
7 13 29 40 47 55 68 |
8 15 25 37 44 58 66 |
9 18 23 35 41 54 62 |
10 12 24 31 48 52 69 |
1 16 21 36 43 57 65 |
2 19 27 33 42 60 61 |
3 17 26 39 46 51 70 |
4 11 30 32 50 53 67 |
5 14 22 38 45 59 64 |
6 20 28 34 49 56 63 |
7 |
8 19 28 35 50 53 61 |
9 13 21 33 45 60 68 |
10 11 29 40 43 57 65 |
1 14 30 36 47 55 69 |
2 20 25 39 44 51 64 |
3 17 26 32 46 54 70 |
4 15 22 38 42 59 62 |
5 18 24 31 48 52 66 |
6 12 27 34 41 56 67 |
7 16 23 37 49 58 63 |
8 |
9 16 21 35 48 60 61 |
10 14 27 33 41 53 65 |
1 18 29 31 44 58 66 |
2 17 30 37 42 55 68 |
3 11 28 34 45 51 64 |
4 20 26 32 50 54 62 |
5 12 25 40 46 57 69 |
6 15 23 36 49 56 63 |
7 19 24 38 43 52 70 |
8 13 22 39 47 59 67 |
9 |
10 18 25 37 44 55 66 |
1 20 27 39 41 57 62 |
2 13 24 36 48 52 70 |
3 19 28 33 42 60 61 |
4 17 21 38 43 51 65 |
5 12 23 31 47 56 68 |
6 14 29 35 46 59 64 |
7 17 30 40 49 58 69 |
8 15 22 34 45 53 67 |
9 11 26 32 50 54 63 |
Задания
Найдите предел функции а)
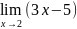 б)
б)

Найдите предел функции
а)
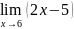 б)
б)
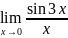
Найдите предел функции а)
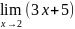 б)
б)
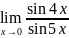
Найдите предел функции а)
 б)
б)
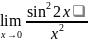
Найдите предел функции а)
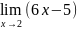 б)
б)
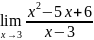
Найдите предел функции а)
 б)
б)
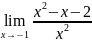
Найдите предел функции а)
 б)
б)
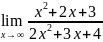
Найдите предел функции а)
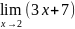 б)
б)

Найдите предел функции а)
 б)
б)
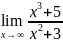
Найдите предел функции а)
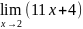 б)
б)
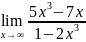
Найдите неопределенный интеграл a)
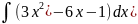 б)
б)
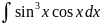
тНайдите неопределенный интеграл a)
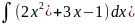 б)
б)
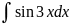 ь
ьНайдите неопределенный интеграл a)
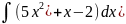 б)
б)

Найдите неопределенный интеграл a) б)
Найдите неопределенный интеграл a) б)
Найдите неопределенный интеграл a)
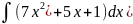
б)
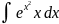
Найдите неопределенный интеграл a)
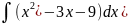
б)
 ьь
ьь
Найдите неопределенный интеграл a)

б)

Найдите неопределенный интеграл a)
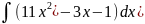
б)
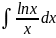
Найдите неопределенный интеграл a)
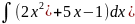 б)
б)

Вычислите определенный интеграл а)
 б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
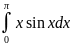
в) Вычислите площадь фигуры, ограниченной заданными линиями
Y
= 3 x- ,
y=0
,
y=0
Вычислите определенный интеграл а)
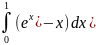 б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
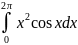
в) Вычислите площадь фигуры, ограниченной заданными линиями Y=x2, x=a, x=b, b>a
Вычислите определенный интеграл а)
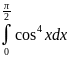 б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
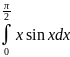 в)
Вычислите площадь фигуры, ограниченной
заданными линиями Y
= 6x
- x2,
y
= 0
в)
Вычислите площадь фигуры, ограниченной
заданными линиями Y
= 6x
- x2,
y
= 0Вычислите определенный интеграл а)

б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
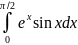
в)
Вычислите площадь фигуры, ограниченной
заданными линиями Y=sinx,
y=0,
x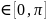
Вычислите определенный интеграл а)
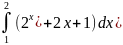
б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
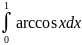
в) Вычислите площадь фигуры, ограниченной заданными линиями Y=x2-3x, y+3x-4=0
Вычислите определенный интеграл а)
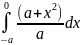
б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям

в) Вычислите площадь фигуры, ограниченной заданными линиями Y=2x, y=2, x=0
Вычислите определенный интеграл а)
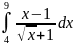
б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
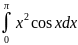
в)
Вычислите площадь фигуры, ограниченной
заданными линиями Y=
Вычислите определенный интеграл а)
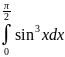
б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
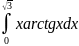
в) Вычислите площадь фигуры, ограниченной заданными линиями Y=x2, x+y=2
Вычислите определенный интеграл а)

б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
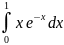
в)
Вычислите площадь фигуры, ограниченной
заданными линиями Y=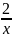 ,
y=3-x
,
y=3-x
Вычислите определенный интеграл а)
б)
Вычислите интеграл, пользуясь формулой
интегрирования по частям
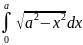
в) Вычислите площадь фигуры, ограниченной заданными линиями Y=2x, y=2, x=0
Найдите общее решение дифференциального уравнения с разделяющимися переменными а) Y =
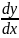 +
x
= 1
+
x
= 1Найдите общее решение дифференциального уравнения с разделяющимися переменными (xy2+x) dx + (y - x2y)
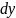 =0т
=0тНайдите общее решение дифференциального уравнения с разделяющимися переменными (1+2y)xdx+(1+x2) =0
Найдите общее решение дифференциального уравнения с разделяющимися переменными xy(1+x2)y’=1+y2
Найдите общее решение дифференциального уравнения с разделяющимися переменными Y= +y=y2
Найдите общее решение дифференциального уравнения с разделяющимися переменными (
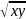 -
-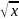 )
+ydx=0
)
+ydx=0Найдите общее решение дифференциального уравнения с разделяющимися переменными (2х3у – у4)dx + (2xy3 – x4)dy = 0
Найдите общее решение дифференциального уравнения с разделяющимися переменными (y2+xy) dx - x2 =0
Найдите общее решение дифференциального уравнения с разделяющимися переменными y(x2 + y2)dx – x3dy = 0
Найдите общее решение дифференциального уравнения с разделяющимися переменными (x2 + y2+ xy)dx – x2dy = 0
Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям (1+y2)dx - xy =0; x0=0, y0=1
Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям 2dx= ; y(0)=1
Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям (2x+1)dy+y2dx=0; y(4)=1
Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям (xy2+x)+(x2y-y)y’=0; x0=0, y0=1
Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям (1+y2)dx-xy =0; x0=1, y0=0
Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям
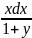 -
-
 =
0; y(1)=1
и y(0)=1
=
0; y(1)=1
и y(0)=1Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям Y’sinx=y
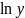 ;
y(0)=1
и y
;
y(0)=1
и y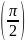 =1
=1Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям (1+ex)yy’=ex, y(1)=1
Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям x
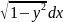 +y
+y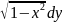 =0;
y(0)=1
=0;
y(0)=1Найдите частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям х2dу=(xу+ у2)dх ;y)= -1; х = 1
Разложить ряд Маклорена и найти интервалы сходимости функций f(x)=ax, 0<a≠1
Разложите ряд Маклорена и найдите интервалы сходимости функций f(x) =
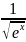
Разложить ряд Маклорена и найти интервалы сходимости функций f(x)=x2e-2x
Разложить ряд Маклорена и найти интервалы сходимости функций f(x)=sinx2
Разложить ряд Маклорена и найти интервалы сходимости функций f(x)= sin2x
Разложить ряд Маклорена и найти интервалы сходимости функций f(x)=x3cosx
Разложить ряд Маклорена и найти интервалы сходимости функций f(x)=
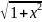
Разложить ряд Маклорена и найти интервалы сходимости функций f(x)=
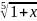
Разложить ряд Маклорена и найти интервалы сходимости функций f(x)=
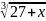
Разложить ряд Маклорена и найти интервалы сходимости функций
f(x)= ln(1+x)
Вычислите 5(cos 10
 +
i sin 10
)
+
i sin 10
)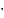 2(cos
80
+i
sin80
)
2(cos
80
+i
sin80
)Вычислите 3(cos50 +i sin 50 ) 4(cos 70 + i sin 70 ).
Вычислите 2 ( cos
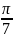 +
i sin
)
6(cos
+
i sin
)
6(cos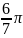 +
i sin 10
+
i sin 10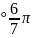 )
)Вычислите (cos
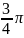 +
i sin
)
5(cos
+
i sin
)
5(cos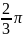 +i
sin
)
+i
sin
) 7(xos
7(xos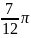 +
i sin 12
+
i sin 12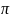 )
)Вычислите (1+
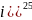
Вычислите (
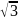 +
+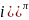
Вычислите (
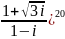
Вычислите

Вычислите
Вычислите
5(
cos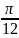 +
i sin
)
+
i sin
)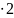 (cos
(cos +
i sin 10
+
i sin 10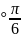 )
)
