Оценка срока службы изоляторов конденсаторного типа

В изоляторах с конденсаторными обкладками пробой одного соя изоляции влечет за собой перераспределение электрического напряжения, что вызывает довольно быстрый отказ последующих слоев изоляции. Если пренебречь временем развития разрушения, то можно принять срок службы изолятора равным сроку службы одного слоя изоляции между соседними обкладками.

В основу расчета положена методика, рассмотренная в [2].

Расчет внутренней изоляции

Расчет проводится для наиболее нагруженного слоя. Механическое напряжение в изоляции предполагается равным нулю.

1. Вероятность безотказной работы одного из слоев при равновероятном отказе любого из них

,

где Р(τ) – вероятность безотказной работы изолятора; Р_k(τ) – вероятность безотказной работы одного слоя; m – число слоев изоляции.

2. Функция распределения наибольших значений y

,

где S- площадь наиболее нагруженного слоя

η – коэффициент неравномерности поля

i – номер слоя (первый или последний).

Остальные параметры, входящие в уравнение определяют по таблице 2

Таблица 2 – Параметры уравнения «кривой жизни»

, Дж	, Дж·м/В	,
5,5·10-19	4·10-27	0.001	5	0.15	2·10-7

3. Число рядом расположенных неоднородностей y. Задаваясь рядом значений y, определяют значения функции F(y), строят зависимость F(y) и по полученному графику определяют искомое y при F(y)= Р_k(τ) (рисунок 4)

Рисунок 4 – Подбор значения y

4. Коэффициент неоднородности электроизоляционного материала

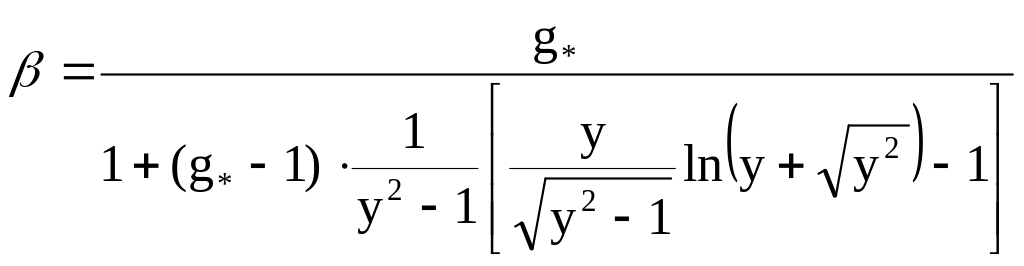
g_*- относительная проводимость неоднородности (таблица 2).

5. В эксплуатационных условиях электрическая изоляция подвергается действию постоянных, переменных и случайных нагрузок. Если старение изоляции в эксплуатации не имеет особого значения, то для расчета времени до ее отказа несущественно, в каком порядке действует нагрузка.

Так как случайные нагрузки (в данном случае перенапряжения) являются непрерывными, то их необходимо заменить дискретными следующим образом:

5.1 Определяется нижняя граница диапазона нагрузок

5.2 Определяется верхняя граница диапазона нагрузок

где k=1,2 – 1,3

5.3 Полученный диапазон разбивается на n=10 – 15 интервалов, определяются ширина

и границы U_i-1; U_i каждого интервала.

5.4 Определяется середина каждого интервала

5.5 Рассчитывается значение функции распределения вероятностей перенапряжений F(U^*_i) для нормального закона

где М(U) – математическое ожидание

- интеграл Лапласа.

Определяется приращение функции на интервале

Напряженность поля при действии перенапряжений

где = Е_rдоп - максимальная радиальная напряженность при расчетном напряжение U_р= U_{наиб.раб}

при действии рабочих напряжений

Е_i=Е_раб.

Относительное время действия перенапряжения

где N – число перенапряжений в год; - продолжительность одного перенапряжения, с; - продолжительность года, с.

Рассчитанные значения можно представить в виде таблицы 3.

Таблица 3 – Расчет случайной нагрузки

j

Ui-1, кВ

Uj ,кВ

Ui*, кВ

F(Ui*)

∆F(Ui*)

ηEi

τi/τj

6. По заданному исполнению и категории размещения по таблице 3-1 [2] выбирается диапазон рабочих температур (верхнее Т_в и нижнее Т_н значения).

7. Полученный диапазон разбивается на n=10 – 15 интервалов, определяются ширина

и границы Т_i-1; Т_i каждого интервала.

8. Определяется середина каждого интервала

9. Строится годовой график температур (рисунок 5) и определяются продолжительности действия средних температур в году (в днях и секундах).

10. Для полученных средних температур окружающей среды определяем соответствующие температуры изоляции

,

где Q_отв – определяются по графику тепловой устойчивости для точки А.

При расчете учитываются только те , для которых можно выполнить следующие построения. На оси Т_и графика тепловой устойчивости откладывается и через эту точку проводится прямая параллельная Q_отв. Если данная прямая имеет пересечение с кривой Q_и, то средняя температура окружающей среды используется при расчете температуры изоляции Т_i.

Количество полученных температур m.

Рисунок 5 – Распределение годовой температуры по месяцам

11. Рассчитанные значения можно представить в виде таблицы 4.

Таблица 4

j

Диапазон измерения

Ср. темп

Время действия T, дни

Время действия Т, сек

Ti, К при 20С

12. Определяется вероятность разрыва связи в единицу времени при действии рабочих напряжений q_i и действии перенапряжений q_ij с учетом действия температур Т_i, К

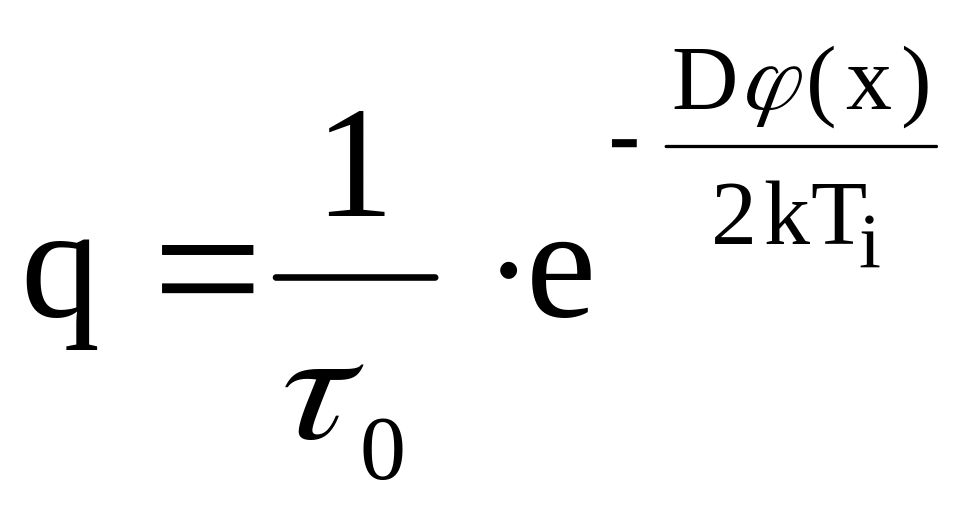
где φ(х) - функция нагрузки, действующей на связь

х - безразмерная характеристика нагрузки

13. Расчет времени до отказа

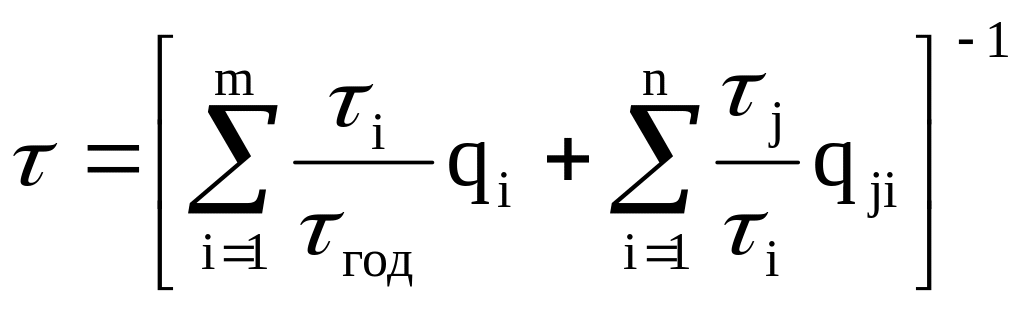
Расчет внешней изоляци

1. Вероятность пробоя изоляции при одном перенапряжении

где Q(U_пер) – функция распределения вероятностей амплитуд перенапряжений при напряжении перекрытия

Амплитудное значение напряжения перекрытия

Разбиваем промежуток ( ) на n интервалов с шагом ΔU_пер=10кВ и для каждого значения рассчитываем Q(U_перi) и f(U_перi) :

,

где М(U_пер) – математическое ожидание перекрытий

;

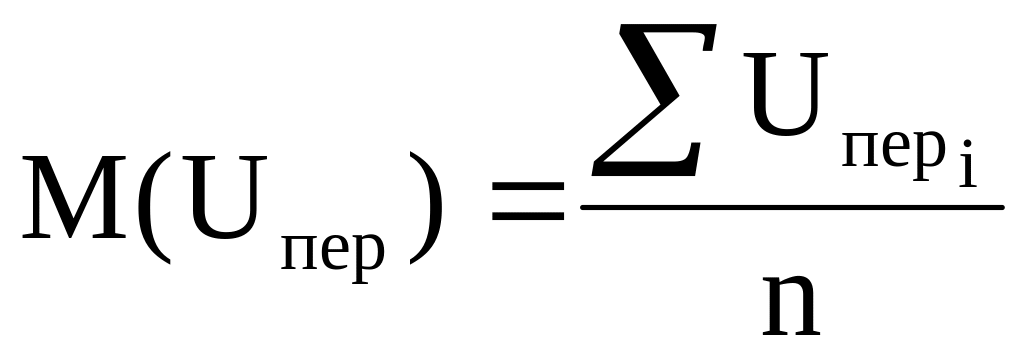σ-среднеквадратичное отклонение

f(U_пер) - функция плотности распределения вероятностей перекрытий

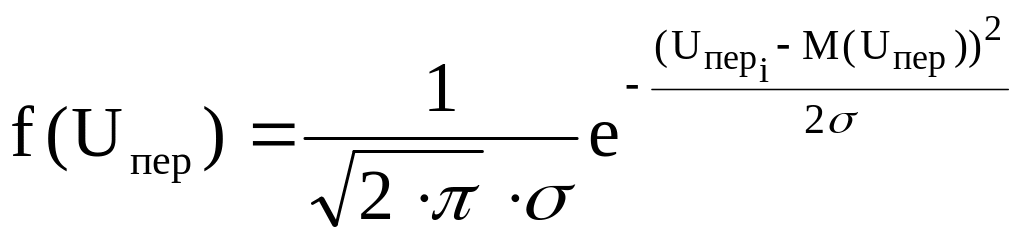
2. Вероятность отсутствия перекрытия за τ лет

3. Вероятность перехода перекрытия в дугу:

4. Вероятность разрушения изолятора дугой принимается

Тогда вероятность разрушения изолятора в результате перекрытия:

5. Вероятность безотказной работы фарфоровой покрышки:

Вероятность безотказной работы изолятора