1.7 Решение уравнения состояния в канонической форме
Найдем
решение y(t)
для системы уравнений в канонической
форме, если начальные условия имеют
вид: y(0)
= 0.1*a2
= 1.6; y'(0)
= y''(0)
= 0. Сигнал
u(t)
= a2*1(t)
= 16.
Переходя
к начальным условиям для x,
в соответствии с принятыми ранее
обозначениями получим
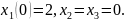 Каждое из дифференциальных уравнений
первого порядка
Каждое из дифференциальных уравнений
первого порядка 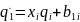 зависит
только от одной переменной и его решение
в общем виде имеет вид
зависит
только от одной переменной и его решение
в общем виде имеет вид
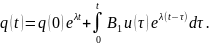
При
этом,
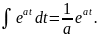
Определим
начальные условия q(0)
для вектора q(t),
так
как
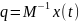 ,
то
,
то
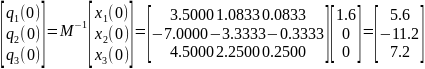 .
.
Найдем
выражения для
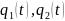 и
и
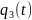 :
:
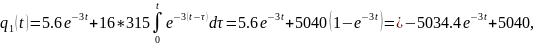
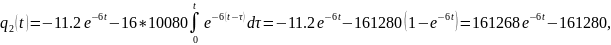
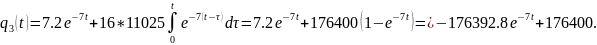
В
результате получим
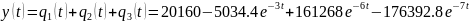 .
.
Выполним
проверку:
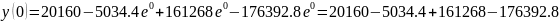
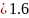 .
.
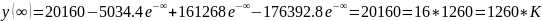 .
.
В
первом разделе курсового проекта для
заданной передаточной функции определены
временные и частотные характеристики
системы. Также функция была представлена
в трех формах: нормальной, канонической
и ss.
Для каждой из форм были построены схемы
моделирования и найден вид переходного
процесса. Из полученных графиков видно,
что для каждой из форм вид переходного
процесса одинаков, т.е. все формы
равнозначны.


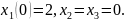 Каждое из дифференциальных уравнений
первого порядка
Каждое из дифференциальных уравнений
первого порядка 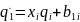 зависит
только от одной переменной и его решение
в общем виде имеет вид
зависит
только от одной переменной и его решение
в общем виде имеет вид
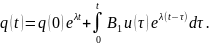
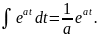
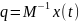 ,
то
,
то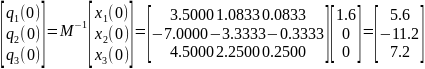 .
.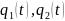 и
и
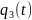 :
: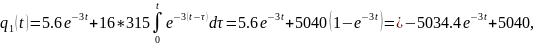
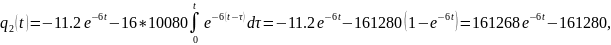
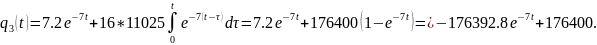
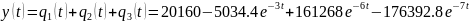 .
.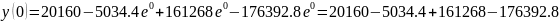
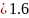 .
.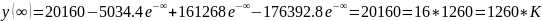 .
.