Глава 1 Математическое описание линейных систем
1.1 tf-, zpk-, ss- формы для заданной передаточной функции
tf – полиномиальная форма, в которой передаточная функция задается двумя векторами-строками, составленными из коэффициентов многочленов числителя и знаменателя в порядке убывания степеней S.
Результаты в MATLAB:
>>W = tf ([1260 2520 0], [1 16 81 126]);
Transfer function:
12620s^2+2520s
---------------------------------
s^3 + 16s^2 + 81s + 26
zpk - форма нулей, полюсов и коэффициента усиления, в которой полиномы записаны через нули числителя – zi и полюса знаменателя pj.
Результаты в MAT-LAB:
>>zpk(W)
Zero/pole/gain:
1260 s (s+2)
----------------------
(s+7) (s+6) (s+3)
ss - форма представляет передаточную функцию в параметрах пространства состояний. Система n-го порядка с одним входом и одним выходом в параметрах пространства состояний описывается системой уравнений:
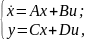
где А - матрица коэффициентов обратных связей, охватывающих все n интеграторов; B - матрица коэффициентов связей входов всех интеграторов с входом модели; C - матрица коэффициентов связей выходов всех интеграторов с выходом модели; D - матрица коэффициентов связей входов и выходов модели напрямую, минуя интеграторы.
Результаты в MATLAB:
>>ss(W)
a =
x1 x2 x3
x1 -16 -10.13 -3.938
x2 8 0 0
x3 0 4 0
b =
u1
x1 32
x2 0
x3 0
c =
x1 x2 x3
y1 39.38 9.844 0
d =
u1
y1 0
1.2 Характеристическое уравнение и его корни. Разложение передаточной функции на сумму простых слагаемых
Передаточная функция системы W(s) – это отношение изображения по Лапласу выходного сигнала Y(s) к изображению по Лапласу входного сигнала U(s) при нулевых начальных условиях.
Заданная передаточная функция:
Выражение
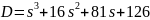называется
характеристическим полиномом системы.
Характеристический
полином является важнейшей характеристикой
модели, определяющей устойчивость
переходных процессов, их форму и
длительность.
Корни характеристического уравнения имеют вид:
Т.к. корни характеристического уравнения отрицательные, то система устойчива. Устойчивой называется система, которая после прекращения внешнего воздействия через некоторое время возвращается к тому состоянию равновесия или вынужденного движения, в котором находилась до начала воздействия.
Представим передаточную функцию в виде суммы простых слагаемых:
Найдем A, B, C
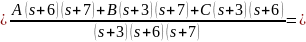
Следовательно,
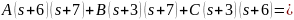
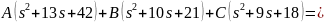
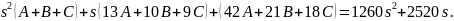
Получим систему уравнений:
В
результате решения данной системы
получим
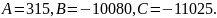
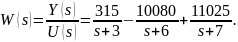
Импульсная переходная характеристика w(t) – это процесс изменения сигнала на выходе при подаче на вход δ-функции. Ее можно найти в результате обратного преобразования Лапласа, примененного к каждому слагаемому передаточной функции.
В
соответствии с таблицами соответствия
,
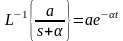тогда
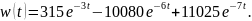
Результаты в MATLAB:
>> ch=[1260 2520 0]
ch =
1260 2520 0
>> zn=[1 16 81 126]
zn =
1 16 81 126
>> x=residue(ch,zn)
x =
1.0e+04 *
1.1025
-1.0080
0.0315
Полученные в MATLAB переменные х – коэффициенты разложения.
Переходная
характеристика h(t)
– это процесс изменения сигнала на
выходе системы при подаче на вход
единичного ступенчатого воздействия.
Преобразование по Лапласу 1(t)
эт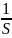о 
,
следовательно
Для получения аналитической формы переходной характеристики дополним систему интегратором:
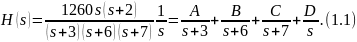
Результаты в MATLAB:
>> ch=[1260 2520 0]
ch =
1260 2520 0
>> zn=[1 16 81 126 0]
zn =
1 16 81 126 0
>> x=residue(ch,zn)
x =
-15750
16800
-1050
0
Таким образом получены коэффициенты A, B, C и D:
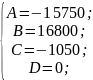
Подставив коэффициенты в формулу (1.1), получим:
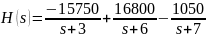
Запишем аналитическую форму переходной характеристики
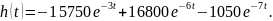
Переходную характеристику можно также вычислить следующим образом
