9. Если , , то найти

Егер , болса, жиын табылсын.

1. 

2. 

3. 

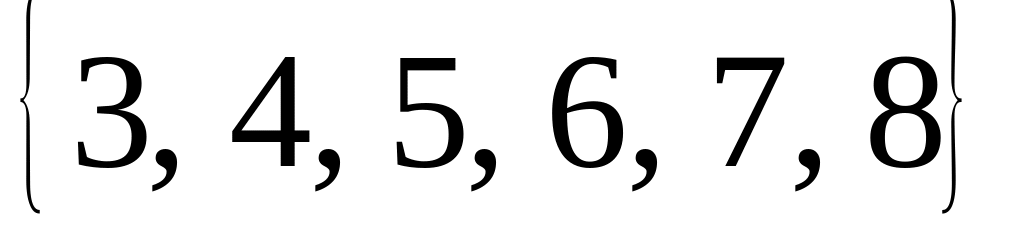
4. Ø

5. 

10. Если , , то найти

Егер , , болса, жиын табылсын.

1. 

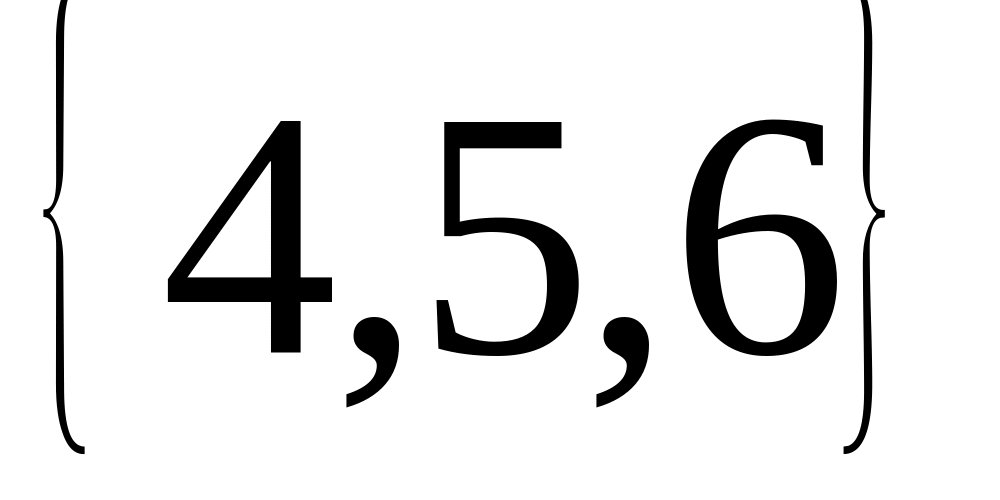
4. Ø

$$6$$

1.

1. 

2. 

3. 

4. 

5. 

2.

3.

4.

1. 

5.

1. 

3. 

6.

1. 

2. 

3. 

7. 7 құжаттан қанша тәсілмен 3 құжатты таңдап алуға болады?

1. 35

2. 7!

3. (7-3)!

4. 3!

5. 350

8. 3,4,5,7 төрт цифрмен жасалатын барлық үш таңбалы сандар нешеу болады?

1. 64

2. 6!

3. 28

4. 16

5. 36

1. Барлық бес таңбалы сан нешеу?

1. 90 000

2. 900 000

3. 990 000

4. 99 000

5. 9000

10. Сөзде әріптер: а - 4 рет , б - 4 рет , в - 2 рет және г – 2 рет қайталанып , ол сөз барлығы 12 әріптен құралған. Осы әріптермен барлығы 12 әріпті неше сөз жазуға болады?

1. 207900

2. 27900

3. 7900

4. 20900

5. 20790

$$7$$

1.

1. 10

2. 7

3. 20

4. 100

5. 30

2.

1. 10

2. 7

3. 20

4. 100

5. 30

3.

1. 1

2. 10

3. 25

4. 120

5. 0

4.

1. 120

2. 1

3. 10

4. 25

5. 0

5.

1. 6

2. 11

3. 30

4. 720

5. 1

6.

1. 6

2. 11

3. 30

4. 720

5. 1

7.

1. 15

2. 12

3. 36

4. 30

5. 4

8.

1. 20

2. 15

3. 120

4. 18

5. 3

9.

1. 15

2. 12

3. 36

4. 30

5. 4

10.

1. 1

2. 0

3. 12

4. 36

5. 720

$$8$$

1.

1. 720

2. 0

3. 120

4. 36

5. 1

2.

1. 9

2. 8

3. 6

4. 1

5. 5

3.

1. 27

2. 9

3. 6

4. 0

5. 1

4.

1. 8

2. 9

3. 1

4. 0

5. 6

5.

1. 16

2. 8

3. 6

4. 2

5. 12

6.

1. 16

2. 8

3. 6

4. 2

5. 12

7.

1. 81

2. 64

3. 4

4. 12

5. 24

8.

1. 64

2. 81

3. 4

4. 12

5. 24

9.

1. 256

2. 16

3. 24

4. 1

5. 0

10.

1. 125

2. 243

3. 15

4. 60

5. 30

$$9$$

1.

1. 243

2. 125

3. 60

4. 15

5. 30

2.

1. 25

2. 32

3. 10

4. 20

5. 60

3.

1. 4

2. 2

3. 1

4. 0

5. 3

4.

1. 15

2. 6

3. 7

4. 12

5. 16

5.

1. 21

2. 15

3. 8

4. 42

5. 25

6.

1. 20

2. 15

3. 4

4. 12

5. 9

7.

1. 70

2. 35

3. 5

4. 20

5. 25

8.

1. 126

2. 15

3. 24

4. 120

5. 720

9.

1. 24

2. 16

3. 8

4. 0

5. 1

10.

1. 6

2. 9

3. 8

4. 0

5. 1

$$10$$

1.

1. 3

2. 2

3. 1

4. 0

5. 4

2.

1. 1

2. 0

3. 2

4. 6

5. 9

3.

1. 6

2. 9

3. 1

4. 0

5. 3

4.

1. 4

2. 7

3. 12

4. 1

5. 24

5.

1. 4

2. 7

3. 12

4. 1

5. 24

6.

1. 6

2. 7

3. 8

4. 1

5. 24

7.

1. 1

2. 0

3. 16

4. 24

5. 8

8.

1. 24

2. 8

3. 16

4. 1

5. 0

9.

1. 5

2. 9

3. 20

4. 1

5. 120

10.

1. 5

2. 9

3. 20

4. 1

5. 120

$$11$$

1.

1. 21

2. 7

3. 20

4. 100

5. 30

2.

1. 35

2. 7

3. 25

4. 100

5. 30

3.

1. 21

2. 10

3. 25

4. 120

5. 0

4.

1. 2

2. 1

3. 10

4. 25

5. 0

5.

1. 35

2. 11

3. 30

4. 720

5. 1

6.

1. 7

2. 11

3. 30

4. 720

5. 1

7.

1. 7

2. 12

3. 6

4. 30

5. 4

8.

1. 1

2. 5

3. 12

4. 18

5. 3

9.

1. 2

2. 4

3. 6

4. 0

5. 1

10.

1. 1

2. 0

3. 2

4. 3

5. 7

$$12$$

1. , .

1. 9

2. 6

3. 8

4. 5

5. 3

2. , .

1. 12

2. 7

3. 9

4. 10

5. 11

3. , .

1. 16

2. 8

3. 4

4. 12

5. 20

4. , .

1. 12

2. 7

3. 9

4. 16

5. 6

5.

1. 60

2. 48

3. 120

4. 36

5. 12

6.

1. 210

2. 120

3. 150

4. 49

5. 196

7.

1. 10

2. 25

3. 125

4. 120

5. 12

8.

1. 20

2. 9

3. 12

4. 36

5. 54

9.

1. 15

2. 20

3. 48

4. 36

5. 24

10.

1. 6

2. 30

3. 120

4. 36

5. 25

$$13$$

1. Сколько слов можно получить, переставляя буквы слова «граф»?

«Граф» сөздiң әрiптерiн аустыра отырып қанша сөз алуға болады?

1. 24

2. 40

3. 256

4. 64

5. 10

2. Сколько слов можно получить, переставляя буквы слова «заказ»?

«Заказ» сөздiң әрiптерiн аустыра отырып қанша сөз алуға болады?

1. 120

2. 24

3. 30

4. 10

5. 56

3. Сколько трехзначных чисел можно написать с помощью цифр 3 и 6?

3 және 6 цифрларының көмегiмен әртүрлi қанша үш таңбалы сан жазуға болады?

1. 8

2. 9

3. 5

4. 6

5. 7

4. Сколько трехзначных чисел можно написать с помощью цифр 1, 2 и 3?

1, 2, 3 цифрларының көмегiмен әртүрлi қанша үш таңбалы сан жазуға болады?

1. 27

2. 9

3. 25

4. 16

5. 24

5. Сколько двузначных чисел можно написать с помощью цифр 2, 3 и 4?

2, 3 және 4 цифрлардың көмегiмен әртүрлi қанша екi таңбалы сан жазуға болады?

1. 9

2. 8

3. 6

4. 7

5. 10

6. Сколько двузначных чисел можно написать с помощью цифр 2, 4, 6, 8?

2, 4, 6, 8 цифрлардың көмегiмен әртүрлi қанша екi таңбалы сан жазуға болады?

1. 16

2. 24

3. 25

4. 20

5. 21

7. Сколько пятизначных чисел можно написать с помощью цифр 1, 1, 2, 3, 3?

1, 1, 2, 3, 3 цифрлардың көмегiменқанша бес таңбалы сан жазуға болады?

1. 30

2. 120

3. 24

4. 50

5. 10

8. Сколько пятизначных чисел можно написать с помощью цифр 3, 3, 3, 8, 8?

3, 3, 3, 8, 8 цифрлардың көмегiмен қанша бес таңбалы сан жазуға болады?

1. 10

2. 8

3. 9

4. 11

5. 7

9. Сколько слов можно получить, переставляя буквы слова «математика»?

«Математика» сөздiң әрiптерiн аустыра отырып қанша сөз алуға болады?

1. 151200

2. 15120

3. 10!

4. 10¹⁰

5. 1512

10. Сколько слов можно получить, переставляя буквы слова «алгоритм»?

«Алгоритм» сөздiң әрiптерiн аустыра отырып қанша сөз алуға болады?

1. 40320

2. 4032

3. 80

4. 100

5. 1000

$$14$$

1.

1. 3

2. -3

3. 0

4. 2

5. 1

2.

1. 0

2. 1

3. 2

4. -1

5. -2

3. 5 компьютер және 4 тұтынушы (қолданушы) бар. Тұтынушыларды компьютерлерге неше тәсілмен орналастыруға болады, тұтынушылардың әр қайсысына компьютер жетуі керек?

1. 120

2. 10!

3. 120

4. 140

5. 7!

4. 4 құжатты 25 орынға неше тәсілмен орналастыруға болады?

1. А⁴₂₅

2. А²⁵₄

3. С⁴₂₅

4. С⁴₅

5. А⁴₅

5. Студенттерге 8 күн ішінде 4 емтихан тапсыру керек. Осыны неше тәсілмен істеуге болады?

1. 8!/4!

2. 840

3. 1680

4. 8!

5. 64

6. С₁₀⁴ теру саны нешеге тең?

1. 210

2. 10!

3. (10-2)!

4. 21

5. 420

7. С₈³ теру саны нешеге тең?

1. 56

2. (8+3)!

3. (8-3)!

4. 24

5. 240

8. А₇³ орналастыру саны нешеге тең?

1. 210

2. 840

3. 10!

4. 4!

5. 21

9. 100 сарбаздың екеуін қарауылға шығарудың барлық мүмкіндігі қанша болады?

1. 4950

2. 2950

3. 3950

4. 1950

5. 5950

10.

1. 1

2. -1

3. -3

4. 3

5. 0

$$15$$

1.

1. -3

2. 3

3. 4

4. 0

5. 1

2.

1. -4

2. 4

3. -10

4. 10

5. 9

3.

1. -4

2. 8

3. -10

4. 7

5. 9

4.

1. -10

2. 10

3. -4

4. 4

5. 0

5.

1. 

2. 

3. 

4. 

5. 

6. Найдите образ отрезка при отображении :

кесiндiнiң бейнелеудегi бейнесiн табыңыз:

1. 

2. 

3. 

4. 

5. Нет прав.ответа/дұрыс жауабы жоқ

7. Найдите образ отрезка при отображении :

кесiндiнiң бейнелеудегi бейнесiн табыңыз:

1. 

2. 

4. 

5. Нет прав.ответа/дұрыс жауабы жоқ

8. Найдите образ отрезка при отображении :

кесiндiнiң бейнелеудегi бейнесiн табыңыз:

5. Нет прав.ответа/дұрыс жауабы жоқ

9. Найдите образ отрезка при отображении :

кесiндiнiң бейнелеудегi бейнесiн табыңыз:

1. 

2. 

4. 

10. Найдите образ отрезка при отображении :

кесiндiнiң бейнелеудегi бейнесiн табыңыз:

1. 

$$16$$

1. Найдите образ отрезка при отображении :

кесiндiнiң бейнелеудегi бейнесiн табыңыз:

1. 

2. Найдите образ отрезка при отображении :

кесiндiнiң бейнелеудегi бейнесiн табыңыз:

1. 

3. 3,4,5,7 цифрларымен жасалатын, цифр қайталанбайтын барлық үш таңбалы сандар нешеу?

1. 24

2. 54

3. 14

4. 34

5. 44

4. А және В жиындары үшін жиынының кез келген ішкі жиынын ... қатынас деп атайды.

1. бинарлық

2. эквиваленттік

3. реттік

4. унарлық

5. инверсиялық

5. А және В жиындары үшін А жиынының кез-келген элементі В жиынға да элемент болатын болса, А жиынын В жиынының ... деп атайды.

1. ішкі жиыны

2. кванторы

3. элементі

4. предикаты

5. қамтылуы

6. Егер А = {1;2;3}; В = {2;3;4;}; С = {1;2;3;4} болса,С жиынын таңдаңыз?

3. А\В

4. В\А

5. дұрыс жауабы жоқ

7. Егер А = {1;2;3}; В = {2;3;4;}; С = {2;3} болса,С жиынын таңдаңыз?

2. А\В

3. В\А

5. дұрыс жауабы жоқ

8. А = {1;2} В = {2;3}, ВхА табыңыз?

1. {(2;1);(2;2);(3;1);(3;2)}

2. {(1;2);(1;1);(2;1);(2;2)}

3. {(1;2);(1;3);(2;2);(2;3)}

4. {(2;3);(2;2);(3;2);(3;3)}

5. {(1;1);(1;2);(2;2);(3;3)}

9. А = {3;5} В = {4;6}, АхВ табыңыз?

1. {(3;4);(3;6);(5;4);(5;6)}

2. {(4;3);(4;5);(6;3);(6;5)}

3. {(3;3);(3;4);(4;3);(4;6)}

4. {(4;3);(4;4);(6;3);(6;6)}

5. {(4;5);(6;5);(6;3);(4;3)}

10. А = {1;2} В = {2;3}, АхВ табыңыз?

1. {(1;2);(1;3);(2;2);(2;3)}

2. {(2;1);(2;2);(3;1);(3;2)}

3. {(1;2);(1;1);(2;1);(2;2)}

4. {(2;3);(2;2);(3;2);(3;3)}

5. {(1;1);(1;2);(2;2);(3;3)}

$$17$$

1. Егер А = {1;2;3}; В = {2;3;4;}; С = {4} болса,С жиынын таңдаңыз?

1. В\А

3. А\В

5. дұрыс жауабы жоқ

2. Егер А = {1;2;3}; В = {2;3;4;}; С = {1} болса,С жиынын таңдаңыз?

1. А\В

3. В\А

5. дұрыс жауабы жоқ

3. 9,7,3 цифрлары әр санда бір-ақ рет қайталануға тиіс болса, осы

цифрлардан неше үш орынды сан құрауға болады?

1. 6

2. 9

3. 20

4. 15

5. 3

4. Теріс бүтін сандар жиыны мен теріс емес бүтін сандар жиынының бірігуін табу керек.

1. Натурал сандар жиыны

2. Рационал сандар жиыны

3. Нақты сандар жиыны

4. Бүтін сандар жиыны

5. Бос жиын

5. Қандай жағдайда В жиыны А-ға ішкі жиын болады?

1. А={1,2,3,4,5,6}, В={3,4,5}

2. А={a,b,c}, В={a,b,c,d,e}

3. А=Ø, В={15,16,17,18}

4. А={a,b,c,d,e}, В={c,d,e,f,g}

5. А={1,2,3,4,5}, В={І,ІІ,ІІІ}

6. А={2;4;6} және В={1;3} декарттық көбейтіндісін табу керек.

1. {(2;1),(2;3),(4;1),(4;3),(6;1),(6;3)}

2. {1,2,3,4,6}

3. {21,21,41,43,61,63}

4. {{2;1},{2;3},{4;1},{4;3},{6;1},{6;3}}

5. Ø

7. “х3= – 8” пікірінің ақиқаттық мәндерін табыңыз

1. х= – 2

2. х= 2

3. х= – 4

4. х= – 8

5. х= 4

8. А={3,4}, В={5,6} жиындардың декарттық көбейтіндісін жазыңдар.

1. {(3, 5), (3, 6), (4, 5), (4, 6)}

2. {(3, 3), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}

3. {15,16,18, 24}

4. {9, 15, 18, 16, 20, 24, 25, 36}

5. {3, 4, 5, 6}

9. R(a,b):(b/a=2/3) бинарлық қатысын қанағаттандыратын жұптарды анықтаңдар:

1. (9,6) және (21,14)

2. (12,8) және (15,9)

3. (15,10) және (6,9)

4. (14,10) және (9,6)

5. (16,8) және (9,6)

10. Ақиқат пікірді табыңыз: 1) 2<0. 2) -6>-7. 3) -2>3.

1. 2

2. 1,2

3. 2,3

4. 3

5. 1,3

$$18$$

1.

1. 8

2. 7

3. 20

4. 100

5. 30

2.

1. 28

2. 7

3. 25

4. 100

5. 30

3.

1. 56

2. 10

3. 25

4. 120

5. 0

4.

1. 56

2. 1

3. 10

4. 45

5. 0

5.

1. 70

2. 11

3. 30

4. 720

5. 1

6.

6. 56

7. 11

8. 30

9. 720

10. 1

7.

1. 8

2. 12

3. 6

4. 30

5. 4

8.

1. 336

2. 58

3. 126

4. 18

5. 3

9.

1. 9

2. 4

3. 6

4. 0

5. 1

10.

1. 72

2. 0

3. 28

4. 36

5. 7

$$19$$

1.Ақиқат немесе жалған екендігі туралы айтуға болатын байланысты баяндамалы сөйлемді қалай атаймыз?

1. тұжырым

2. жиын

3. ішкі жиын

4. предикат

5. квантор

2. a V b операциясы -

1. дизъюнкция

2. конъюнкция

3. терістеу / отрицание

4. импликация

5. эквиваленция

3. а Λ b операциясы -

1. конъюнкция

2. дизъюнкция

3. терістеу / отрицание

4. импликация

5. эквиваленция

4. ab операциясы -

1. импликация

2. терістеу / отрицание

3. дизъюнкция

4. эквиваленция

5. конъюнкция

5. a~b операциясы -

1. эквиваленция

2. импликация

3. конъюнкция

4. дизъюнкция

5. терістеу / отрицание

6. ¬a операциясы -

1. терістеу / отрицание

2. дизъюнкция

3. импликация

4. конъюнкция

5. эквиваленция

7. a Λ b формуласы мынаған тепе-тең

1. b Λ a

2. bVa

3. aVb

4. a + b

5. a * b

8. a V b формуласы мынаған тепе-тең

1. b V a

2. a * b

3. a + b

4. b Λ a

5. a - b

9. “ 2 > 8” - бұл қандай пікір?

1. жалған

2. ақиқат

3. терістеу

4. сұраулы

5. хабарлы

10. а пікірін теріске шығаратын жаңа пікір қалай белгіленеді.

1. 

2. 

3. 

4. 

5. 

$$20$$

1. - белгісі пікірде қандай мағынаны білдіреді?

1. және

2. немесе

3. ақиқат

4. жалған

5. жиын

2. - белгісі пікірде қандай мағынаны білдіреді?

1. немесе

2. және

3. ақиқат

4. жалған

5. жиын

3. (Λ) символы программада былай жазылады

1. and

2. or

3. not

4. to

5. if

4. (V) символы программада былай жазылады

1. or

2. and

3. not

4. to

5. if

5. (¬) символы программада былай жазылады

1. not

2. and

3. or

4. to

5. if

6. (and) операторына қандай логикалық символ сәйкес келедi:

1. Λ

2. V

3. ~

4. 

5. ¬

7. (or) операторына қандай логикалық символ сәйкес келедi:

1. V

2. Λ

3. ~

4. 

5. ¬

8. (not) операторына қандай логикалық символ сәйкес келедi:

1. ¬

2. Λ

3. ~

4. 

5. V

9. Ақиқат кестесімен берілген логика алгебрасының операциясын таңдаңыз:

а	b	c
1	1	1
1	0	0
0	1	1
0	0	1

1. с= ab

2. с= a V b

3. с= а Λ b

4. с= a~b

5. дұрыс жауабы жоқ

10. Ақиқат кестесімен берілген логика алгебрасының операциясын таңдаңыз:

а	b	c
1	1	1
1	0	0
0	1	0
0	0	1

1. с= a~b

2. с= ab

3. с= a V b

4. с= а Λ b

5. дұрыс жауабы жоқ

$$21$$

1. Ақиқат кестесімен берілген логика алгебрасының операциясын таңдаңыз:

а	b	c
1	1	1
1	0	1
0	1	1
0	0	0

1. с= a V b

2. с= a~b

3. с= ab

4. с= а Λ b

5. дұрыс жауабы жоқ

2. Ақиқат кестесімен берілген логика алгебрасының операциясын таңдаңыз:

а	b	c
1	1	1
1	0	0
0	1	0
0	0	0

1. с= а Λ b

2. с= a~b

3. с= ab

4. с= a V b

5. дұрыс жауабы жоқ

3. Тұжырым деп нені айтамыз?

1. ақиқаттығы немесе жалғандығы туралы айтуға болатын байланысты баяндамалы сөйлем

2. ақиқаттығы туралы айтуға болатын байланысты баяндамалы сөйлем

3. жалғандығы туралы айтуға болатын байланысты баяндамалы сөйлем

4. байланысты баяндамалы сөйлем

5. кез келген сөйлем

4. Бір ғана тұжырымнан тұратын айтылым қалай айтылады?

1. қарапайым

2. күрделі

3. ақиқат

4. жалған

5. тұжырым

5. Қарапайым тұжырым деп нені айтамыз?

1. бір ғана тұжырымнан тұратын айтылым

2. бір неше тұжырымнан тұратын айтылым

3. байланысты тұжырымдар

4. дұрыс жауабы жоқ

5. барлық жауабы дұрыс

6. Грамматикалық байланыстар көмегімен құрылған тұжырымдар қалай аталады?

1. күрделі

2. жай

3. жалған

4. қарапайым

5. ақиқат

7. Күрделі тұжырым деп нені айтамыз?

1. грамматикалық байланыстар көмегімен құрылған тұжырым

2. бір ғана тұжырымнан тұратын айтылым

3. байланысты тұжырымдар

4. дұрыс жауабы жоқ

5. барлық жауабы дұрыс

8. Қарапайым тұжырымдарды көрсетіңіз:

1_ 8 март - Әйелдер мейрамы

2_ Егер сан 6 ға бөлінсе, ол 4 ке бөлінеді

3_ Егер бүгін сенбі болса, ертең жексенбі болады

4_ Кез келген сан 3 ке бөлінеді

1. 1,4

2. 1,2

3. 1,3

4. 2,3

5. 2,4

9. Күрделі тұжырымдарды көрсетіңіз:

1_ 8 март - Әйелдер мейрамы

2_ Егер сан 6 ға бөлінсе, ол 4 ке бөлінеді

3_ Егер бұгін сенбі болса, ертең жексенбі болады

4_ Кез келген сан 3 ке бөлінеді

1. 2,3

2. 2,4

3. 1,2

4. 1,4

5. 1,3

10. Тұжырымдар мәні бойынша қандай екі класқа бөлінеді?

1. ақиқат және жалған

2. қарапайым және күрделі

3. қарапайым және қарапайым емес

4. күрделі және күрделі емес

5. ақиқат және ақиқат

$$22$$

1. Егер а ақиқат болса, онда

1. а=1

2. а=0

3. а=2

4. а=-1

5. а=А

2. Ақиқат тұжырымды көрсетіңіз:

1. 6 – жұп сан

2. 5 – жұп сан

3. егер сан 5 бөлінсе, онда ол 0 ге бөлінеді

4. 0 >5

5. дұрыс жауабы жоқ

3. Тұжырымдарға қолданылатын логикалық амалды көрсетіңіз:

1. терістеу

2. көбейту

3. Салыстыру

4. Бөлу

5. қосу

4. Терістеу амалының анықтамасын көрсетіңіз:

1. а ақиқат болғанда а емес – жалған

2. а ақиқат болғанда, а емес – ақиқат

3. а ақиқат болғанда, а – жалған

4. а ақиқат болғанда, а - жалған және ақиқат

5. а жалған болғанда, а емес – жалған

5. Ақиқаттық кесте деп нені айтамыз:

1. тұжырымның мұмкін болған барлық логикалық мәндері

2. тұжырымның екі мәнінен тұратын кесте

3. барлық мәндері ақиқат кесте

4. қарапайым тұжырымдардан тұратын кесте

5. күрделі тұжырымдардан тұратын кесте

6. «4 кіші 10 нан» тұжырымына терістеу амалын қолдаңыз:

1. 4 кіші емес 10 нан

2. 4 кіші 10 нан

3. 4 үлкен емес 10 нан

4. 4 тең 10 ға

5. 4 кіші не тең 10 ға

7. Тұжырымдардың конъюнкциясы деп неге айтылады?

1. тек екі тұжырым да ақиқат болғанда ақиқат тұжырым

2. тек екі тұжырым да ақиқат болғанда жалған тұжырым

3. екі тұжырым да жалған болғанда жалған тұжырым

4. екі тұжырым да жалған болғанда ақиқат тұжырым

5. тұжырымдардың бірі ақиқат, екіншісі жалған болғанда ақиқат тұжырым

8. Екі тұжырым берілген: 1) «6 2 ге бөлінеді»; 2) «6 3 ке бөлінеді». Конъюнкция амалын қолдаңыз:

1. «6 2 ге бөлінеді және 6 3 ке бөлінеді»

2. «6 2 ге немесе 3 ке бөлінеді»

3. «6 2 ге бөлінеді»

4. «6 3 ке бөлінеді»

5. «6 2 ге бөлінеді және 3 ке бөлінбейді»

9. Тұжырымдардың дизъюнкциясы деп неге айтылады?

1. тек екі тұжырымда жалған болғанда жалған тұжырым

2. тек екі тұжырымда жалған болғанда ақиқат тұжырым

3. тек екі тұжырымда ақиқат болғанда ақиқат тұжырым

4. тек екі тұжырымда ақиқат болғанда жалған тұжырым

5. бірі ақиқат және бірі жалған болғанда ақиқат тұжырым

10. Екі тұжырым берілген: 1) «Ертең қар жауады»; 2) «Қар жаумайды». Дизъюнкция амалын қолдаңыз:

1. «Ертең қар жауады немесе қар жаумайды»

2. «Ертең қар жауады және қар жаумайды»

3. «Ертең қар жауады»

4. «Ертең қар жаумайды»

5. «Ертең жаңбыр жауады»

$$23$$

1. Эквиваленция амалының анықтамасын көрсетіңіз:

1. тұжырымдар бірдей мән қабылдаса – ақиқат тұжырым

2. тұжырымдар бірдей мән қабылдаса - жалған тұжырым

3. екі тұжырымда ақиқат болса – жалған тұжырым

4. екі тұжырымда жалған болса – жалған тұжырым

5. бірі ақиқат, екіншісі жалған болса – ақиқат тұжырым

2. Импликация амалының анықтамасын көрсетіңіз:

1. егер а ақиқат, b жалған болса - жалған тұжырым

2. егер а ақиқат, b жалған болса - ақиқат тұжырым

3. егер а жалған, b ақиқат болса - жалған тұжырым

4. егер а жалған, b ақиқат болса - ақиқат тұжырым

5. бірі ақиқат, екіншісі жалған болса – жалған тұжырым

3. → символының логикалық мәні:

1. импликация

2. конъюнкция

3. Дизъюнкция

4. Эквиваленция

5. терістеу

4. ~ символының логикалық мәні:

1. эквиваленция

2. конъюнкция

3. дизъюнкция

4. импликация

5. терістеу

5. Λ символының логикалық мәні:

1. конъюнкция

2. эквиваленция

3. дизъюнкция

4. импликация

5. терістеу

6. V символының логикалық мәні:

1. дизъюнкция

2. конъюнкция

3. эквиваленция

4. импликация

5. терістеу

7. ¬ символының логикалық мәні:

1. терістеу

2. конъюнкция

3. эквиваленция

4. импликация

5. дизъюнкция

8. Егер x=1, y=1, z=0 болса, ¬(хΛу)V¬z формуласының логикалық мәнін табыңыз:

1. 1

2. 0

3. -1

4. 0,5

5. 0 және 1

9. Егер x=1, y=1, z=1 болса, ¬(хΛу)V¬z формуласының логикалық мәнін табыңыз:

1. 0

2. 1

3. -1

4. 0,5

5. 0 және 1

10. Егер формуланың құрамына 3 тұжырым енетін болса, онда ақиқаттық кесте неше қатардан тұрады?

1. 8

2. 9

3. 3

4. 6

5. 1

$$24$$

1. Егер формуланың құрамына 2 тұжырым енетін болса, онда ақиқаттық кесте неше қатардан тұрады?

1. 4

2. 3

3. 8

4. 2

5. 1

2. Егер формуланың құрамына 4 тұжырым енетін болса, онда ақиқаттық кесте неше қатардан тұрады?

1. 16

2. 8

3. 9

4. 2

5. 1

3. Пара-пар формулалар деп неге айтылады?

1. егер екі формула бірдей нәтижелі қабылдаса

2. егер екі формула әр тұрлі нәтиже қабылдаса

3. егер екі формула бірдей мән қабылдаса

4. егер екі формула әр тұрлі мән қабылдаса

5. егер формуланың мәні 0 ге тең болса

4. Формулалардың пара-парлығы қандай символмен белгіленеді?

1. А≡В

2. А↔В

3. А=В

4. А+В

5. А–В

5. Қандай формула тепе-тең ақиқат деп айтылады?

1. егер формула өзінің барлық мәндерінде 1 мәнді қабылдаса

2. егер формула өзінің барлық мәндерінде 0 мәнді қабылдаса

3. егер формула тек 0 және 1 мәндерін қабылдаса

4. егер формула пара-пар болса

5. егер формула ақиқат болса

6. Қандай формула тепе-тең жалған деп айтылады?

1. егер формула өзінің барлық мәндерінде 0 мәнді қабылдаса

2. егер формула өзінің барлық мәндерінде 1 мәнді қабылдаса

3. егер формула тек 0 және 1 мәндерін қабылдаса

4. егер формула пара-пар болса

5. егер формула ақиқат болса

7. Пара-пар формулаларды көрсетiңiз:

1. 

2. 

3. 

4. 

5. 

8. Пара-пар формулаларды көрсетiңiз:

1. ,

2. ,

3. ,

4. ,

5. ,

9. Пара-пар формулаларды көрсетiңiз:

1. ,

2. ,

3. ,

4. ,

5. ,

10. Пара-пар формулаларды көрсетiңiз:

1. ,

2. ,

3. ,

4. ,

5. ,

$$25$$

1. Пара-пар формулаларды көрсетiңiз:

1. ,

2. ,

3. ,

4. ,

5. ,

2. Қарапайым конъюнкция деп неге айтылады?

1. тұжырымдардың немесе олардың терістеулерінің конъюнкциясы

2. тұжырымдардың немесе олардың терістеулерінің дизъюнкциясы

3. тұжырымдардың конъюнкциясы немесе дизъюнкциясы

4. тұжырым терістеулерінің конъюнкциясы және дизъюнкциясы

5. тұжырымдырдың конъюнкциясы және дизъюнкциясы

3. Қарапайым дизъюнкция деп неге айтылады?

1. тұжырымдардың немесе олардың терістеулерінің дизъюнкциясы

2. тұжырымдардың немесе олардың терістеулерінің конъюнкциясы

3. тұжырымдардың конъюнкциясы немесе дизъюнкциясы

4. тұжырым терістеулерінің конъюнкциясы және дизъюнкциясы

5. тұжырымдырдың конъюнкциясы және дизъюнкциясы

4. Конъюнктивті нормал форма (КНФ) дегеніміз не?

1. қарапайым дизъюнкциялардың конъюнкция көмегімен байланысы

2. қарапайым конъюнкциялардың дизъюнкция көмегімен байланысы

3. тұжырым конъюнкциялардың терістеуі

4. тұжырым конъюнкциялары және дизъюнкциялары

5. тұжырым конъюнкциясы немесе дизъюнкциясы

5. Дизъюнктивті нормал форма (ДНФ) дегеніміз не?

1. қарапайым конъюнкциялардың дизъюнкция көмегімен байланысы

2. қарапайым дизъюнкциялардың конъюнкция көмегімен байланысы

3. тұжырым конъюнкциялардың терістеуі

4. тұжырым конъюнкциялары және дизъюнкциялары

5. тұжырым конъюнкциясы немесе дизъюнкциясы

6. Жетілдірілген дизъюнктивті нормал форма (ЖДНФ) дегеніміз не?

1. әрбір тұжырымның ДНФ да міндетті түрде болуы

2. әрбір тұжырымның КНФ да міндетті түрде болуы

3. тұжырым конъюнкциялардың терістеуі

4. тұжырым конъюнкциялары және дизъюнкциялары

5. тұжырым конъюнкциясы немесе дизъюнкциясы

7. Жетілдірілген конъюнктивті нормал форма (ЖКНФ) дегеніміз не?

1. әрбір тұжырымның КНФ да міндетті түрде болуы

2. әрбір тұжырымның ДНФ да міндетті түрде болуы

3. тұжырым конъюнкциялардың терістеуі

4. тұжырым конъюнкциялары және дизъюнкциялары

5. тұжырым конъюнкциясы немесе дизъюнкциясы

8. Дизъюнкция үшiн де Морган заңы келесi түрде жазылады:

1. 

9. Конъюнкция үшiн де Морган заңы келесi түрде жазылады:

1. 

5. 

10. Дизъюнкция үшiн коммутативтiк заңын көрсетiңiз:

1. 

2. 

3. 

4. 

5. 

$$26$$

1. Бинар предикат дегеніміз не?

1. Р (a₁, a₂,…,a_n) – n – арный предикат при n=2

2. Р (a₁, a₂,…,a_n) – n – арный предикат при n=3.

3. Р (a₁, a₂,…,a_n) – n – арный предикат при n=1

4. Р (a₁, a₂,…,a_n) – n – арный предикат при n=0

5. Р (a₁, a₂,…,a_n) – n – арный предикат при n= -1

2. «Бүгін дүйсенбі немесе сейсенбі» деген пікірді логикалық формуламен көрсетіңіз.

1. 

2. 

3. 

4. 

5. 

3. «Қар немесе жауын жауып тұр» деген пікірді логикалық формуламен көрсетіңіз.

2. B)

3. C)

4. D)

5. E)

4. «Егер жауын жауса, онда төбе су болады. Жауын жоқ , ал төбе су» деген пікірді логикалық формуламен көрсетіңіз.

1. 

2. 

3. 

4. 

5. 

5. Предикат дегеніміз не?

1. айнымалысыз сөйлемдер

2. тавтология немесе логиканың заңы

3. айнымалылы сөйлемдер

4. қайшылық немесе жалғанға тепе-тең формула

5. қарапайым пікір

6. Құрамында айнымалылардың орнына белгілі бір объектілерді қоюға болатын айнымалылы сөйлемін қандай орынды предикат деп айтады?

1. n-орынды

2. бір орынды

3. екі орынды

4. үш орынды

5. төрт орынды

7. х + у= 3 предикаты неше орынды?

1. екі орынды

2. бір орынды

3. n-орынды

4. үш орынды

5. төрт орынды

8. Квантордың барлық түрлерін көрсет?

1. жалпылау және бар болу немесе табылу

2. жалпылау

3. бар болу немесе табылу

4. бар болу

5. дұрыс жауап жоқ

9. Екі рет теріске шығару заңын көрсет.

1. 

2. 

3. 

4. 

5. 

10. =0 теңдеуін шешіңіз.

1. x=0,y=0

2. x=1,y=0

3. x=0,y=1

4. x=1,y=1

5. x=y

$$27$$

1. xy=1 теңдеуін шешіңіз

1. x=1,y=1

2. x=1,y=0

3. x=0,y=1

4. x=0,y=0

5. x=y

2. теңдеуін шешіңіз

1. x=0,y=1

2. x=1,y=0

3. x=1,y=1

4. x=0,y=0

5. x=y

3. теңдеуін шешіңіз.

1. x=0,y=0

2. x=0,y=1

3. x=1,y=1

4. x=1,y=0

5. шешімі жоқ

4. теңдеуін шешіңіз.

1. шешімі жоқ

2. x=1,y=0

3. x=0,y=1

4. x=1,y=1

5. x=0,y=0

5. теңдеуін шешіңіз.

1. x=1,y=1

2. x=1,y=0

3. x=0,y=1

4. x=0,y=0

5. шешімі жоқ

6. Унар предикат дегеніміз не?

1. Р (a₁, a₂,…,a_n) – n – арный предикат при n=3.

2. Р (a₁, a₂,…,a_n) – n – арный предикат при n=2

3. Р (a₁, a₂,…,a_n) – n – арный предикат при n=0

4. Р (a₁, a₂,…,a_n) – n – арный предикат при n=1

5. Р (a₁, a₂,…,a_n) – n – арный предикат при n=-1

7. Жай сөйлемдерді логикалық жалғаулармен байланыстырып қандай сөйлемдер алуға болады?

1. құрама сөйлемдер

2. айтылымдар

3. предикаттар

4. теңбе-тең формулалар

5. тавтология

8. Берiлген сөйлем кванторлар арқылы қалай жазылады ? «х+10=х болатындай х саны табылмайды».

1. x (x 10 x)

2. x (x 0 x)

3. xy z (x y z)

4. x z (x 10 2)

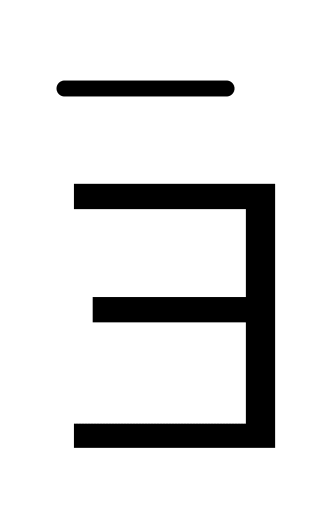5. x (x 10 2) .

9. Берiлген сөйлем кванторлар арқылы қалай жазылады ? «x+10=2 болатындай x саны табылады».

1. x (x 10 2)

2. x (x 0 x)

3. xy z (x y z)

4. x z (x 10 2)

5. x (x 10 x).

10. Топтағы 10 студенттен ЭЕМ-де жұмыс істеу үшін 2 адамды таңдау керек.

Мұны неше тәсілмен орындауға болады?

1. 45

2. 90

3. 20

4. 15

5. 10

$$28$$

1.10 цифрдан төрт орынды әр түрлі қанша автомашина нөмірін құрастыруға юолады?

1. 10⁴

2. 40

3. 10!

4. 45

5. 24

2. Төмендегi айтылымды теңбе-тең болатындай дизьюнкциямен алмастырыңыз х²-5х+6=0

1. (х-3=0)V(х-2=0)

2. (х-3=0)^(х-2=0)

3. (х-3≠0)V(х-2=0)

4. (х-3≠0)V(х-2≠0)

5. (х-3=0)^( х-2≠0)

3. Коньюнкция схемасы қандай?

1. және

2. немесе

3. жоқ

4. иә

5. дұрыс жауабы жоқ

4. Дизьюнкция схемасы қандай?

1. немесе

2. және

3. жоқ

4. иә

5. дұрыс жауабы жоқ

5. Терістеудің схемасы қандай?

1. жоқ

2. немесе

3. және

4. иә

5. дұрыс жауабы жоқ

6.Келесі теңдіктердің қасысы дұрыс:

1. A A A

2. А~В (┐A В) (А ┐B)

3. А В А ┐B

4. А В ┐А ┐B

5. А~В (A В) (А ┐B)

7. және - белгілері пікірде қандай мағананы білдіреді?

1. «егер а болса, онда b болады»

2. және

3. немесе

4. «а болғанда және тек сонда ғана b болады»

5. жиын

8. және - белгілері пікірде қандай мағананы білдіреді?

1. «а болғанда және тек сонда ғана b болады»

2. және

3. немесе

4. «егер а болса, онда b болады»

5. Жиын

9. де Морганның екінші заңы:

1. ┐(A В) ┐А ┐B

2. A A A

3. A A A

4. (A В) А B

5. ┐(A В) ┐А ┐B

10. Импликация белгісі:

2. ~

5. ┐

$$29$$

1. Эквиваленция белгісі:

1. ~

5. ┐

2. өрнегі неге тең ?

1. 1

3. 0

4. 

5. 0

6. өрнегі неге тең ?

1. 0

2. 0

3. x

4. 1

5. 1

7. өрнегі неге тең ?

1. x 1

2. 0

3. Х

4. 1

5. 0

8. өрнегі неге тең ?

1. 0

2. x

3. 1

4. 1

5. 0

9. 1 тұжырымдамасы неге тең?

1. х

2. 1

3. 0

4. 

5. x x

10. 0 өрнегі неге тең?

1. 0

2. 1

3. x

4. 0

5. x x

$$30$$

1. өрнегі неге тең ?

1. 1

2. x

3. 0

4. 1

5. 0

2.

1. 

3. 

4. 

5. 0

3.

1. 

4.

1. 

2. 

3. 

4. 

5. 0

5.

1. 

2. 

3. 

4. 

5. 0

6. Логика алгебрасының барлық n айнымалы функциялардың саны нешеге тең?

1. 2ⁿ

2. 

3. 2

4. п

5. 1

7. «5 кіші 10 нан» тұжырымына терістеу амалын қолдаңыз:

1. 5 кіші емес 10 нан

2. 5 үлкен 10 нан

3. 5 үлкен емес 10 нан

4. 5 тең 10 ға

5. 5 кіші не тең 10 ға

8. Егер x=0, y=1, z=0 болса, ¬(хΛу)V¬z формуласының логикалық мәнін табыңыз:

1. 1

2. 0

3. -1

4. 0,5

5. 0 және 1

9. Егер x=0, y=1, z=1 болса, ¬(хΛу)V¬z формуласының логикалық мәнін табыңыз:

1. 1

2. 0

3. -1

4. 0,5

5. 0 және 1

10. Егер x=0, y=0, z=1 болса, ¬(хΛу)V¬z формуласының логикалық мәнін табыңыз:

1. 1

2. 0

3. -1

4. 0,5

5. 0 және 1

$$31$$

1. Сколько петель у графа, заданного следующей матрицей смежности?

сыбайластық матрицасымен берiлген графтың қанша iлмегi бар?

1. 3

2. 0

3. 1

4. 2

5. 4

2. Сколько петель у графа, заданного следующей матрицей смежности?

сыбайластық матрицасымен берiлген графтың қанша iлмегi бар?

1. 4

2. 0

3. 1

4. 2

5. 3

3. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 5

2. 3

3. 1

4. 2

5. 4

4. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 2

2. 0

3. 1

4. 3

5. 4

5. Дана матрица смежности графа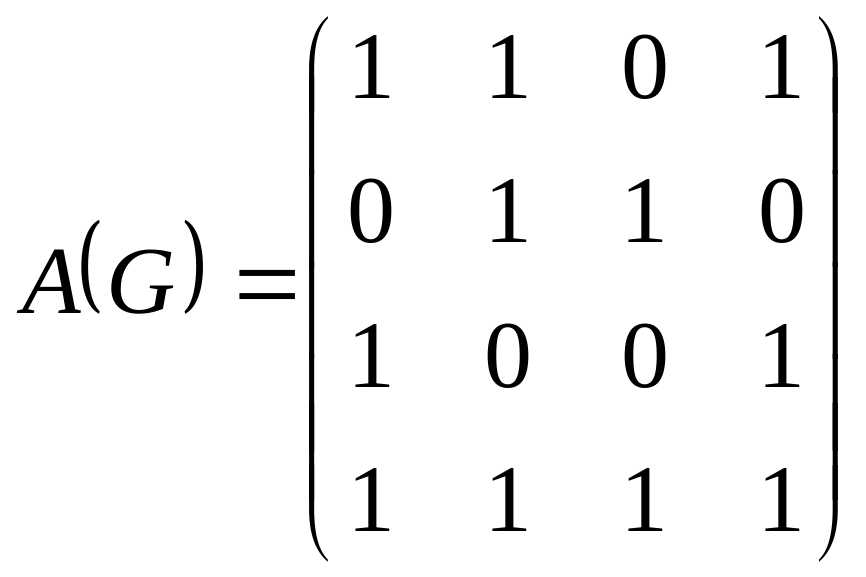

графтың сыбайластық матрицасы берiлген.

1. 3

2. 0

3. 1

4. 2

5. 4

6. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 3

2. 0

3. 1

4. 2

5. 4

7. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 6

2. 0

3. 5

4. 4

5. 3

8. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 3

2. 0

3. 1

4. 2

5. 4

9. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 2

2. 0

3. 1

4. 3

5. 4

10. Сколько петель у графа, заданного следующей матрицей смежности?

сыбайластық матрицасымен берiлген графтың қанша iлмегi бар?

1. 2

2. 0

3. 1

4. 3

5. 4

$$32$$

1. Сколько петель у графа, заданного следующей матрицей смежности?

сыбайластық матрицасымен берiлген графтың қанша iлмегi бар?

1. 1

2. 0

3. 3

4. 2

5. 4

2. Сколько петель у графа, заданного следующей матрицей смежности?

сыбайластық матрицасымен берiлген графтың қанша iлмегi бар?

1. 0

2. 3

3. 1

4. 2

5. 4

3. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 2

2. 0

3. 1

4. 3

5. 4

4. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 4

2. 0

3. 1

4. 2

5. 3

5. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 3

2. 0

3. 1

4. 2

5. 4

6. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 4

2. 0

3. 1

4. 2

5. 3

7. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 7

2. 6

3. 5

4. 3

5. 4

8. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 2

2. 3

3. 1

4. 5

5. 4

9. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 3

2. 2

3. 1

4. 5

5. 4

10. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 5

2. 3

3. 1

4. 2

5. 4

$$33$$

1. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 2

2. 3

3. 1

4. 5

5. 4

2. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 3

2. 2

3. 1

4. 5

5. 4

3. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 5

2. 3

3. 1

4. 2

5. 4

4. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 2

2. 3

3. 1

4. 5

5. 4

5. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 2

2. 3

3. 1

4. 5

5. 4

6. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 4

2. 3

3. 1

4. 5

5. 2

7. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 4

2. 3

3. 1

4. 5

5. 2

8. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 4

2. 3

3. 1

4. 5

5. 2

9. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 8

2. 6

3. 7

4. 5

5. 4

10. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 4

2. 3

3. 1

4. 5

5. 2

$$34$$

1. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 2

2. 3

3. 1

4. 5

5. 4

2. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 6

2. 7

3. 8

4. 5

5. 4

3. Дана матрица инцидентности графа

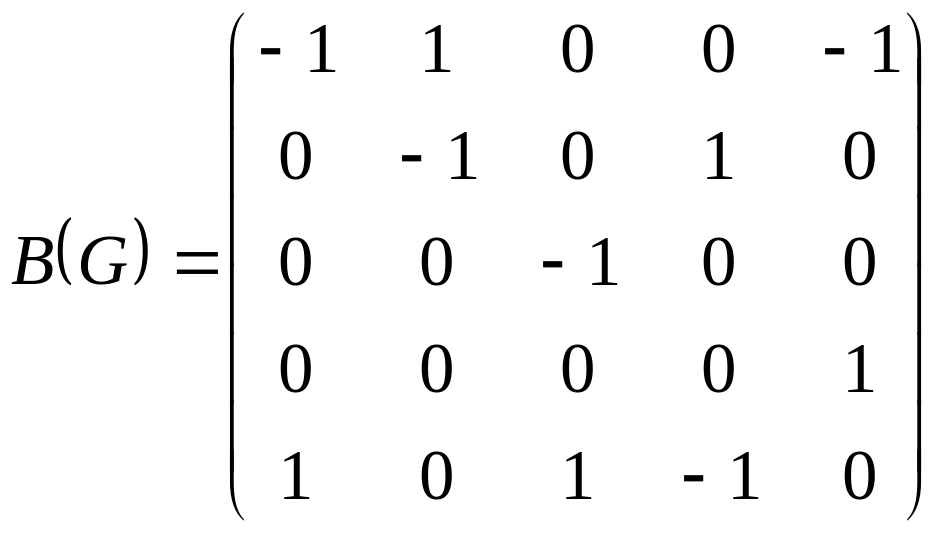
графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 1

4. 0

5. 4

4. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 2

4. 0

5. 4

5. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 2

4. 0

5. 4

6. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 2

4. 0

5. 4

7. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 1

4. 0

5. 4

8. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 1

4. 2

5. 4

9. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 2

4. 0

5. 4

10. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 1

4. 0

5. 4

$$35$$

1. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 0

4. 2

5. 4

2. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 0

2. 3

3. 2

4. 1

5. 4

3. Дана матрица инцидентности графа. Найдите цикломатическое число графа.

графтың түйiстiлiк матрицасы берiлген. Графтың цикломатикалық санын табыңыз.

1. 2

2. 3

3. 1

4. 0

5. 4

4. Дана матрица инцидентности графа. Сколько существует линейно независимых циклов графа?

графтың түйiстiлiк матрицасы берiлген. Графтың қанша сызықтық тәуелсiз циклдары бар?

1. 2

2. 3

3. 1

4. 0

5. 4

5. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 1

2. 0

3. 3

4. 2

5. 4

6. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 3

2. 0

3. 1

4. 2

5. 4

7. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 1

2. 0

3. 3

4. 2

5. 4

8. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 1

4. 0

5. 4

9. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 1

2. 0

3. 3

4. 2

5. 4

10. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 1

2. 0

3. 3

4. 2

5. 4

$$36$$

1.Дана матрица смежности графа

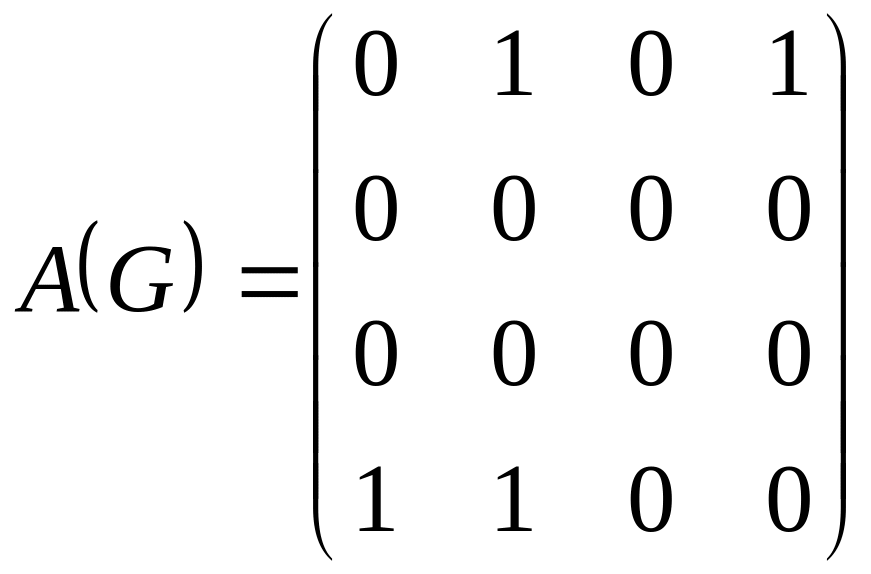
графтың сыбайластық матрицасы берiлген.

1. 2

2. 0

3. 1

4. 3

5. 4

2. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 5

2. 3

3. 1

4. 2

5. 4

3. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 5

2. 3

3. 1

4. 2

5. 4

4. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 7

2. 3

3. 6

4. 5

5. 4

5. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 6

2. 3

3. 5

4. 2

5. 4

6. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 6

2. 3

3. 5

4. 2

5. 4

7. Сколько дуг у полного графа К₅?

К₅ толық графтың қанша доғалары бар?

1. 10

2. 5

3. 9

4. 8

5. 6

8. Сколько дуг у полного графа К₆?

К₆ толық графтың қанша доғалары бар?

1. 15

2. 6

3. 9

4. 10

5. 12

9. Сколько дуг у полного графа К₇?

К₇ толық графтың қанша доғалары бар?

1. 21

2. 7

3. 14

4. 20

5. 15

10. Сколько дуг у полного графа К₈?

К₈ толық графтың қанша доғалары бар?

1. 28

2. 8

3. 16

4. 27

5. 17

$$37$$

1. Найдите общее решение рекуррентного соотношения

рекурренттiк арақатынастың жалпы шешiмiн табыңыз.

1. 

2. 

3. 

4. 

5. 

2. Найдите общее решение рекуррентного соотношения

рекурренттiк арақатынастың жалпы шешiмiн табыңыз.

1. 

2. 

4. 

5. 

3. Найдите общее решение рекуррентного соотношения

рекурренттiк арақатынастың жалпы шешiмiн табыңыз.

4. Найдите общее решение рекуррентного соотношения

рекурренттiк арақатынастың жалпы шешiмiн табыңыз.

2. 

3. 

4. 

5. Найдите общее решение рекуррентного соотношения

рекурренттiк арақатынастың жалпы шешiмiн табыңыз.

6. Найдите общее решение рекуррентного соотношения

рекурренттiк арақатынастың жалпы шешiмiн табыңыз.

7. Сколько дуг у полного графа К₄?

К₄ толық графтың қанша доғалары бар?

1. 6

2. 5

3. 8

4. 4

5. 7

8. Сколько дуг у полного графа К₉?

К₉ толық графтың қанша доғалары бар?

1. 36

2. 9

3. 18

4. 19

5. 33

9. Сколько дуг у полного графа К₁₀?

К₁₀ толық графтың қанша доғалары бар?

1. 45

2. 54

3. 10

4. 21

5. 25

10. Сколько дуг у полного графа К₁₂?

К₁₂ толық графтың қанша доғалары бар?

1. 66

2. 12

3. 25

4. 60

5. 36

$$38$$

1. Из города А в город В ведет 2 дороги, а из города В в город С – 3 дороги; имеется также 2 дороги из А в С, не проходящих через В. Сколькими способами можно добраться из А в С ?

А қаласынан В қаласына 2 жолмен, ал В қаласынан С қаласына 3 жолмен баруµа болады. А қаласынан С қаласына В дан өтпейтiн 2 жол бар. А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 8

2. 7

3. 6

4. 9

5. 10

2. Что такое конечный граф?

Ақырлы граф дегеніміз не?

1. если число его вершин конечны.

егер графтың төбелері ақырлы болса.

2. если число ребер графа конечно.

егер графтың қабырғалары ақырлы болса.

3. если число его вершин счетно.

егер графтың төбелері саналымды болса.

4. если число вершин и число ребер конечно.

егер графтың төбелері және қабырғалары ақырлы болса.

5. если число изолированных вершин конечно

егер графтың ажыратылған төбелері шекті болса

3. Что такое дерево?

Ағаш дегеніміз не?

1. конечный, связной, неориентированный граф, состоящий по крайней мере из двух вершин и не содержающий циклов.

ақырлы, байланысты, бағытталмаған, кемінде екі төбесі бар және циклге ие болмаған граф.

2. конечный, связной, неориентированный граф.

ақырлы, байланысты, бағытталмаған граф.

3. конечный, неориентированный, имеющий по крайней мере две вершины граф

ақырлы, байланысты, бағытталмаған, кемінде екі төбесі бар граф.

4. конечный, связной, состоящий по крайней мере из двух вершин граф

ақырлы, байланысты, кемінде екі төбесі бар граф.

5. конечный граф, содержащий по крайней мере две вершины.

кемінде екі төбесі бар, ақырлы граф.

4. Из города А в город В ведет 2 дороги, а из города В в город С – 3 дороги. Сколькими способами можно добраться из А в С через В?

А қаласынан В қаласына 2 жолмен, ал В қаласынан С қаласына 3 жолмен баруға болады. В қаласы арқылы А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 6

2. 5

3. 4

4. 7

5. 3

5. Из города А в город В ведет 3 дороги, а из города В в город С – 5 дорог. Сколькими способами можно добраться из А в С через В?

А қаласынан В қаласына 3 жолмен, ал В қаласынан С қаласына 5 жолмен баруға болады. В қаласы арқылы А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 15

2. 12

3. 10

4. 8

5. 14

6. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 3

2. 0

3. 1

4. 2

5. 4

7. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 1

2. 0

3. 3

4. 2

5. 4

8.Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 1

2. 0

3. 3

4. 2

5. 4

9. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 3

2. 0

3. 1

4. 2

5. 4

10. Дана матрица инцидентности графа

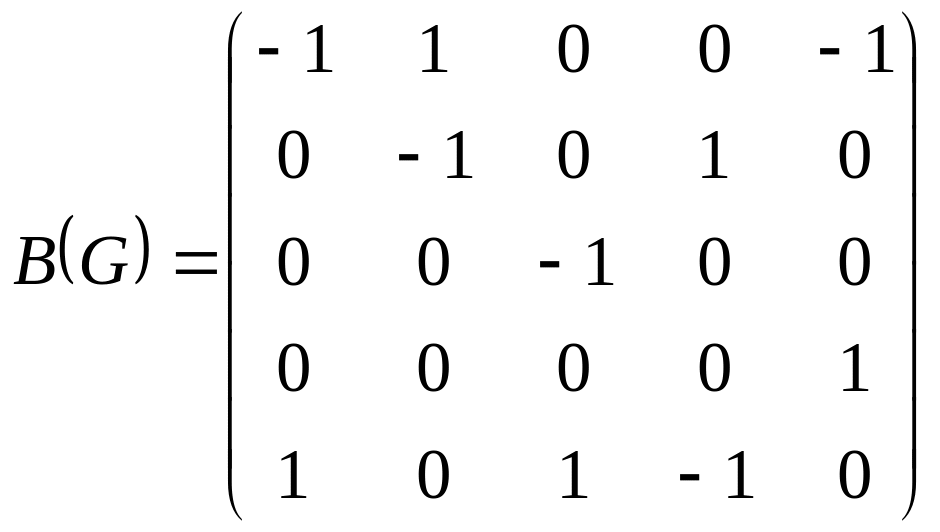
графтың түйiстiлiк матрицасы берiлген.

1. 0

2. 3

3. 1

4. 2

5. 4

$$39$$

1. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 0

2. 3

3. 1

4. 2

5. 4

2. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 0

2. 3

3. 1

4. 2

5. 4

3. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 1

4. 0

5. 4

4. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 1

4. 0

5. 4

5. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 0

4. 1

5. 4

6. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 6

2. 3

3. 5

4. 2

5. 4

7. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 3

2. 1

3. 0

4. 2

5. 4

8. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 4

2. 3

3. 5

4. 2

5. 6

9. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 5

4. 4

5. 6

10. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 2

4. 0

5. 4

$$40$$

1.Из города А в город В ведет 2 дороги, а из города В в город С 4 – дороги. Сколькими способами можно добраться из А в С через В?

А қаласынан В қаласына 2 жолмен, ал В қаласынан С қаласына 4 жолмен баруға болады. В қаласы арқылы А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 8

2. 15

3. 10

4. 6

5. 14

2. Из города А в город В ведет 3 дороги, а из города В в город С – 5 дорог; имеется также 4 дороги из А в С, не проходящих через В. Сколькими способами можно добраться из А в С ?

А қаласынан В қаласына 3 жолмен, ал В қаласынан С қаласына 5 жолмен баруға болады. А қаласынан С қаласына В дан өтпейтiн 4 жол бар. А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 19

2. 17

3. 18

4. 16

5. 15

3.Қайталанатын қабырғалары жоқ жол не деп аталады?

1. тізбе

2. орман

3. ағаш

4. граф

5. жол

4. Тұйық жолды не деп атайды?

1. цикл

2. орман

3. тізбе

4. граф

5. жол

5. Жай тізбе дегеніміз не?

1. қайталанатын төбесі жоқ тізбе

2. қайталанатын қабырғалары жоқ жол

3. бастапқы және соңғы төбесі беттесетін цикл

4. қабырғалары қайталанбайтын цикл

5. байланыссыз граф

6. Эйлер циклі деп нені айтамыз?

1. қабырғалары қайталанбайтын цикл

2. қайталанатын төбесі жоқ тізбе

3. қайталанатын қабырғалары жоқ жол

4. бастапқы және соңғы тӛбесі беттесетін цикл

5. байланыссыз граф

7. G - Эйлерлік граф болуы үшін қандай шарт орындалуы қажет?

1. байланысқан граф болу керек

2. байланыссыз граф болу керек

3. ішкі графтары болу керек

4. қабырғалары қайталанып келуі керек

5. төбелері қайталанбау керек

8. 3 орынды предикатты анықтаңыз:

1. y/x+z+sinx<0

2. x>1

3. x>y

4. xy=10

5. xy-1<0

9. Бір орынды предикатты анықтаңыз:

1. x>1

2. y/x+z+sinx<0

3. x>y

4. xy=10

5. xy-1<0

10. Толық бағытталмаған граф деген не?

1. қабырғалары (х_i,….. ) жұптар

2. қабырғалары бағытталмаған граф

3. төбелері бағытталмаған граф

4. төбелері бағытталған граф

5. қабырғалары реттелген граф

$$41$$

1. Ноль-граф деген не?

1. барлық төбелері жоқ граф

2. төбелері және қабырғалары жоқ граф

3. барлық қабырғалары жоқ граф

4. төбелері шекті болған граф

5. төбелері бар граф

2. Толық бағытталған граф деген не?

1. кез келген екі төбесі кемінде бір бағыт бойынша қосылған

2. кез келген екі қабырғасы бағытталған

3. кез келген екі төбесі бағытталған

4. кез келген екі төбесі кезкелген екі қабырғасы реттелген.

5. кез келген екі төбесі екі жағына бағытталған.

3.Байланысты граф дегеніміз не?

1. бағытталмаған және кезкелген екі төбесі байланысты граф

2. бағытталмаған және кезкелген екі төбесі байланыссыз

3. бағытталған граф

4. бағытталған және екі төбесін қосуға болады

5. бағытталған және бағытталмаған граф.

4. Графтың доғасы не?

1. бағытталған қабырға

2. қабырғасы

3. бағытталмаған қабырға

4. вектор

5. қисық

5. Аралас граф деген не?

1. бағытталған және бағытталмаған қабырғаға ие болған граф

2. ағытталған қабырғағалы граф

3. бағытталмаған қабырғағалы граф

4. төбелері және қабырғалары бағытталған

5. төбелері және қабырғалары бағытталмаған

6. Мультиграф дегені не?

1. кез келген екі төбесі бірнеше қабырғамен қосылған

2. кез келген екі төбесі шексіз көп қабырғамен қосылған

3. кез келген екі төбесі екі қабырғамен қосылған

4. бірнеше граф

5. шексіз граф

7. Графтың контуры не?

1. алғашқы төбесі соңғы төбесімен беттескен шекті жол

2. g₁,g_2,… g_n доғалар тізбегі

3. алғашқы төбесі соңғы төбесімен беттескен шексіз жол

4. графтың бірнеше қабырғалары

5. графтың барлық қабырғалары

8. Бағытталған графтың жолы не?

1. g₁,g₂…,g_n доғалар тізбегі болып, әрбір алғашқы доғаның ақыры кейінгі доғаның басы болады

2. g₁,g₂…,g_n доғалар тізбегі

3. g₁,g₂…,g_n доғалар ұзындығының қосындысы

4. графтың бірнеше қабырғасын ұзындықтары қосындысы

5. графтың барлық қабырғалары ұзындықтары қосындысы.

9. Графтың байланысты төбелері не?

1. егер төбелері х_i және x_j болатын S шынжыр бар болса

2. егер төбелері х_i және x_j болатын S контур бар болса

3. егер төбелері х_i және x_j болатын S жол бар болса

4. егер х_i және x_j болатын төбелерді қосуға болса.

5. егер х_i және x_j болатын төбелерді қосуға болмаса.

10. Бағытталмаған графтың шынжыры не?

1. қабырғалардан түзілген шекті немесе шексіз S={…, g₁,g₂,…}, тізбек мұнда әрбір қабырғаның бір төбесі g_k-1, болып, екінші g_k+1 қабырғаның төбесі болады

2. қабырғалардан түзілген шекті S={…, g₁,g₂,…}, тізбек

3. графтың төбелерінен түзілген { х₁,х₂…,х_n} тізбек

4. графтың төбелерінен және қабырғаларынан түзілген тізбек

5. графтың g_k қабырғасы, төбесіg_k+1 қабырғасы төбесінің біреуімен беттеседі.

$$42$$

1. Дана матрица инцидентности графа

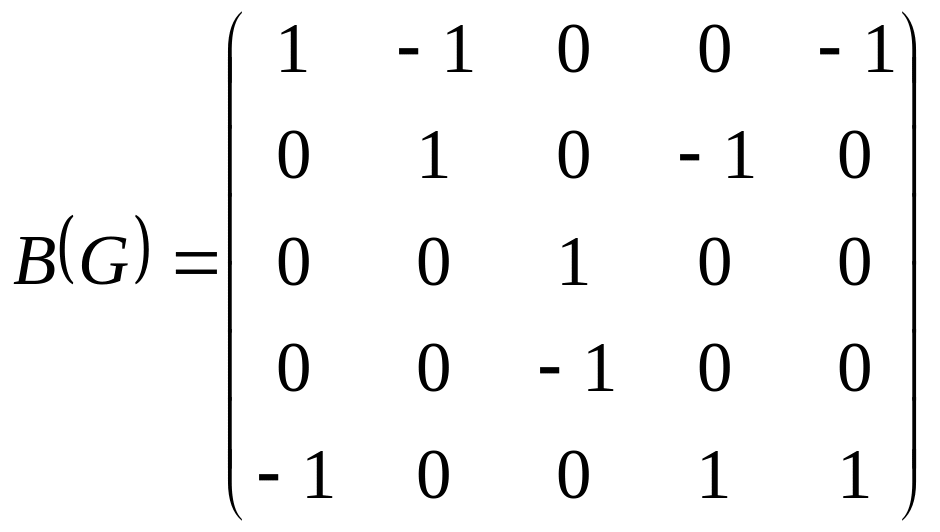
графтың түйiстiлiк матрицасы берiлген.

1. (5;1)

2. (1;2)

3. (4;3)

4. (2;5)

5. (1;5)

2. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. (1;2)

2. (5;1)

3. (4;3)

4. (2;5)

5. (1;5)

3. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. (4;3)

2. (5;1)

3. (1;2)

4. (2;5)

5. (1;5)

4. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. (2;5)

2. (5;1)

3. (4;3)

4. (1;2)

5. (1;5)

5. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. (1;5)

2. (5;1)

3. (4;3)

4. (2;5)

5. (1;2)

6. Из города А в город В ведет 3 дороги, а из города В в город С 7 – дороги. Сколькими способами можно добраться из А в С через В?

А қаласынан В қаласына3 жолмен, ал В қаласынан С қаласына 7 жолмен баруға болады. В қаласы арқылы А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 21

2. 15

3. 10

4. 6

5. 14

7. Из города А в город В ведет 2 дороги, а из города В в город С – 7 дорог; имеется также 3 дороги из А в С, не проходящих через В. Сколькими способами можно добраться из А в С ?

А қаласынан В қаласына 2 жолмен, ал В қаласынан С қаласына 7 жолмен баруға болады. А қаласынан С қаласына В дан өтпейтiн 3 жол бар. А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 17

2. 19

3. 18

4. 16

5. 15

8. Из города А в город В ведет 4 дороги, а из города В в город С – 2 дороги. Сколькими способами можно добраться из А в С через В?

А қаласынан В қаласына 4 жолмен, ал В қаласынан С қаласына 2 жолмен баруға болады. В қаласы арқылы А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 8

2. 5

3. 4

4. 7

5. 3

9. Из города А в город В ведет 3 дороги, а из города В в город С – 4 дорог. Сколькими способами можно добраться из А в С через В?

А қаласынан В қаласына 3 жолмен, ал В қаласынан С қаласына 4 жолмен баруға болады. В қаласы арқылы А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 12

2. 15

3. 10

4. 8

5. 14

10. Из города А в город В ведет 4 дороги, а из города В в город С – 4 дорог. Сколькими способами можно добраться из А в С через В?

А қаласынан В қаласына 4 жолмен, ал В қаласынан С қаласына 4 жолмен баруға болады. В қаласы арқылы А қаласынан С қаласына қанша әдiспен жетуге болады?

1. 16

2. 15

3. 10

4. 8

5. 14

$$43$$

1. Егер А = {1;2;3;4}; В = {2;3;4;5}; С = {1;2;3;4;5} болса,С жиынын таңдаңыз?

3. А\В

4. В\А

5. дұрыс жауабы жоқ

2. Егер А = {2;3;4;5;6}; В = {3;4;7}; С = {3;4} болса,С жиынын таңдаңыз?

2. А\В

3. В\А

5. дұрыс жауабы жоқ

3. Егер А = {3;4}; В = {1;2;3;4;}; С = {1;2} болса,С жиынын таңдаңыз?

1. В\А

3. А\В

5. дұрыс жауабы жоқ

4. Егер А = {2;3;4;7;8}; В = {3;4}; С = {2;7;8} болса,С жиынын таңдаңыз?

1. А\В

3. В\А

5. дұрыс жауабы жоқ

5. Егер А = {1;3;5;7;9}; В = {7;9}; С = {1;3;5} болса,С жиынын таңдаңыз?

1. А\В

3. В\А

5. дұрыс жауабы жоқ

6. Егер А = {1;2;3;4}; В = {2;3;4;5}; =?

1. {1;2;3;4;5}

2. {2;3;4}

3. {2;3;4;5}

4. {4;5}

5. {1;2;3}

7. Егер А = {2;3;4;5;6}; В = {3;4;7}; =?

1. {3;4}

2. {2;3;4}

3. {2;3;4;5;6}

4. {4;7}

5. {4}

8. Егер А = {3;4}; В = {1;2;3;4;}; В\А=?

1. {1;2}

2. 1;2}

3. 1;2}

4. 1;2}

5. 1;2}

9. Егер А = {2;3;4;7;8}; В = {3;4}; A/B=?

1. {2;7;8}

2. {7;8}

3. {2;7}

4. {2;3;7;8}

5. {8}

10. Егер А = {1;3;5;7;9}; В = {7;9}; A/B=?

1. {1;3;5}

2. {5}

3. {3;5}

4. {1;3;5;7:9}

5. {5;7;9}

$$44$$

1. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 0

4. 2

5. 4

2. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 0

2. 3

3. 1

4. 2

5. 4

3. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 2

4. 0

5. 4

4. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 1

4. 0

5. 4

5. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 1

2. 3

3. 0

4. 2

5. 4

6. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 4

2. 3

3. 5

4. 2

5. 4

7. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 3

2. 1

3. 0

4. 2

5. 4

8. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 5

4. 4

5. 6

9. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 4

2. 3

3. 5

4. 2

5. 6

10. Дана матрица инцидентности графа

графтың түйiстiлiк матрицасы берiлген.

1. 2

2. 3

3. 1

4. 0

5. 4

$$45$$

1. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 6

2. 3

3. 1

4. 2

5. 4

2. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 5

2. 3

3. 1

4. 2

5. 4

3. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 4

2. 3

3. 2

4. 5

5. 0

4. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 7

2. 3

3. 5

4. 2

5. 4

5. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 6

2. 3

3. 5

4. 2

5. 4

6. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 4

2. 3

3. 1

4. 2

5. 0

7. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 7

2. 3

3. 1

4. 2

5. 4

8. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 6

2. 3

3. 2

4. 5

5. 0

9. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 5

2. 3

3. 1

4. 2

5. 4

10. Дана матрица смежности графа

графтың сыбайластық матрицасы берiлген.

1. 6

2. 3

3. 5

4. 2

5. 4