Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Кузбасский государственный технический университет имени Т.Ф. Горбачева»
Кафедра Электропривода и автоматизации
А.В. Григорьев
Динамические свойства двигателя постоянного тока с независимым возбуждением
Рекомендовано для использования в учебном процессе
по курсу «Теория электропривода»
учебно-методической комиссией специальности 140604 «Электропривод
И автоматика промышленных установок и технологических комплексов»
Кемерово 2011
Рецензия
Рецензенты:
Семыкина И.Ю., доцент кафедры электропривода и автоматизации
Завьялов В.М., председатель УМК специальности 140604 «Электропривод и автоматика промышленных установок и технологических комплексов»
Григорьев Александр Васильевич. Динамические свойства двигателя постоянного тока с независимым возбуждением: метод. указания для лабораторных работ по дисциплине «Теория электропривода» [Электронный ресурс]: для студентов специальности 140604 «Электропривод и автоматика промышленных установок и технологических комплексов» / А.В. Григорьев - Электрон. дан. - Кемерово: КузГТУ, 2011. - 1 электрон. опт. диск (CD-ROM); зв.; цв.; 12 см. - систем. требования: Процессор Intel или AMD 500 МГц, ОЗУ 128 Мб; (CD-ROM - дисковод); мышь. - Загл. с экрана.
Учебное электронное издание предназначено для использования в лабораторном практикуме по курсу «Теория электропривода». В данных методических указаниях приведены основные сведения для расчета, моделирования и анализа динамических режимов работы двигателей постоянного тока с независимым возбуждением. В методических указаниях приводятся примеры структурных схем модели ДПТНВ в среде SCICOS и математическая модель ДПТНВ. Издание будет полезно студентам специальности 140604 и инженерам-электроприводчикам.
Содержание
1. Цель и задачи работы
Цель работы: изучение динамических свойств машин постоянного тока, работающих в двигательном режиме, на модели в среде визуального программирования SCICOS.
Задачи работы:
1. Получить навыки моделирования электромеханических систем при помощи средств вычислительной техники.
2. Получить практические навыки расчета параметров моделей ДПТНВ.
3. Изучить влияние параметров ДПТНВ на динамические свойства электропривода в целом.
2. Теоретические сведения
Модель ДПТ включает в себя модель обмотки возбуждения и модель цепи якоря. Модель обмотки возбуждения можно представить в виде следующего уравнения:
,
(1)
где uVM - напряжение возбуждения ДПТ; RVM - активное сопротивление обмотки возбуждения ДПТ, зависящее от схемы соединения обмоток полюсов; ΨVM - потокосцепление возбуждения ДПТ; iVM - ток, протекающий по обмотке возбуждения ДПТ.
В зависимости от схемы соединения катушек возбуждения машины постоянного тока потокосцепление может быть определено двумя способами:
Последовательное соединение: ΨVM = kSVMΦVM, kSVM = 2pwVM
|
Параллельно-последовательное соединение: ΨVM = kSVMΦVM, kSVM = pwVM /2
|
где wVM - число витков обмотки возбуждения ДПТ; ΦVM - поток полюса машины, создаваемый обмоткой возбуждения ДПТ; 2p - число полюсов машины; kSVM - коэффициент схемы соединения обмоток возбуждения.
Поток полюса машины постоянного тока зависит от тока, протекающего по обмоткам возбуждения. Эта зависимость в общем случае имеет нелинейный характер.
Перепишем выражение (1), выразив потокосцепление машины через поток полюса:
.
Теперь учтем, что поток полюса зависит от тока обмотки возбуждения:
.
Введем понятие индуктивности обмотки возбуждения ДПТ:
.
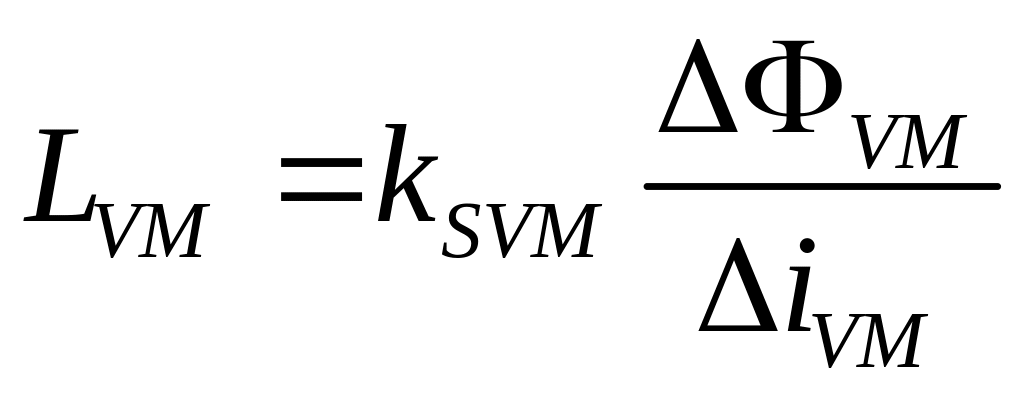Во многих работах зависимость потока полюса от тока обмотки возбуждения принимается линейной. В этом случае индуктивность обмотки возбуждения будет постоянна при любом токе обмотки возбуждения. Нелинейный характер зависимости потока полюса ДПТ от тока возбуждения незначительно сказывается на динамических процессах в случае работы с потоком, не превышающем номинального значения. В этом случае модель обмотки возбуждения генератора может быть выражена линейным дифференциальным уравнением:
.
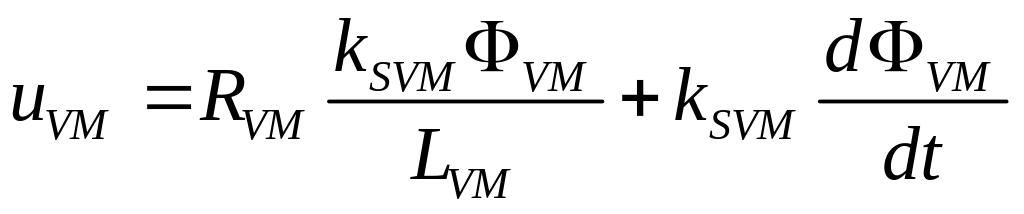То же самое, но в операторной форме:
,
где
;
- постоянная времени обмотки возбуждения
генератора.
При учете насыщения основной магнитной цепи удобно использовать среднеквадратичную аппроксимацию кривой намагничивания и кривой индуктивности. В обобщенном виде эта зависимость выражается таким образом:
Аппроксимация кривой, описывающей изменение индуктивности обмотки возбуждения в зависимости от тока обмотки возбуждения, представляется таким образом:
.
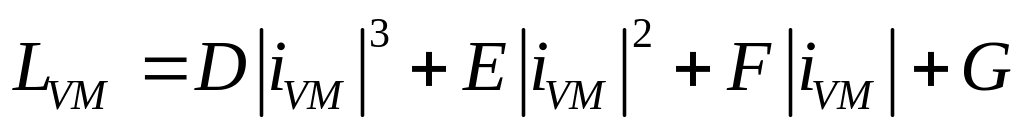Полученные зависимости составляют достаточно точную модель цепи возбуждения генератора. Структурная схема модели ДПТ при учете насыщения представлена на рис. 1 и при линейной зависимости потока от тока возбуждения – на рис. 2.
Рис. 1. Структурная схема цепи возбуждения ДПТ
при учете насыщения магнитной системы
Рис. 2. Структурная схема цепи возбуждения ДПТ
без учета насыщения магнитной системы
Представленные структурные схемы можно реализовать в среде разработки SCICOS, входящей в пакет SCICOSLab v.4.4 (рис. 3, 4).
Рис. 3. Окно программы SCICOS со структурной схемой цепи возбуждения двигателя постоянного тока при учете насыщения магнитной системы
Рис. 4. Окна настройки блоков Mathematical Expression
Модель якоря ДПТ можно получить из схемы замещения якорной цепи (рис. 5):
,
где Ua - напряжение, подводимое к якорю ДПТ; RaM = RКО + RДП + Ra - полное активное сопротивление якорной цепи ДПТ; LaM = LДП + LКО + La - полная индуктивность якорной цепи ДПТ; Ea = kMΦVMωM - ЭДС якоря ДПТ; kM=pN/2πa - конструктивный коэффициент ДПТ; ωM - частота вращения якоря ДПТ в рад/с.
Рис. 5. Принципиальная электрическая схема и схемы замещения ДПТ
Структурная схема ДПТ показана на рис. 6, где МПУ – механическое передаточное устройство электропривода, TaM = LaM / RaM.
Под действием подводимого к двигателю напряжения начинает протекать электрический ток в обмотке якоря. Ток якоря, взаимодействуя с магнитным потоком обмотки возбуждения, создает электромагнитный момент, способствующий вращению якоря ДПТ. При вращении якоря ДПТ под действием магнитного потока возбуждения образуется ЭДС вращения в обмотке якоря. ЭДС с ростом частоты вращения якоря приводит к уменьшению тока якоря, а, следовательно, и электромагнитного момента ДПТ до тех пор, пока не установится равновесие. Время разгона якоря ДПТ до установившейся скорости определяется суммарным приведенным моментом инерции нагрузки и самого двигателя J, а также моментом сопротивления нагрузки Мс.
Рис. 6. Структурная схема ДПТ при учете
насыщения магнитной системы