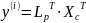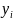- •Отчет по индивидуальному домашнему заданию
- •Содержание
- •Введение
- •Расчёты
- •Преобразование матрицы наблюдений путем центрирования исходных признаков
- •Построение ковариационной матрицы для исследуемого множества объектов
- •Набор собственных векторов матрицы ковариаций
- •Отображение распределения объектов заданных классов в пространстве новых признаков
Преобразование матрицы наблюдений путем центрирования исходных признаков
Выполним импорт данных из Excel в Mathcad, проделав следующие операции:
Вставка → Данные → Ввод из файла…
2) Задаём путь к файлу, выбираем нужный нам лист и диапазон ячеек.
Получим:


Центрирование производится по следующей формуле:
|

Для получения матрицы исходных данных произведём объединение двух классов:

Таблица 3. Матрица исходных данных

Отобразим полученную таблицу с помощью оператора ORIGIN.
Таблица 4. Матрица исходных данных с оператором ORIGIN
![]()


Рисунок 2 – График распределения исходных признаков
Вычислим средние значения столбцов:
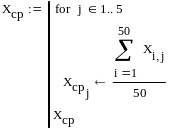
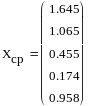
Выполним центрирование признаков:
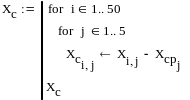

Построение ковариационной матрицы для исследуемого множества объектов
Ковариационная матрица вычисляется по следующей формуле:
|
Пример
расчёта элемента ковариационной матрицы:
ковариационной матрицы:
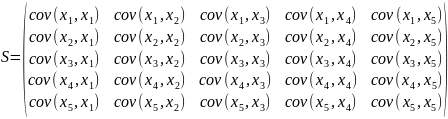 ,
,
где
 – дисперсии.
– дисперсии.
Вычислим ковариационную матрицу:
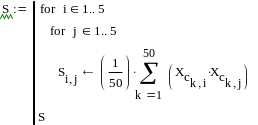

Набор собственных векторов матрицы ковариаций
Находим
собственные числа
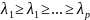 матрицы
матрицы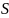 ,
как
вектор решений характеристического
уравнения:
,
как
вектор решений характеристического
уравнения:
, где |
S – матрица ковариаций; |
|
|
|
|
E – единичная матрица (квадратная матрица, элементы главной диагонали которой равны единице, а остальные равны нулю); |
||
|
Вычислим собственные числа и собственные векторы:
Таблица 5. Собственные числа и их векторы
Собственные числа:
|
Собственные вектора:
|
Таблица 6. Собственные вектора и их нормировка
Первый собственный вектор:
|
Второй собственный вектор:
|
Третий собственный вектор:
|
Четвёртый собственный вектор:
|
Пятый собственный вектор:
|
Нормировка векторов:
|
Переход от исходных центрированных признаков к главным компонентам
|
 –
–
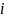 -ая
главная компонента.
-ая
главная компонента.
Определение новых координат объектов:
![]()
![]()
Построение кривой изменения относительной доли суммарной дисперсии, обусловленной первыми компонентами
|
–доля
дисперсии, вносимая первыми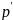 главными компонентами.
главными компонентами.
Таблица 7. Доли дисперсий для каждой главной компоненты
|
|
|
|
|
Из полученных данных построим график:
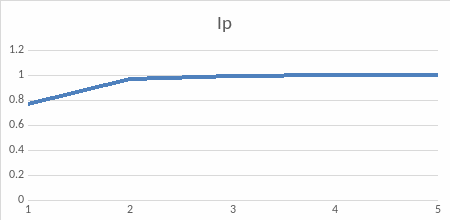
Рисунок 3 – Распределение дисперсии
Оценка доли дисперсии, которая обеспечивается первыми двумя главными компонентами
Произведём анализ дисперсий для двух главных компонент:
![]()
![]()
![]()
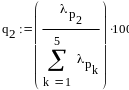
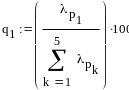
![]()
![]()
![]()
Таблица
8. Анализ вклада главных компонент
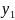 и
и

Главная
компонента
|
|
|
Собственное число |
0,2 |
0,054 |
Вклад главной компоненты, % |
76,726 |
20,605 |
Суммарный вклад, % |
76,726 |
97,321 |
Мы видим, что суммарный вклад двух компонент и от общей дисперсии составляет 97,321%, чего достаточно для дальнейшего анализа.

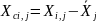
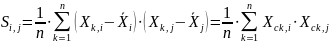
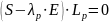
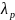 – собственное
число;
– собственное
число;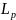 – собственный
вектор
– собственный
вектор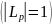 .
.