
- •Линейная алгебра
- •Содержание
- •Предисловие
- •Материалы к практическим занятиям
- •1.Матрицы и определители
- •1.1.Основные термины, формулы, положения
- •1.2. Типовые задания по теме
- •1.3. Дополнительные задания по теме
- •2. Решение систем линейных уравнений
- •2.1.Основные термины, формулы, положения
- •2.2. Типовые задания по теме
- •2.3.Дополнительные задания по теме
- •3. Арифметическое n-мерное пространство
- •3.1.Основные термины, формулы, положения
- •3.2. Типовые задания по теме
- •3.3. Дополнительные задания по теме
- •4. Векторные пространства Евклидовы пространства
- •4.1.Основные термины, формулы, положения
- •4.2. Типовые задания по теме
- •4.3.Дополнительные задания по теме
- •5. Линейные отображения векторных пространств
- •5.1.Основные термины, формулы, положения
- •4.2. Типовые задания по теме
- •5.3.Дополнительные задания по теме
- •6. Линейные математические модели в экономике
- •6.1.Основные термины, формулы, положения
- •6.2. Типовые задания по теме
- •6.3. Дополнительные задания по теме
- •7. Векторы на плоскости и в пространстве
- •7.1.Основные термины, формулы, положения
- •7.2. Типовые задания по теме
- •7.3. Дополнительные задания по теме
- •8. Уравнения линии на плоскости
- •8.1.Основные термины, формулы, положения
- •8.2. Типовые задания по теме
- •8.3. Дополнительные задания по теме
- •9. Уравнение плоскости и прямой в пространстве Поверхности второго порядка
- •9.1.Основные термины, формулы, положения
- •9.2. Типовые задания по теме
- •III. Примерные варианты контрольных работ Контрольная работа №1.
- •Контрольная работа №2
- •IV. Тестовые задания
- •V. Программа экзамена (зачета)
- •VI. Задачи для подготовки к экзамену (зачету)
- •VII. Литература
2. Решение систем линейных уравнений
2.1.Основные термины, формулы, положения
Линейное уравнение с n переменными. Система m линейных уравнений с n переменными (СЛУ). Вектор-решение СЛУ. Совместные СЛУ.
Основная и расширенная матрица СЛУ. Решение системы n линейных уравнений с n переменными в матричной форме.
Теорема Крамера. Решение СЛУ по формулам Крамера.
Равносильные СЛУ. Преобразования, приводящие к равносильной СЛУ. Метод Гаусса.
Однородные СЛУ. Свойства множества решений однородной СЛУ.
2.2. Типовые задания по теме
1. Решить СЛУ, если это возможно, в матричной форме и по формулам Крамера:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)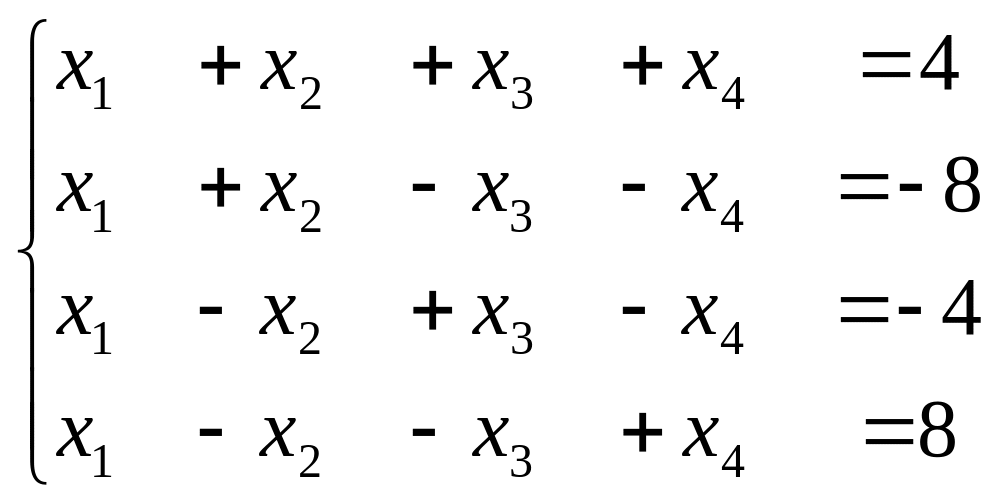 .
.
3. Решить систему
линейных уравнений, заданную в матричной
форме
![]() ,
если
,
если
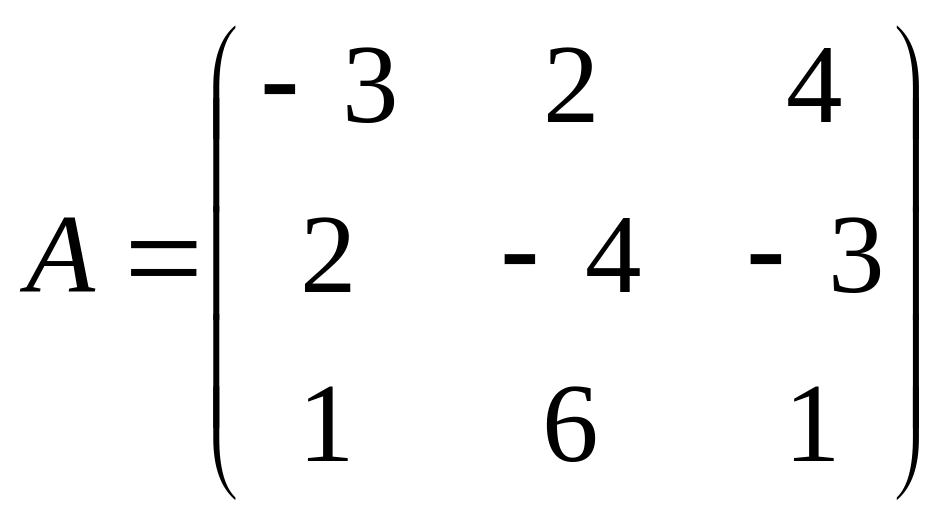 и
и
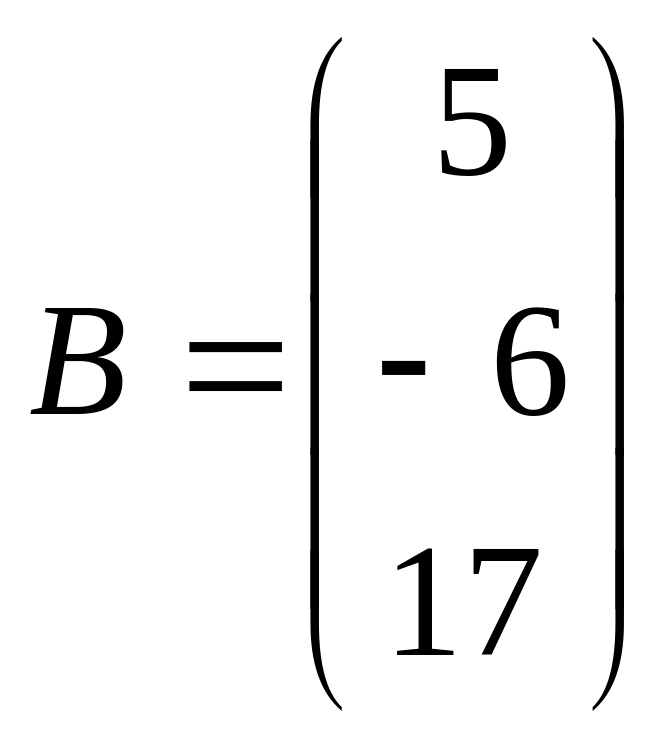 .
.
4. Решить системы линейных уравнений методом Гаусса:
а)
 ;
б)
;
б) ;
;
в)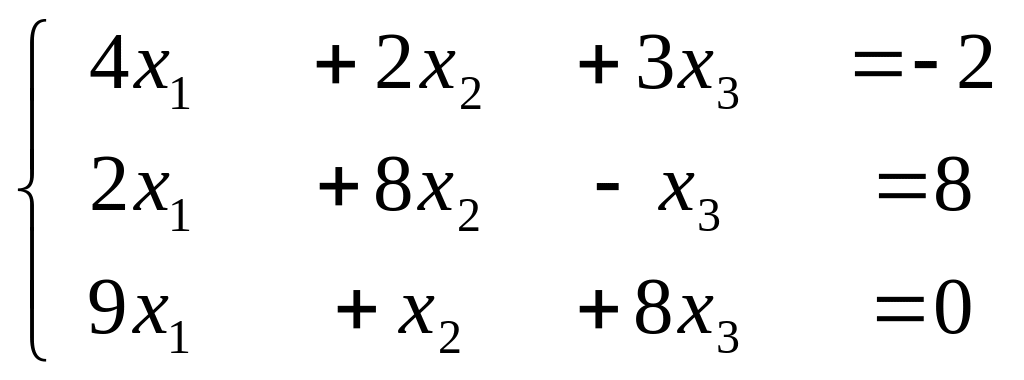 ;
г)
;
г)
д) ;
е)
;
е)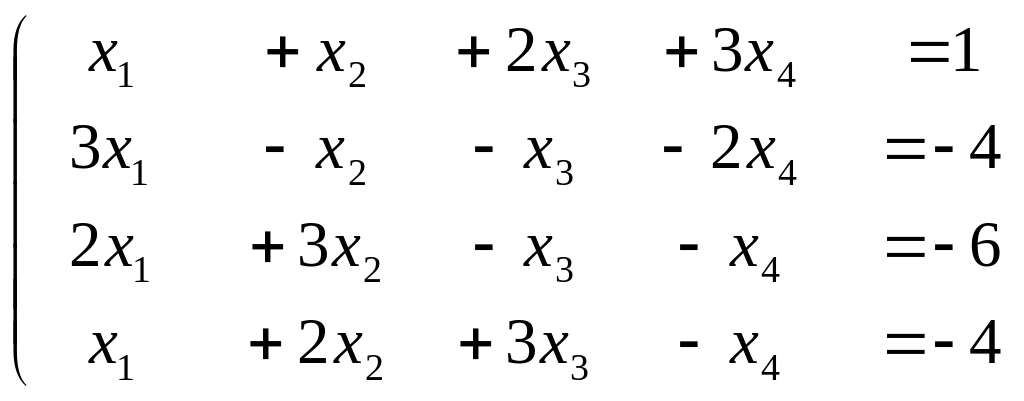 ;
;
ж) ;
з)
;
з)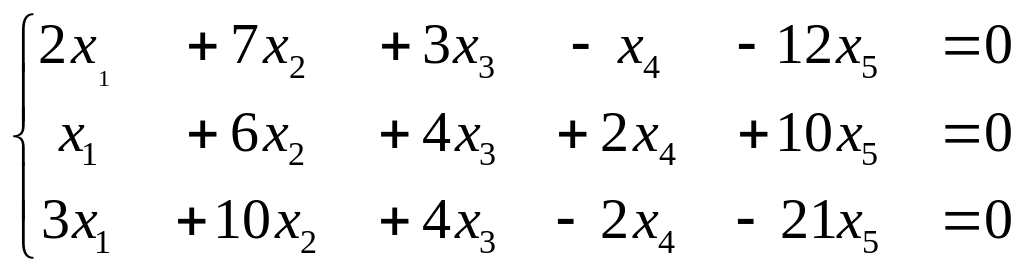 .
.
5. Швейная фабрика в течение трех дней производила костюмы, плащи и куртки. Известны объемы выпуска продукции за три дня и денежные затраты на производство за эти три дня:
-
День
объем выпуска продукции (ед)
затраты (тыс.усл.ед)
Костюмы
Плащи
Куртки
1
50
10
30
176
2
30
25
20
168
3
40
20
30
184
Найти себестоимость единицы продукции каждого вида.
2.3.Дополнительные задания по теме
1. Дана система
![]() ,
причем хотя бы один из определителей
,
причем хотя бы один из определителей
![]() ,
,
![]() ,
,
![]() отличен от 0. Доказать, что одно из решений
системы будет:
отличен от 0. Доказать, что одно из решений
системы будет:
![]() .
.
2. При каких значениях
a
система однородных уравнений
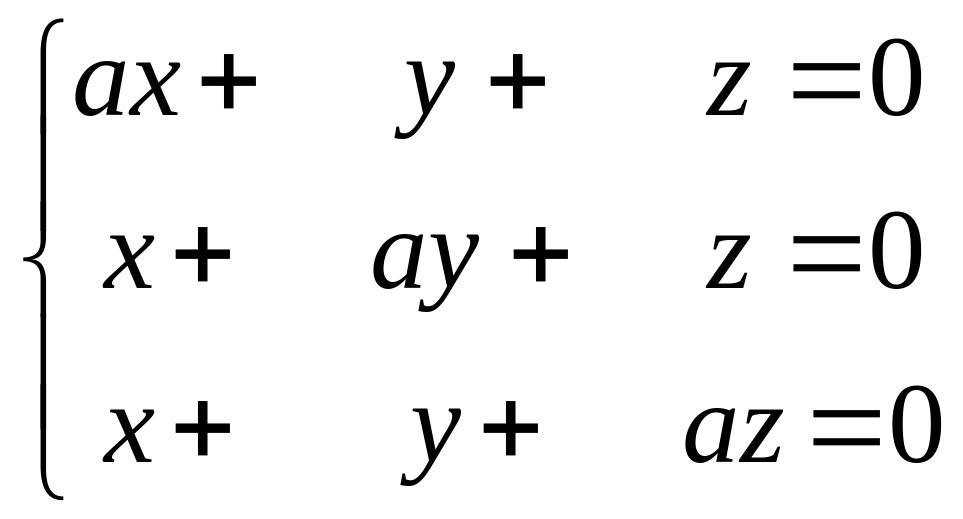 имеет ненулевое решение ?
имеет ненулевое решение ?
3. Найти квадратный
многочлен
![]() зная, что
зная, что
![]()
3. Арифметическое n-мерное пространство
3.1.Основные термины, формулы, положения
Арифметический n-мерный вектор. Линейные операции над арифметическими векторами, их свойства.
Линейная комбинация. Линейная зависимость системы векторов. Линейная независимость системы векторов. Базис системы векторов. Ранг системы векторов. Ранг матрицы.
Арифметическое n-мерное пространство: определение, базис, свойства. Разложение вектора по базису, Координаты вектора.
Приложения теории арифметического векторного пространства: критерий совместности системы линейных уравнений; пространство решений однородной системы линейных уравнений; фундаментальный набор решений.
3.2. Типовые задания по теме
1. Найти линейную комбинацию арифметических векторов:
а)
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() .
.
2. Найти вектор x
из уравнения
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() .
.
3. Будет ли данная система векторов линейно зависимой:
а)
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ,
,
![]() ;
;
в)
,
,
,
![]() ?
?
4. Доказать: а) система векторов, содержащая два равных вектора, линейно зависима; б) система векторов, два вектора которой различаются скалярным множителем, линейно зависима.
5. Образуют ли
векторы
![]() ,
,
![]() ,
,
![]() ,
,
![]() базис пространства R4?
базис пространства R4?
6. При помощи элементарных преобразований найти ранги матриц:
а)
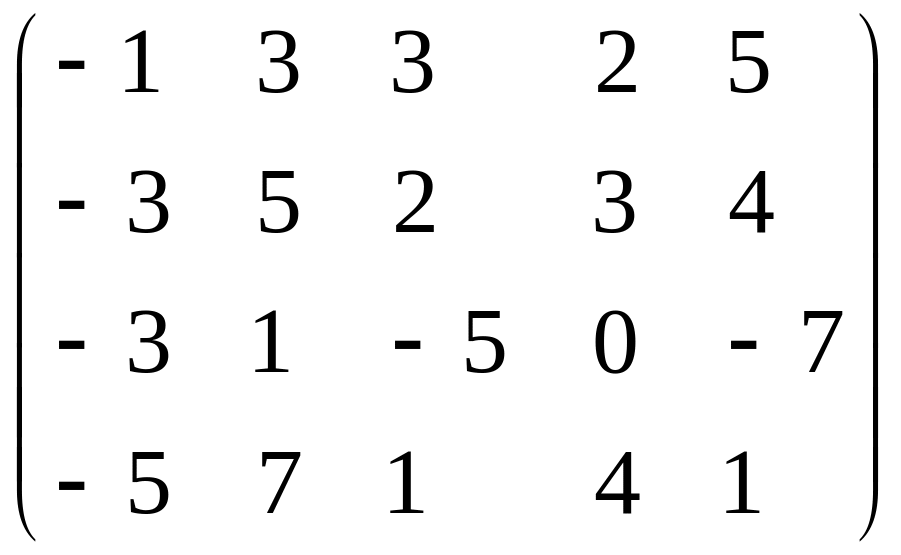 ;
б)
;
б)
 ;
в)
;
в)
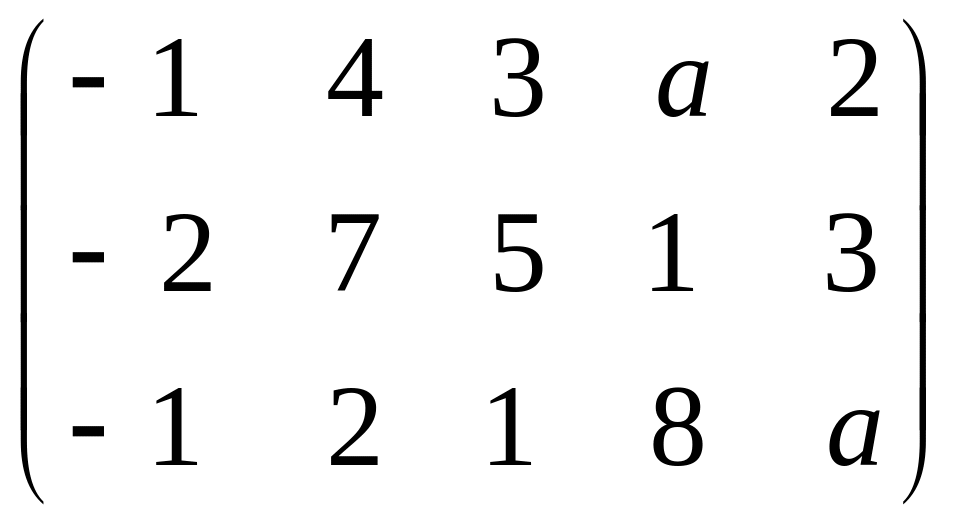
(в зависимости от а).
7. Как может измениться ранг матрицы, если приписать к ней: а) одну строку, б) две строки?
8. Исследовать на совместность системы линейных уравнений:
а) ;
б)
;
б)

9. Описать множество решений однородной СЛУ, используя фундаментальный набор решений:
а) ;
б)
;
б) ;
;
в) ;
г).
.
;
г).
.
10. Найти базис и
размерность векторного пространства
решений однородной СЛУ:
 .
.
11. Является ли
фундаментальным набором решений системы
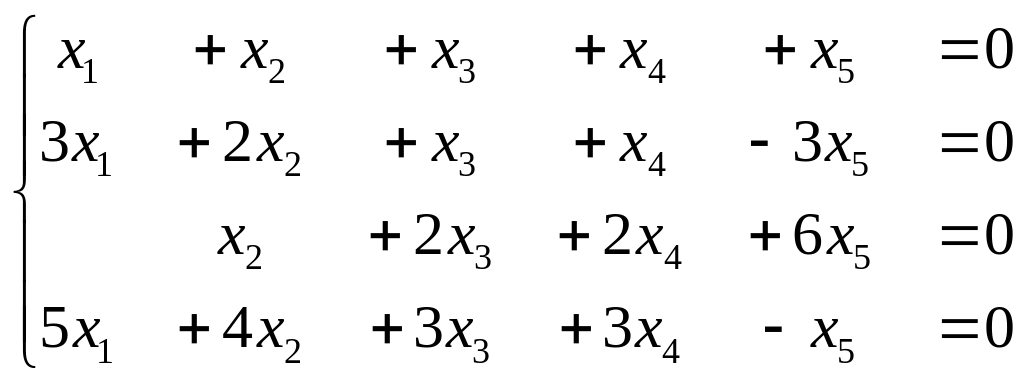 набор векторов:
набор векторов:
а)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
б)
,
,
![]() ?
?
12. Является ли
вектор
![]() решением системы
решением системы
 ?
?
Используя предыдущее задание №11, записать вектор общего решения для данной системы.
