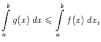- •Первообразная функции. Теорема о существовании первообразной функции.
- •Определение неопределенного интеграла, его свойства, геометрический смысл.
- •Методы нахождения неопределенных интегралов. Непосредственное интегрирование.
- •Метод неопределенного интегрирования заменой переменной. Метод неопределенного интегрирования подведением под знак дифференциала.
- •Интегрирование некоторых функций, содержащих квадратный трехчлен в знаменателе
- •Интегрирование неопределенных интегралов нескольких типов по частям.
- •Интегрирование дробно-рациональных функций. Разложение на простые дроби.
- •Методы интегрирования тригонометрических функций
- •Интегрирование иррациональных функций.
- •Интегрирование иррациональных функций с помощью тригонометрических подстановок.
- •Понятие определенного интеграла. Взаимосвязь неопределенного интеграла и определенного интегралов. Формула Ньютона-Лейбница. Свойства определенного интеграла.
- •1. Постоянный множитель можно выносить за знак интеграла
- •Задачи, приводящие к понятию определенного интеграла. Геометрический смысл определенного интеграла.
- •Методы интегрирования определенных интегралов заменой переменной и по частым.
- •Несобственные интегралы с бесконечными пределами.
- •Признаки сходимости несобственных интегралов.
- •Несобственные интегралы от разрывных функций.
- •Вычисление площадей плоских фигур с помощью интегралов.
- •Вычисление объемов тел вращения с помощью интегралов.
- •Вычисление длины дуги кривой
- •Численные методы вычисления определенного интеграла. Формулы прямоугольников и трапеций. Формула Симсона для вычисления неопределенных интегралов.
- •Двойные интегралы, их геометрический смысл, свойства. Вычисление двойных интегралов.
- •Дифференциал уравнения. Основные понятия. Нахождение уравнения по его решению
- •Дифференциальное уравнение первого порядка, его геометрический смысл. Задача Коши. Теорема о существовании и единственности решения дифференциального уравнения.
- •Задача Коши.
- •Дифференциальные уравнения с разделяющимися переменными и с однородными функциями.
- •А. Уравнение с разделенными переменными Уравнением с разделенными переменными называется уравнение вида:
- •Линейные дифференциальные уравнения, решение методом замены переменной и методом вариации произвольной постоянной.
- •А. Интегрирование линейного однородного уравнения
- •Линейные дифференциальные уравнения n-го порядка, свойства их решений. Линейные дифференциальные уравнения 2-го порядка.
- •Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Характеристическое уравнение. Вид общего решения однородного уравнения.
- •Экономические приложения интегралов
- •Если покупатель приобретает товар в количестве q* по равновесной цене p*, то очевидно, что общие расходы на покупку такого товара составят p*q*, что равно площади заштрихованной фигуры a (рис.2.4).
- •Таким образом, мы получим, что суммарные затраты потребителей при покупке товара мелкими партиями d q равны:
- •Так как величина d q очень мала, а функция f(q) непрерывна, то заключаем, что приблизительно равна площади фигуры b (рис.2.6) [5].
- •Площадь фигуры b при малых приращениях аргумента d q равна определенному интегралу от обратной функции спроса при изменении аргумента от 0 до q*, т. Е. В итоге получим, что:
- •Экономические приложения дифференциальных уравнений.
Несобственные интегралы от разрывных функций.
Несобственным интегралом второго рода назовём тогда интеграл
 значение
значение
 которого
равняется левостороннему пределу
которого
равняется левостороннему пределу
 Если
этот предел существует, то несобственный
интеграл называется сходящимся,
а если предела не существует, то
расходящимся.
Расходящемуся интегралу не приписывается
никакого числового значения; в этом
случае будем условно писать
Если
этот предел существует, то несобственный
интеграл называется сходящимся,
а если предела не существует, то
расходящимся.
Расходящемуся интегралу не приписывается
никакого числового значения; в этом
случае будем условно писать
 Геометрически
вычисление несобственного интеграла
второго рода представляет собою (при
Геометрически
вычисление несобственного интеграла
второго рода представляет собою (при
 )
исчерпание плошади неограниченной
фигуры под графиком функции
)
исчерпание плошади неограниченной
фигуры под графиком функции
 над
над
 с
помощью вычисления плошадей ограниченных
фигур, получающихся над отрезком
с
помощью вычисления плошадей ограниченных
фигур, получающихся над отрезком
 ,
а затем приближением правого конца
,
а затем приближением правого конца
 к
точке
к
точке
 (см. рис.).
(см. рис.).
 Итак,
площадь неограниченной фигуры,
изображённой на рисунке, по
определению
равна значению несобственного интеграла
Итак,
площадь неограниченной фигуры,
изображённой на рисунке, по
определению
равна значению несобственного интеграла
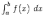 .
.
Аналогично
интегралу по полуинтервалу
от
функции
 с
особенностью в точке
,
определяется несобственный интеграл
второго рода от функции
с
особенностью в точке
,
определяется несобственный интеграл
второго рода от функции
 ,
имеющей особенность в точке
,
имеющей особенность в точке
 полуинтервала
полуинтервала
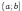 :
:
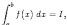 если
существует предел
если
существует предел
 В
случае существования указанного предела
интеграл называется сходящимся,
а в случае, когда предел не существует, --
расходящимся.
Свойства несобственных интегралов
второго рода
В
случае существования указанного предела
интеграл называется сходящимся,
а в случае, когда предел не существует, --
расходящимся.
Свойства несобственных интегралов
второго рода
Свойства
несобственных интегралов второго рода,
по сути дела, повторяют свойства
несобственных интегралов первого рода:
меняется лишь база предела, задающего
несобственный интеграл, с
 для
интеграла
для
интеграла
 на
на
 для
интеграла от функции с особенностью в
точке
:
для
интеграла от функции с особенностью в
точке
:
 Теорема
4.5 Пусть фиксированы
числа
Теорема
4.5 Пусть фиксированы
числа
 и
функция
и
функция
 интегрируема
на любом отрезке
,
где
интегрируема
на любом отрезке
,
где
 ,
и имеет особенность в точке
.
Тогда если несобственный интеграл
,
и имеет особенность в точке
.
Тогда если несобственный интеграл
 сходится,
то при любом
сходится,
то при любом
 сходится
интеграл
сходится
интеграл
 .
Обратно, если при некотором
.
Обратно, если при некотором
 сходится
интеграл
сходится
интеграл
 ,
то сходится и интеграл
,
то сходится и интеграл
 .
Доказательство. Докажем, что из
сходимости
следует
сходимость
.
Доказательство. Докажем, что из
сходимости
следует
сходимость
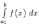 при
при
 .
Из аддитивности интеграла следует, что
при любом
имеет
место равенство
.
Из аддитивности интеграла следует, что
при любом
имеет
место равенство
|
(4.4*) |
Переходя
в этом равенстве к пределу при
 ,
получаем:
,
получаем:
|
|
причём
несобственный интеграл в правой части
сходится по условию теоремы, а интеграл
 --
постоянное слагаемое. Значит, предел,
задающий интеграл
,
существует и равен
--
постоянное слагаемое. Значит, предел,
задающий интеграл
,
существует и равен
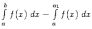 .
Докажем второе утверждение теоремы,
используя формулу (4.4*).
По условию теоремы интеграл по отрезку
.
Докажем второе утверждение теоремы,
используя формулу (4.4*).
По условию теоремы интеграл по отрезку
 ,
не содержащему особенностей функции,
существует, так что при любом
,
не содержащему особенностей функции,
существует, так что при любом
 из
формулы (4.4*)
получаем:
из
формулы (4.4*)
получаем:
|
|
Перейдём
к пределу при
 и
получим, что
и
получим, что
|
|
Теорема
4.6
(теоpема сpавнения) Пусть даны две
функции
 и
и
 ,
заданные на
и
имеющие особенность в точке
,
причём при всех
,
заданные на
и
имеющие особенность в точке
,
причём при всех
 выполняется
неравенство
выполняется
неравенство
 Тогда
из сходимости интеграла от большей
функции следует сходимость интеграла
от меньшей функции, причём
Тогда
из сходимости интеграла от большей
функции следует сходимость интеграла
от меньшей функции, причём
|
(4.5) |
а из расходимости интеграла от меньшей функции, следует расходимость интеграла от большей функции:

Теорему
4.6
можно использовать для исследования
сходимости интегралов, не вычисляя их
значений. Теорема
4.7
Пусть
функция
 имеет
особенность в точке
.
Если интеграл
имеет
особенность в точке
.
Если интеграл
 сходится,
то сходится также интеграл
сходится,
то сходится также интеграл причём
имеет место неравенство
причём
имеет место неравенство
 Определение
4.8
Пусть функция
обладает
теми же свойствами, что в предыдущей
теореме. Если несобственный интеграл
Определение
4.8
Пусть функция
обладает
теми же свойствами, что в предыдущей
теореме. Если несобственный интеграл
 сходится,
то несобственный интеграл
сходится,
то несобственный интеграл
 называется
абсолютно
сходящимся.
Если несобственный интеграл
расходится,
а несобственный интеграл
называется
абсолютно
сходящимся.
Если несобственный интеграл
расходится,
а несобственный интеграл
 сходится,
а несобственный интеграл
сходится,
а несобственный интеграл
 называется
условно
сходящимся.
Предыдущая теорема означает, что любой
абсолютно сходящийся интеграл является
сходящимся. Теорема
4.8
Пусть
для функции
называется
условно
сходящимся.
Предыдущая теорема означает, что любой
абсолютно сходящийся интеграл является
сходящимся. Теорема
4.8
Пусть
для функции
 ,
имеющей особенность в точке
,
имеющей особенность в точке
 и
интегрируемой на любом отрезке
и
интегрируемой на любом отрезке
 ,
где
,
где
 ,
существует мажоранта
,
существует мажоранта на
на
 ,
причём несобственный интеграл
,
причём несобственный интеграл
 сходится.
Тогда несобственный интеграл
сходится.
Тогда несобственный интеграл
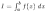 тоже
сходится, и
тоже
сходится, и
 .
.