1. Постоянный множитель можно выносить за знак интеграла

.

2. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций (верно для любого числа слагаемых):

.

3. При перемене порядка интегрирования знак определенного интеграла меняется на противоположный:

.

4. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b и с справедливо

.

5. Обе части неравенства можно почленно интегрировать, т.е. если для всех , то

.

6. Для определенный интеграл 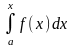становится функцией от переменного верхнего предела . Производная этой функции равна значению подынтегральной функции в точке :

.

7. Теорема о среднем. Если функция непрерывна на , то существует точка такая, что

.

Значение называется средним значением функции на .

у

В

А

Площадь криволинейной трапеции равна площади прямоугольника с основанием и высотой, равной значению функции в точке .

Геометрически теорема о среднем означает, что на отрезке найдется такая точка, что площадь под кривой на этом отрезке будет равна площади прямоугольника со сторонами и .

Формула Ньютона-Лейбница

Формула Ньютона-Лейбница связывает неопределенный и определенный интегралы.

Если функция непрерывна на , а функция - одна из ее первообразных, т.е. 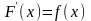, то определенный интеграл от функции f(х) на [а, b] равен приращению первообразной F(х) на этом отрезке, то есть

.

Эта формула сводит нахождение определенного интеграла к нахождению неопределенного интеграла.

Разность называется приращением первообразной и обозначается .

Подчеркнем, что при применении формулы Ньютона-Лейбница можно использовать любую первообразную для подынтегральной функции, например, имеющую наиболее простой вид при С = 0 (в дальнейшем не будем записывать константу при нахождении неопределенного интеграла, поскольку будем считать ее равной нулю).

Пример 1. Вычислить определенный интеграл .

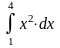Решение. По формуле Ньютона-Лейбница имеем

.

13. Задачи, приводящие к понятию определенного интеграла. Геометрический смысл определенного интеграла.

Геометрический смысл определенного интеграла

Понятие определенного интеграла введено таким образом, что в случае, когда функция y = f(x) неотрицательна на отрезке [a;b] и непрерывна на нем, где a < b,

численно равен площади S под кривой y = f(x) на [a; b] (рис. 3).

Рисунок. 3

Действительно, при стремлении к нулю ломаная (рис. 4) неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.

Рисунок. 4

Учитывая сказанное, можно указать значения некоторых интегралов, используя известные планиметрические формулы для площадей плоских фигур. Например,

и т.д.

(Первый из интегралов – площадь квадрата со стороной единичной длины; второй – площадь прямоугольного треугольника, оба катета которого единичной длины; третий – площадь четверти круга единичного радиуса).