9. Методы интегрирования тригонометрических функций

Интегралы вида , где R  рациональная функция,

приводятся к интегралу от рациональной функции путём замены , которая называется универсальной тригонометрической подстановкой. Это достигается тем, что и выражаются через рационально:

(1)

Пример 2. (воспользуемся формулами (1)) =

.

Замечание. Использование такой подстановки часто приводит к громоздким выражениям. Эта подстановка, как правило, эффективна, если и входят в дробное выражение в первой степени.

Интегралы вида с помощью подстановок: соответственно приводятся к интегралам от рациональной функции.

Пример 3.

.

Интегралы вида .

В этом случае применяется замена , так как и выражаются через рационально: , или используются тригонометрические формулы понижения степени.

Пример 4.

.

Интегралы вида , где среди показателей т и п по крайней мере одно нечетное.

В этом случае за новую переменную принимается та функция, которая содержит чётную степень, либо любая, если все функции в нечётных степенях.

Пример 5.

.

Интегралы вида .

Эти интегралы находятся с использованием формул:

Пример 6.

.

10. Интегрирование иррациональных функций.

Рассмотрим только некоторые частные случаи, когда интеграл от иррациональной функции выражается через элементарные функции.

Интегралы вида .

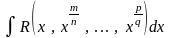Если , то подстановка имеет вид и тогда . После чего интегрирование сводится к интегрированию рациональных дробей.

Пример 1.

Замечание 1. Если выражение под знаком радикала линейное, т.е. имеет вид , то из свойства 4 следует, что мы вправе применить тот же подход.

Пример 2.

Интегралы вида .

Аналогично, если , то подстановка также приводит к интегрированию рациональных дробей.

Пример 3.

.

Интегралы вида .

Преобразуем выражение под знаком радикала. Если за знак радикала вынести , то получим . Выполнив замену , приходим к трём случаям:

11. Интегрирование иррациональных функций с помощью тригонометрических подстановок.

1. Интегралы вида .

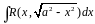Заменой такие интегралы приводятся к интегралам от рациональной функции.

Пример 3.

.

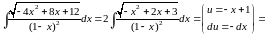
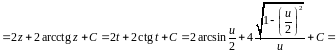
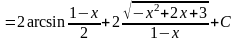2. Интегралы вида

В этом случае используется замена .

Пример 4.

.

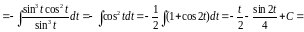
3. Интегралы вида .

Рационализация подынтегрального выражения достигается заменой .

Пример 5.

12. Понятие определенного интеграла. Взаимосвязь неопределенного интеграла и определенного интегралов. Формула Ньютона-Лейбница. Свойства определенного интеграла.

Пусть функция определена на отрезке . Разобьем отрезок на частей точками . Выберем на каждом из полученных отрезков произвольную точку .

Интегральной суммой функции на отрезке называется сумма

или

, где .

Наибольшую из длин обозначим через .

Определенным интегралом функции на отрезке называется число, равное пределу интегральной суммы и обозначается , т.е.

.

Из условия 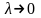следует, что .

Пределами интегрирования называются числа и .

Подынтегральной функцией называется функция .

Если функция непрерывна на отрезке , то определенный интеграл существует.

Подчеркнем, что определенный и неопределенный интегралы существенно различаются между собой. Если неопределенный интеграл представляет семейство функций, то определенный - есть определенное число.

Свойства определенного интеграла