6. Интегрирование некоторых функций, содержащих квадратный трехчлен в знаменателе

Рассмотрим интегралы вида . Они с помощью замены приводятся к известным интегралам.

Пример 1.

.

Замечание 1. Если для первого из рассмотренных интегралов квадрат-ный трёхчлен имеет действительные корни, то более целесообразно преобразовать подынтегральную функцию, представив её как сумму алгебраических дробей со знаменателями–множителями в разложении квадратного трёхчлена. Более подробно об этом будет рассмотрено в следующей лекции.

Пример 2. Найти интеграл .

Преобразуем подынтегральную функцию:

.

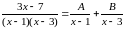Определим коэффициенты А и В, выполнив сложение дробей и приравняв числители дробей правой и левой частей равенства:

.

Приравнивая коэффициенты при х и свободные члены, получим

откуда .

Тогда имеем

7. Интегрирование неопределенных интегралов нескольких типов по частям.

Метод интегрирование по частям основан на формуле дифференцирования произведения двух функций.

Теорема. Пусть функции и определены и дифференцируемы на некотором промежутке . Пусть функция имеет первообразную на этом промежутке. Тогда функция 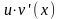тоже имеет первообразную на промежутке и справедлива формула

Доказательство. Из равенства

следует, что .

Первообразной функции на промежутке является функция . Функция имеет первообразную на , по условию теоремы. Следовательно, и функция имеет первообразную на . Интегрируя последнее равенство, получим формулу (1.12)

Формулу (1.12) называют формулой интегрирования по частям в неопределённом интеграле.

Поскольку , то формулу (1.12) можно записать в следующем виде

Эта формула сводит вопрос о вычислении интеграла к вычислению интеграла . В ряде конкретных случаев последний интеграл вычисляется без труда.

Большую часть интегралов, берущихся по частям, можно разбить на три основных группы:

I К первой группе относятся интегралы от функций, содержащих в качестве множителя одну из следующих функций:

Для вычисления интегралов этой группы следует применить формулу (1.12), положив в ней равной одной из указанных функций

Пример

Положим

Тогда

II Ко второй группе относятся интегралы вида

где - некоторые числа, - любое натуральное число.

Интегралы этой группы вычисляются путём применения формулы (1.12) раз. В качестве берётся функция .

Пример.

III К третьей группе относятся интегралы вида

.

Пример.

Для вычисления интеграла снова применим формулу (1.13): положим 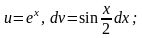тогда

Таким образом, в результате двукратного интегрирования по частям для данного интеграла I получим уравнение

Из этого уравнения получаем

8. Интегрирование дробно-рациональных функций. Разложение на простые дроби.

Нахождение интеграла сводится к интегрированию простейших дробей. Коэффициенты в числи-телях этих дробей вычисляются методом неопределённых коэффициентов.

Пример 1. .

Преобразуем подынтегральную функцию, представив её как сумму простейших дробей

.

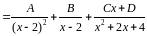Определим коэффициенты . Для этого приведём дроби в правой части равенства к общему знаменателя и приравняем числители дробей в правой и левой частей полученного равенства

.

Приравнивая коэффициенты при одинаковых степенях х (метод неопределённых коэффициентов), приходим к системе

Упростим систему, учитывая, что ,

Из первых двух уравнений получаем , из первого и третьего  и , .

Тогда наш интеграл приводится к нахождению интегралов

.
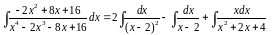