1. Первообразная функции. Теорема о существовании первообразной функции.

Пусть на промежутке определены функции и 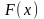, и во всех точках этого промежутка имеет место равенство

Тогда говорят, что функция есть первообразная функция, или просто первообразная функции на промежутке .

Теорема. («Единственность» первообразной). Если –

одна из первообразных функций для функции на промежутке , то любая первообразная функции на промежутке имеет вид , где - некоторая постоянная на промежутке функция.

Доказательство. Введём функцию 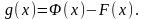Функция дифференцируема на промежутке как разность двух дифференцируемых функций, причём, всюду на

Тогда в силу следствия из теоремы Лагранжа функция постоянна на промежутке , т.е. , или , что и требовалось доказать.

Итак, если - первообразная функции на промежутке , то множество всех её первообразных совпадает с множеством , где - произвольная постоянная на промежутке функция.

Итак, первообразная данной функции на данном промежутке единственна с точностью до постоянного слагаемого.

2. Определение неопределенного интеграла, его свойства, геометрический смысл.

Множество всех первообразных данной функции называют неопределённым интегралом функции и обозначают символом

Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

.

2. Производная неопределенного интеграла равна подынтегральной функции:

.

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

.

4. Постоянный множитель можно выносить за знак интеграла:

, а − постоянная.

5. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) их неопределенных интегралов:

.

6. Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой от нее функции.

Если , то и , где .

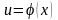Геометрическая интерпретация первообразной

Пусть функция непрерывна и неотрицательна на отрезке .

Рис. 1.2.

Рассмотрим криволинейную трапецию , изображённую на рис. 1.2. Определим на отрезке функцию следующим образом: каждому значению 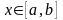поставим в соответствие величину площади криволинейной трапеции , заключённой между начальной ординатой и ординатой, отвечающей значению .

Найдём производную функции . Придадим переменной некоторое приращение : , 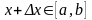. В силу непрерывности функция достигает на отрезке своих наименьшего и наибольшего значений. Очевидно, площадь заключена между площадями прямоугольников, построенных на основании и имеющих высоты и , т.е.

, откуда .

Если значения и будут изменяться и в силу непрерывности функции Поэтому

.

Среди первообразных функции на отрезке первообразная выделяется тем, что она обращается в в точке . Поэтому

В частности, площадь 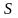криволинейной трапеции вычисляется по формуле