5.3. Теорема чебышева

Теорема Чебышева – одна из простейших, но наиболее важных форм закона больших чисел.

Рассмотрим случайную величину X, закон распределения которой от эксперимента к эксперименту изменяется. Тогда будем иметь дело с несколькими (n) случайными величинами.

Теорема 5.3. (теорема Чебышева). Если X₁, X₂,…, X_n,… независимые случайные величины с конечными математическими ожиданиями ,и дисперсиями ограниченными одним и тем же числом С, т.е. , то при возрастании n среднее арифметическое наблюденных значений величин , сходится по вероятности к среднему арифметическому их математических ожиданий, т.е. для любого >0

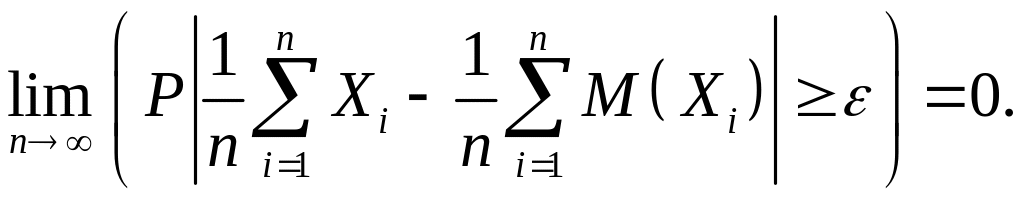_(5.5)

Д о к а з а т е л ь с т в о. Рассмотри величину . Ее математическое ожидание , а дисперсия . Применяя к величине Y неравенство Чебышева, получаем

или

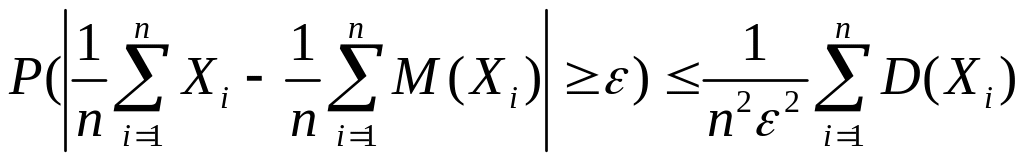
Так как , т о

. (5.6)

Как бы ни было мало >0, переходя к пределу в формуле (5.6) при n→∞, получим

,

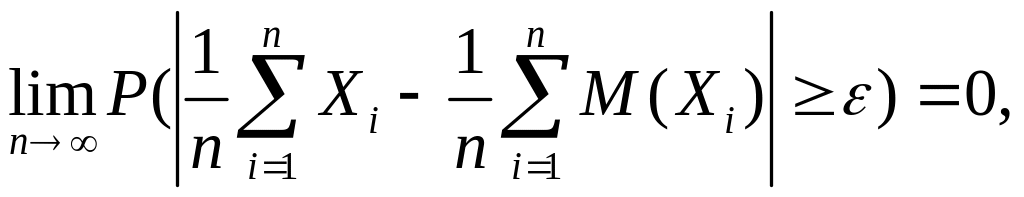что и требовалось доказать.

Из теоремы следует, что среднее арифметическое достаточно большого числа независимых переменных случайных величин (дисперсии которых равномерно ограничены) перестает быть случайной величиной, т.е. оно является устойчивым и сходится по вероятности к определенной неслучайной величине, так как среднее арифметическое математических ожиданий 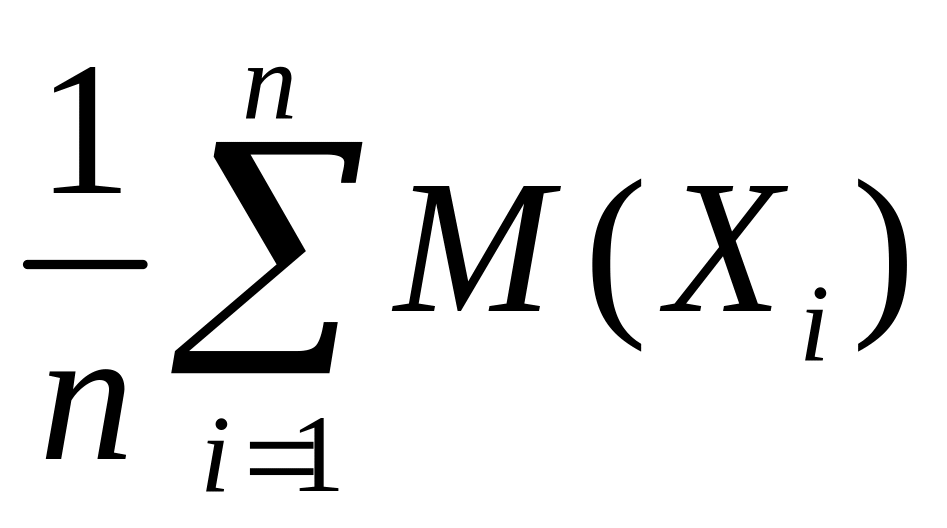- величина неслучайная.

Если в формуле (5.5) перейти к вероятности противоположного события, получим другую формулировку закона больших чисел:

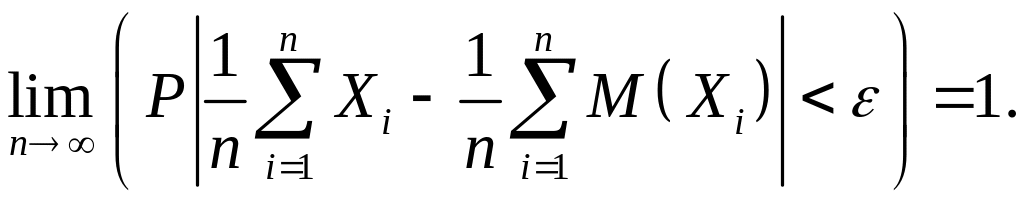
Частным случаем теоремы Чебышева для одинаково распределенных случайных величин , является

Теорема 5.4 (теорема Хинчина). Пусть X₁, X₂,… - независимые, одинаково распределенные случайные величины, имеющие конечные математические ожидания . Тогда последовательность , где , сходится к m с вероятностью 1, т.е. для любого >0

.

Закон больших чисел может быть распространен и на зависимые случайные величины.

Теорема 5.5 (теорема Маркова). Если для случайных величин X₁, X₂,…

,

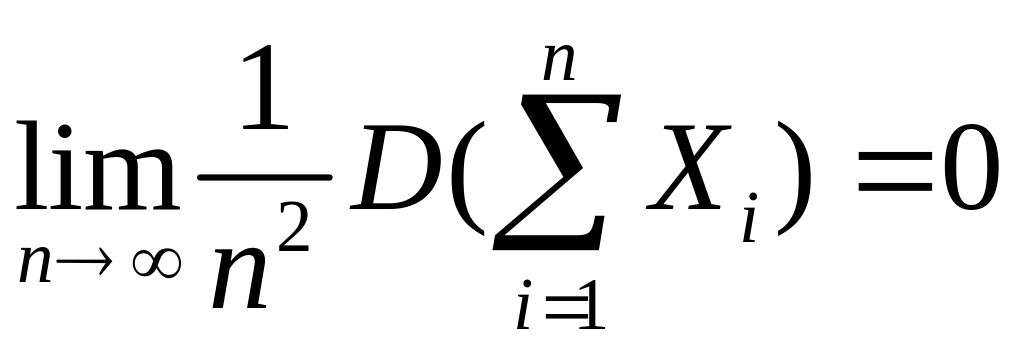то среднее арифметическое наблюденных значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:

для любого >0.

Неравенство Колмогорова (см. теорему 5.2) позволяет доказать теорему Колмогорова, в которой приведены достаточные условия для осуществления усиленного закона больших чисел:

последовательность случайных величин X₁, X₂,…, X_n,… подчиняется усиленному закону больших чисел, если с вероятностью 1 при n→∞ выполняется предельное соотношение

.

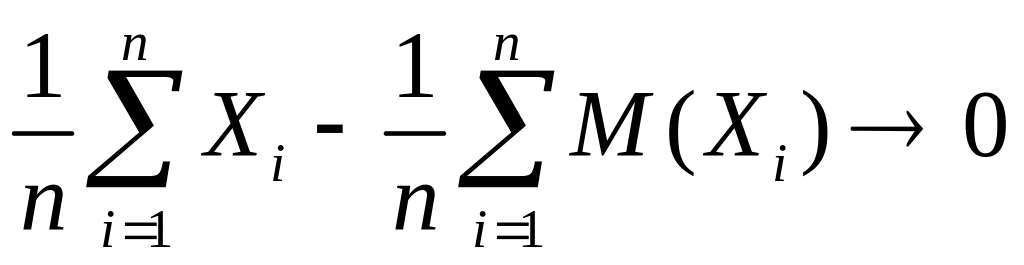Теорема 5.6 (теорема Колмогорова). Если последовательность взаимно независимых случайных величин X₁, X₂,…, X_n,… удовлетворяет условию

,

то она подчиняется усиленному закону больших чисел.

Из теоремы Колмогорова следует утверждение: существование математического ожидания является необходимым и достаточным условием для применимости усиленного закона больших чисел к последовательности одинаково распределенных и взаимно независимых случайных величин.

Усиленный закон больших чисел имеет большое принципиальное значение, так как, согласно этому закону, существует лишь конечное число случаев, когда среднее арифметическое случайных величин будет отличаться от среднего арифметического математических ожиданий.

Вопросы для самопроверки

1. При каких условиях среднее арифметическое наблюденных значений величин , сходится по вероятности к среднему арифметическому их математических ожиданий?

2. Какая теорема является частным случаем теоремы Чебышева? Сформулируйте ее.

3. Сформулируйте закон больших чисел для зависимых случайных величин.