5. Предельные теоремы теории вероятностей

Математические законы теории вероятностей получены абстрагированием реальных статистических закономерностей, свойственных массовым случайным явлениям, которые порождают в своей совокупности случайную величину, подчиненную вполне определенному закону. Массовые случайные явления – рассматриваются как последовательности экспериментов, происходящих при сохраняющемся комплексе условий , или большое число случайных воздействий. Это означает, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате массы таких явлений. Устойчивость средних и представляет собой физическое содержание закона больших чисел. В теории вероятностей под законом больших чисел понимается ряд математических теорем, в каждой из которых при тех или иных условиях устанавливается факт приближения средних характеристик большого числа экспериментов к некоторым вполне определенным постоянным. Свойство случайных величин в определенных условиях вести себя практически как неслучайные позволяет предсказывать результаты массовых случайных явлений почти с полной определенностью.

Возможности таких предсказаний в массовых случайных явлениях расширяются наличием предельных теорем, касающихся предельных законов распределения. Мы уже говорили, что закон распределения суммы достаточно большого числа случайных величин неограниченно приближается к нормальному распределению при соблюдении некоторых условий, которые содержатся в центральной предельной теореме.

Различные формы закона больших чисел вместе с различными формами центральной предельной теоремы образуют совокупность предельных теорем теории вероятностей.

С некоторыми из них мы уже познакомились.

Так, например, в гл. 2 доказывалось, что при n→∞ p_n→0 таким образом, что np_n= , где – фиксированное неотрицательное число, распределение случайной величины сходится к распределению Пуассона

т.е. случайная величина Х рассматривалась как сумма независимых случайных величин Х, имеющих множество значений , и эта сумма аппроксимировалась распределением Пуассона.

При изучении предельных теорем будем рассматривать различные виды сходимости случайных величин.

5.1. Сходимость случайных величин

Рассмотрим различные определения понятия предела в теории вероятностей.

Пусть на вероятностном пространстве (Ω, ,P) определена последовательность случайных величин X₁(ω), X₂(ω),…, X_n(ω),… Для каждого значения Ω получаем числовые последовательности:

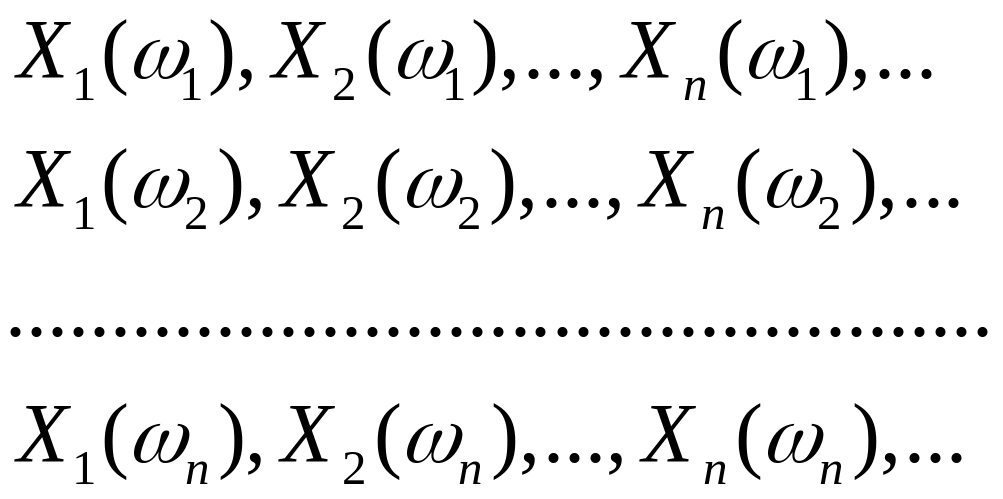
которые могут сходиться или расходиться. Множество элементарных событий ω_j , для которых соответствующие числовые последовательности сходятся, образует некоторое событие А Ω.

Тот факт, что последовательность сходится на множестве А Ω, будем записывать: для любых ω А, где случайная величина X(ω) определена на том же вероятностном пространстве (Ω, ,P).

Если вероятность множества тех

ω Ω, для каждого из которых числовая последовательность сходится к Х(ω), то последовательность сходится к Х(ω) с вероятностью 1.

Наиболее часто употребляется понятие сходимости по вероятности.

Определение 5.1. Последовательность случайных величин сходится к случайной величине Х(ω) по вероятности и обозначается , если для любого >0

Следовательно, вероятность того, что X_n отличается от X меньше любой заданной величины, близка к единице при достаточно больших значениях n.

Определение 5.2. Последовательность случайных величин сходится к случайной величине X по распределению и обозначается , если для любой точки x, в которой функция F(x) непрерывна .

Функция F(x) непрерывна в точке x в том и только в том случае, если .

Сходимость по распределению используется при аппроксимации одного распределения другим. Примером может служить сходимость биномиального распределения к пуассоновскому, о которой упоминалось выше.

Сходимость по распределению не налагает никаких требований на совместное распределение случайных величин и X.

Следует отметить, что из сходимости по вероятности следует сходимость по распределению , а из сходимости по распределению в общем случае не следует сходимость по вероятности. Сходимость по вероятности и сходимость с вероятностью 1 рассматривается в теоремах закона больших чисел и усиленного закона больших чисел.