28) Кинетическая энергия твердого тела при поступательном, вращательном и плоскопараллельном движении

1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости дви­жения центра масс. То есть, для любой точки V_i=V_C

или

Таким образом, кинетическая энергия тела при поступатель­ном движении равна половине произведения массы тела на квад­рат скорости центра масс. От направления движения значение энергии не зависит.

2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (1 рисунок), то скорость любой его точки   где  – расстояние точки от оси вращения, а  – угло­вая скорость тела.

Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Окончательно:

т.е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение энергия не зависит.

П ри вращении тела вокруг неподвижной точки кинетическая энергия определяется как

или

где   – моменты инерции тела относительно главных осей инерции x₁, y₁, z₁  в неподвижной точке О;    – проекции вектора мгновенной угловой скорости   на эти оси.

3. Плоскопараллельное движение. При этом движе­нии скорости всех точек тела в каждый момент времени распреде­лены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр ско­ростей Р (1 рисунок). Следовательно

где  - момент инерции тела относительно названной выше оси,  - угловая скорость тела. Величина   в формуле будет перемен­ной, так как положение центра Р при движе­нии тела все время меняется. Введем вместо   постоянный момент инерции , относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса-Штейнера   , где d=PC. Подставим это выражение для . Учитывая, что точка Р - мгновенный центр скоростей, и, следовательно,  , где  - скорость центра масс С, окончательно найдем:

Следовательно, при плоскопараллельном движении кинетиче­ская энергия тела равна энергии поступательного движения со скоростью центра масс, сло­женной с кинетической энергией вращательного движения вокруг центра масс.

29) Элементарная работа силы. Работа силы на конечном перемещении точки её приложения. Мощность силы

Работа силы, мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения. Cила F численно и по направлению постоянна, а перемещение M₀M₁ прямолинейно/ A = F×s×cosa, где s = M₀M₁, α – угол между направлениями силы и перемещения. Единицы измерения A: джоуль kbи килограмм-сила на метр (1 кгс×м). В общем случае для вычисления работы силы силы вводится понятие элементарной работы dA = F×ds×cosa, где ds – элементарное перемещение, α – угол между направлениями силы и касательной к траектории точки её приложения, направленной в сторону перемещения. В декартовых координатах dA = F_xdx + F_ydy + F_zdz, где F_x, F_y, F_z – проекции силы на координатные оси, х, у, z – координаты точки её приложения. Для сил, действующих на тело, имеющее неподвижную ось вращения, dA = M_zdj, где M_z – сумма моментов сил относительно оси вращения, j – угол поворота. Для сил давления dA = pdV, где р – давление, V – объём. Работа силы на конечном перемещении определяется как интегральная сумма элементарных работ и при перемещении M₀M₁ выражается к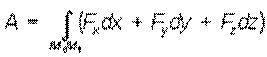 риволинейным интегралом:

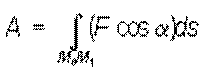
или

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность

где t - время, в течение которого произведена работа A. В общем случае

Следовательно, мощность равна произведению касательной состав­ляющей силы на скорость движения.

Единицей измерения мощности в системе СИ является ватт (1 вт=1 дж/сек).