16. Теорема об изменении количества движения материальной точки в дифференциальной и конечной формах.

• В дифференциальной форме:

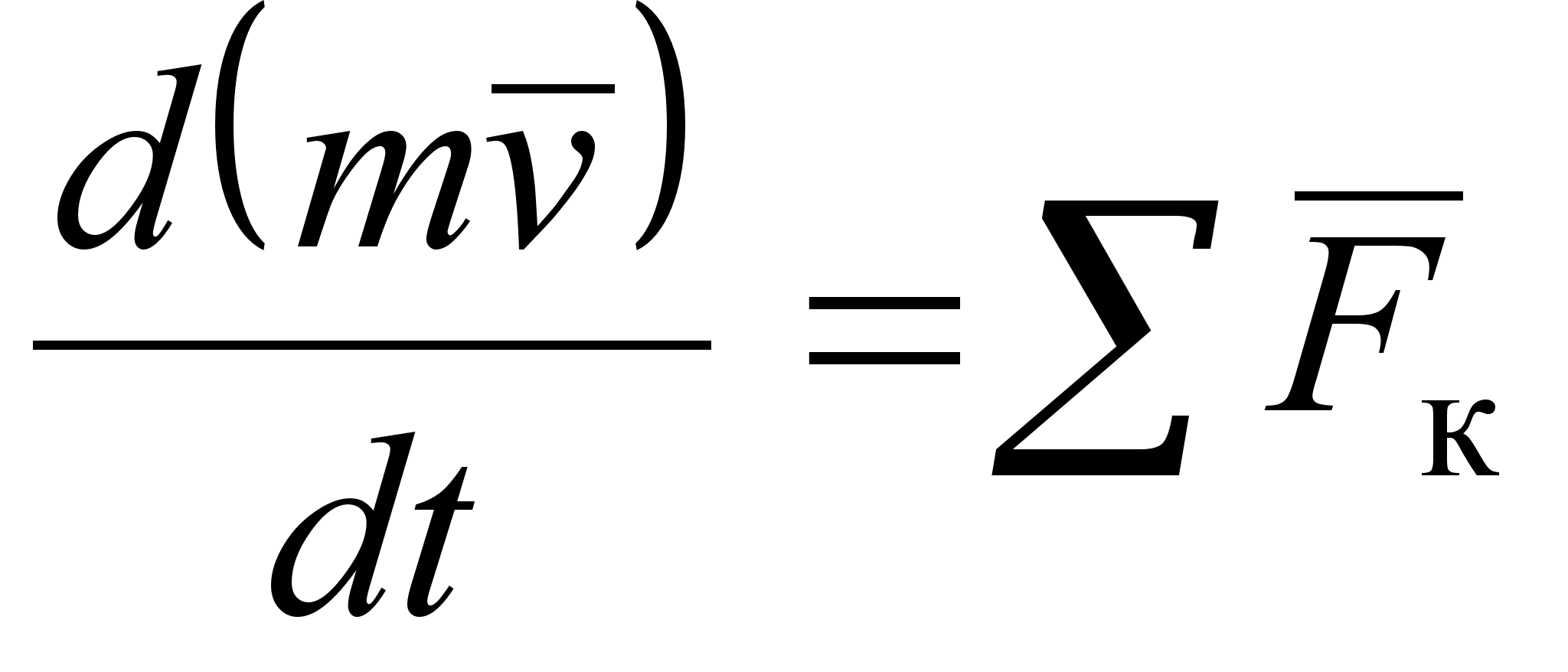
• В интегральной и конечной:

Где S_k – элементарный импульс силы

17. Главный вектор количества движения механической системы.

Количеством движения (главным вектором количества движения) механической системы называется вектор Q, равный геометрической сумме (главному вектору) количества движения точек системы:

Или массе системы, умноженной на скорость ее центра масс

Следовательно, если центр масс остается неподвижным, то количество движения системы равно нулю, значит при вращении вокруг оси, проходящей через центр масс, количество движения будет равно нулю.

Называют главным вектором, а не равнодействующей, потому что векторы скоростей точек системы лежат не в сходящейся системе.

18. Теорема об изменении количества движения механической системы

«Изменение количества движения системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, действующих на систему за тот же промежуток времени».

В диф. форме:

В конечной форме:

19. Закон сохранения количества движения системы

Это следствие из теоремы об изменении количества движения системы: «Если главный вектор внешних сил равен нулю, то количество движения механической системы будет постоянным»

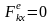
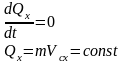
20. Момент количества движения материальной точки относительно центра и оси.

Моментом количества движения материальной точки относительно произвольного центра О называется вектор определяемый равенством

где r – радиус-вектор мат. точки, проведенный из центра О.

21. Кинетический момент механической системы относительно центра и оси.

Кинетический момент характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Главным вектором момента количества движения механической системы (кинематическим моментом) относительно произвольного центра О называется векторная величина равная сумме векторов моментов количеств движения всех точек системы

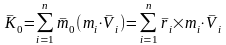
Спроецируем, данное векторное равенство на декартовы оси:

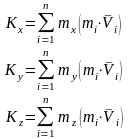
Покажем, что главный момент количества движения системы является характеристикой её вращательного движения:

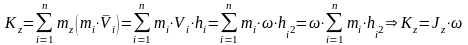
Следовательно, кинетический момент вращающегося тела относительно оси вращения равен произведению осевого момента на угловую скорость.

22. Кинетический момент вращающегося твердого тела относительно оси вращения.

Пусть твердое тело вращается вокруг неподвижной оси O_z с угловой скоростью 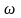. Выберем произвольную точку m_i в твердом теле и вычислим кинетический момент этого тела относительно оси вращения. По определению кинетического момента системы относительно оси имеем

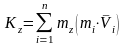
Но при вращении тела вокруг оси ,

причём количество движения точки m_i (m_iV_i) ­ перпендикулярно отрезку h_i и находится в плоскости, перпендикулярной оси вращения O_z. Следовательно, момент количества движения относительно оси O_z для точки m_i: .

Для всего тела: ,

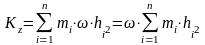то есть

Кинетический момент вращающегося тела относительно оси вращения равен произведению угловой скорости тела на его момент инерции относительно оси вращения.