Динамика

1. Дифференциальные уравнения движения материальной точки в векторной форме.

2) Дифференциальные уравнения движения материальной точки в декартовых координатах.

3) Естественные уравнения движения материальной точки.

4) Две задачи динамики материальной точки.

5) Решение второй задачи динамики точки. Определение постоянных интегрирования.

Второй или обратной называется задача, в которой по заданным силам и массе материальной точки определяется ее движение. Для решения задачи надо выполнить следующие операции.

● Построить расчетную схему. Для этого прежде всего надо выбрать систему координат. В случае произвольного движения точки в пространстве следует выбрать систему координат  . Положение начала координат   указывается в условии задачи или выбирается в начальном положении движущейся материальной точки.

● Затем в принятой системе координат надо изобразить предполагаемую траекторию точки и отметить на ней начальное положение точки  , изобразить начальную скорость  . Следует отметить также произвольное положение точки  , обозначить ее координаты  ; изобразить все силы, действующие на материальную точку в этом произвольном положении. Если точка движется по плоскости, то следует выбирать систему координат  . Для прямолинейного движения материальной точки достаточно выбрать одну координатную ось, которая совмещается с траекторией точки; при этом за положительное направление оси следует принять направление начальной скорости  .

Уточнить начальные условия движения точки, т. е. из условия задчи при   определить   – координаты точки в начале движения;   – проекции начальной скорости на оси координат.

Составить дифференциальные уравнения движения точки в форме (1.2):

– это  дифференциальные уравнения второго порядка.

Определить законы движения вдоль координатных осей; т. е. найти вторые интегралы уравнений (1.2):

Постоянные интегрирования   находятся с использованием начальных условий обычными для теории дифференциальных уравнений способами.

Основные виды дифференциальных уравнений и их интегрирование даны в приложении.

6) Дифференциальные урав-я относит-го движения матер-ой точки.

Составим основное уравнение динамики для точки , где абсолютное ускорение . Поэтому уравнение будет таким .

Но - переносная сила инерции, - кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так

Спроектировав это векторное равенство на подвижные оси x1, y1, z1, имея в виду, что проекции вектора ускорения на оси – есть вторые производные от соответствующих координат по времени, получим дифференциальные уравнения относительного движения:

7. Принцип относительности классической механики.

8. Классификация сил мех системы. Свойство внутр сил

Силы, действующие на точки механической системы можно разделить на внешние и внутренние.

Внешними (F_i^E) называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними (F_i^I) называют силы, с которыми точки или тела одной системы действуют друг на друга.

Внутренние силы обладают следующими свойствами:

1.Геометрическая сумма всех внутренних сил системы равняется нулю. На основании третьего закона Ньютона силы взаимодействия между точками (телами) равны и противоположно направлены, следовательно, и сумма этих сил равна нулю (∑F_i^I=0). 

2.Сумма моментов ( главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю.На основании теоремы Вариньона и главный момент внутренних сил относительно произвольного центра также равен нулю ( ∑M_i0F_i^I=0 ).

Из доказанных свойств не следует, однако, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызвать взаимные перемещения этих точек или тел. Уравновешенной вся совокупность внутренних сил будет у системы, представляющей собой абсолютно твердое тело.

9. Момент инерции тела относительно оси. Радиус инерции.

10. Теорема о моментах инерции тела относительно параллельных осей.

11. Моменты инерции однородного тонкого стержня, однородного тонкого кольца (тонскостенного полого цилиндра), сплошного кругового цилиндра (диска ).

12) Диффер-ые урав-я движения механической системы в векторной форме и в проекциях на декартовые оси.

Рассмотрим систему, состоящую из n материальных точек. Выделим какую-нибудь точку системы с массой . Обозначим равнодействующую всех приложенных к точке внешних сил (и активных и реак­ций связей) через , а равнодействующую всех внутренних сил – через . Если точка имеет при этом ускорение , то по основному закону динамики

......

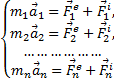
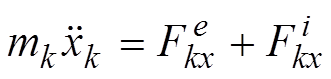13) Теорема о движении центра масс механической системы.

Теорема о движении центра масс механической системы: центр масс механической системы движется как материальная точка с массой, равной массе системы, под действием главного вектора внешних сил, действующих на эту механическую систему.

14) Количество движений материальной точки.

Количество движения мера механического движения, равная для материальной точки произведению её массы m на скорость v. mv — величина векторная, направленная так же, как скорость точки. Иногда К. д. называют ещё импульсом. При действии силы К. д. точки изменяется в общем случае и численно и по направлению; это изменение определяется вторым законом динамики. Q=mV – кол-во дв. мат. точки.

15) Элементарный импульс силы. Импульс силы за короткий промежуток времени.

Действие силы на материальную точку в течении времени можно охарактеризовать элементарным импульсом силы .

За конечный промежуток времени эта величина равна определённому интегралу от элемен­тарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время.