19)Частные случаи привидение пространственной системы сил к центру

Любая система сил, действующих на абсолютно твердое тело, может быть заменена одной силой R, равной главному вектору этой системы сил и приложенной к произвольно выбранному центру О, и одной парой сил с векторным моментом L_O, равным главному моменту системы сил относительно центра О.

Такая эквивалентная замена данной системы сил силой R и парой сил с моментом L_O называют приведением системы сил к центу О.

В результате приведения пространственной системы сил к произвольному центру О возможны следующие случаи, зависящие от векторов R и L_O:

1. если R = 0, L_O = 0, то заданная система является равновесной;

2. если хотя бы одна из величин R или L_O не равна нулю, то система сил не находится в равновесии.  При этом:

   • Eсли R = 0 и L_O 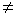  0, то система сил приводится к одной паре сил с моментом L_O. В этом случае величина момента L_O не зависит от выбора центра О.

   • Eсли R  0, L_O = 0, то система сил приводится к равнодействующей силе R^* = R, линия действия которой проходит через центр О.

   • Eсли R  0, L_O   0 и эти векторы взаимно перпендикулярны, то система сил также приводится к равнодействующей силе R^* = R, но линия ее действия не проходит через центр О. 

20)Центр тяжести твердого тела

Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела. 

Кинематика

1) Способы задания движения точки и уравнения движения

Векторный

Положение точки определяется радиус-вектором, проведенным из неподвижной точки, связанной с телом отсчета:       − векторное уравнение движения точки.

Координатный

В этом случае задаются координаты точки как функции времени:

Естественный для задания движения надо знать

Траекторию движения

Выбрать начало отсчета

Задать полож направление движения

Знать f изменения криволинейной координаты

S=S(t)

2) Скорость и ускорение точки при векторном способе задания движения

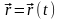
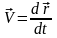
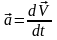Так же в зависимости от угла (а) зависит характер движения

а<90 ускорение, а>90 замедление, а=90 равномерное

3)Скорость и ускорение точки при координатном способе задания движения

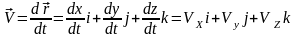
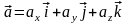
4)Скорость и ускорение точки при естественном способе задания движения

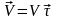
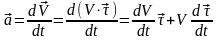
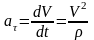
aτ=τ⋅dV/dt=τ⋅d2S/dt2, aτ=dV/dt=τ⋅d2S/dt2- касательное ускорение; оно характеризует быстроту изменения величины скорости точки;

an=n⋅V2/ρ, an=V2/ρ - нормальное ускорение точки; характеризует быстроту изменения направления вектора скорости;

ρ - радиус кривизны траектории в данной точке (для окружности:ρ=R , для прямой линии ρ=∞ ).

5)Поступательное движение твердого тела

Это движение, при котором любая прямая проведенная в теле, при его движении остается парралельным своему первоначальному положению.

При этом движении все его точки описывают одинаковые траектории и в каждый момент времени имеют равную скорость и ускорение.

6) Вращательное движение тела вокруг не подвижной оси уравнение вращательного движения

Это такое движение при котором 2-е точки данного тела неподвижны Уравнение

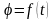
7) Угловая скорость и ускорение вращательного тела

Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.

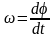
Угловым ускорением называют степень изменения угловой скорости.

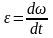
_{8) Скорость и ускорение точки тела при вращательном движении вокруг не подвижной оси}

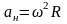
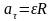
_{9) Выражение скорости и ускорения точки вращающегося тела в виде векторного произведения}

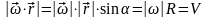
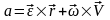
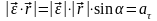
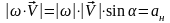
10) Плоскопараллельное движение. Уравнение движения плоской фигуры

Это такое движение, при котором все точки тела движутся в плоскостях параллельно неподвижной плоскость

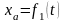
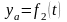
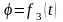
11) Теорема о скоростях точек плоской фигуры.

V любой точки плоской фигуры = геометр. сумме скорости полюса и скорости точки во вращении вокруг данного полюса

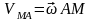
12) Теорема о проекциях скоростей двух точек плоской фигуры

Проекции скоростей 2-х точек плоской фигуры на ось проходящую через эти 2-е точки равны.

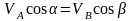
13) Мгновенный центр скоростей.

Это точка р плоской фигуры , V которой =0 в данный момент времени

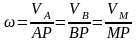
14) Определение скоростей точек и угловой скорости плоской фигуры с помощью мгновенного центра скоростей И 15) Способы определения положения мгновенного центра скоростей.

Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.

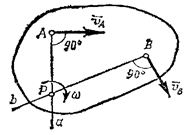
Легко убедиться, что если фигура движется не поступательно, то такая точка в каждый момент времени t существует и притом единственная. Пусть в момент времени t точки А и В плоской фигуры имеют скорости и , не параллельные друг другу (рис.33). Тогда точка Р, лежащая на пересечении перпендикуляров Аа к вектору и Вb к вектору , и будет мгновенным центром скоростей так как . В самом деле, если допустить, что , то по теореме о проекциях скоростей вектор должен быть одновременно перпендикулярен и АР (так как ) и ВР (так как ), что невозможно. Из той же теоремы видно, что никакая другая точка фигуры в этот момент времени не может иметь скорость, равную нулю.

Если теперь в момент времени взять точку Р за полюс, то скорость точки А будет так как . Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом

Из равенств, следует еще, что точек плоской фигуры пропорциональны их расстояниям от МЦС.

Полученные результаты приводят к следующим выводам.

1. Для определения мгновенного центра скоростей надо знать только направления скоростей и каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).

2. Для определения скорости любой точки плоской фигуры, надо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В. Тогда, восставив из точек А и В перпендикуляры к и , построим мгновенный центр скоростей Р и по направлению определим направление поворота фигуры. После этого, зная , найдем скорость любой точки М плоской фигуры. Направлен вектор перпендикулярно РМ в сторону поворота фигуры.

3. Угловая скорость плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от мгновенного центра скоростей Р: .

Рассмотрим некоторые частные случаи определения мгновенного центра скоростей.

а) Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого неподвижного, то точка Р катящегося тела, касающаяся неподвижной поверхности (рис.34), имеет в данный момент времени вследствие отсутствия скольжения скорость, равную нулю ( ), и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу.

б) Если скорости точек А и В плоской фигуры параллельны друг другу, причем линия АВ не перпендикулярна (рис.35,а), то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны . При этом из теоремы о проекциях скоростей следует, что т. е. ; аналогичный результат получается для всех других точек. Следовательно, в рассматриваемом случае скорости всех точек фигуры в данный момент времени равны друг другу и по модулю, и по направлению, т.е. фигура имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют еще мгновенно поступательным). Угловая скорость тела в этот момент времени, как видно равна нулю.

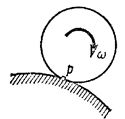рис 34 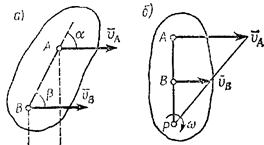рис 35

в) Если скорости точек А и В плоской фигуры параллельны друг другу и при этом линия АВ перпендикулярна , то мгновенный центр скоростей Р определяется построением, показанным на рис. 35,б. Справедливость построений следует из пропорции. В этом случае, в отличие от предыдущих, для нахождения центра Р надо кроме направлений знать еще и модули скоростей .

г) Если известны вектор скорости какой-нибудь точки В фигуры и ее угловая скорость , то положение мгновенного центра скоростей Р, лежащего на перпендикулярно к (рис.35,б), можно найти как .

16) Теорема об ускорениях точек плоской фигуры.

Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.

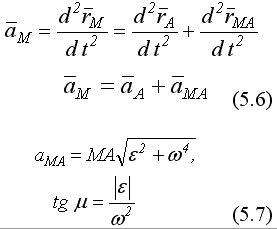
17) Абсолютное, относительное и переносное движение точки.

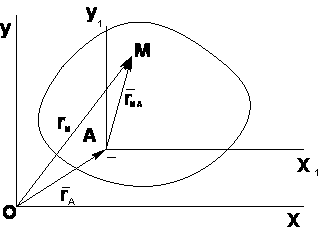
Движение точки по отношению к подвижной системы координат называется относительным.

Движение тела вместе с точкой М по отношению к неподвижной системе называется переносным (Vе)

Движение точки М по отношению к неподвижной системе называется абсолютным движением (Va)

18) Теорема о сложении скоростей точки при ее составном движении.

Утверждает, что при сложном движении материальной точки её абсолютная скорость равна сумме относительной и переносной скоростей.

19)Теорема Кориолиса о сложении ускорений точек

Абсолютное ускорение в сложном движении = геометрической сумме переносного, относительного движения и ускорения Кориолиса.

20) Модуль и направление ускорения Кориолиса. Случаи отсутствия ускорения Кориолиса при сложном движении.

Сначала определяем направление относительной скорости затем строим угловую скорость.

Вектор относительной скорости спроецируем на плоскость перпендикулярную угловой скорости и поворачиваем на 90 градусов проекцию в сторону поворота угловой скорости -это и будет ускорение Кориолиса

Когда ускорение Кориолиса =0

1) угловая скорость =0 в случае когда переностное движение является поступательным

2)относительная скорость =0 в точках остановки относительного движения

3) sinα = 0 когда векторы колиниарны ( отн и перен скоростей)