Кинематическое исследование плоских рычажных механизмов

Задачи: 1) определение положений звеньев и траекторий заданных точек;

2) определение линейных и угловых скоростей и ускорений звеньев и отдельных точек механизмов.

Кинематические исследования выполняютграфические методы (отн. простота, не очень точно)

аналитические методы (сложнее, точно, формулы пригодны для исследования динамики; ЭВМ).

Кинематические исследования начинают с ведущего звена и непосредственно к нему присоединяют группы Асура, затем переходят к остальным.

Графический метод: строят 12 или 24 положения в масштабе. Определяют скорости и ускорения звеньев.

П

1

2

3

4

1

2

3

4

5

6

7

8

9

10

11

12

лан механизма– масштабное графическое изображение кинематической схемы механизма, соответствующее заданному положению ведущего звена.

C

D

D

- определяет положение коромыслаCD

- функция положения

;Функции, не зависящие от абсолютных значений

;скоростей звеньев ; передаточные функции

1

2

3

4

5

6

7

8

9

10

11

12

k

1

2

3

4

5

6

7

8

9

10

11

12

h₁

(произвольно)

1

2

3

4

5

6

7

8

9

10

11

12

h₂

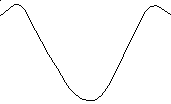
Определение скоростей и ускорений

Принимают ;(ведущего звена)

Тогда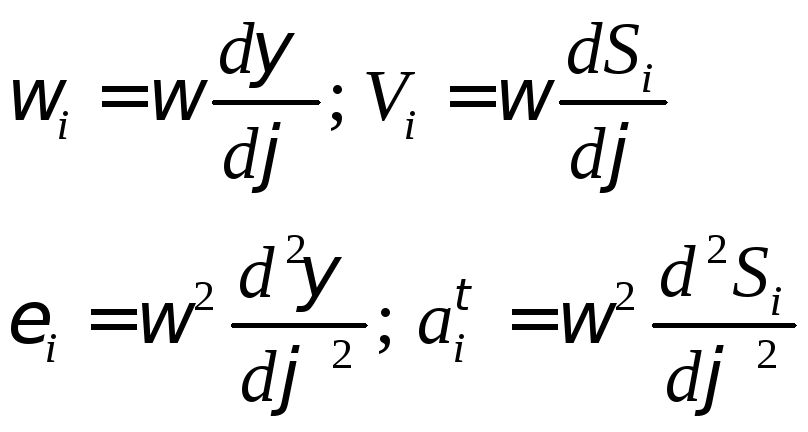

- безразмерные передаточные функции 1го и 2го порядков.

«аналогии» скоростей и ускорений.

План скоростей

Предложен O.Mohrв 1870 г. Основана на методах ТМ.

А

B

C

E

D

S

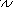
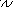
P-полюс

Если отрезок схемы механизма, то коэффициентназывается «масштабом кривошипа».

b

E

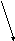
|| EG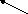

P,a,d

S

E

P,f₆

f₅

g

c

Теорема подобия скоростей:

Отрезки прямых линий, соединяющих точки на схеме звена, механизма, и отрезки прямых линий, соединяющих концы векторов относительных скоростей этих точек на плане скоростей, образуют подобные и сходственно расположенные фигуры. Фигура на плане скоростей повернута относительно фигуры схемы звена на 90^о.

Аналитический метод (теор. мех.)

Лекция № 3

План ускорений.

Из теории машин: , где

Если

Выбираем полюс и величину отрезка,. Определяем масштабный коэффициент:

p.s. Еслисхемы механизма, то коэффициентназывается «масштабом крипошива»

C

D

B

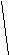
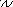
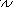
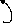
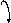
E

G

A

D

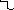
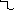
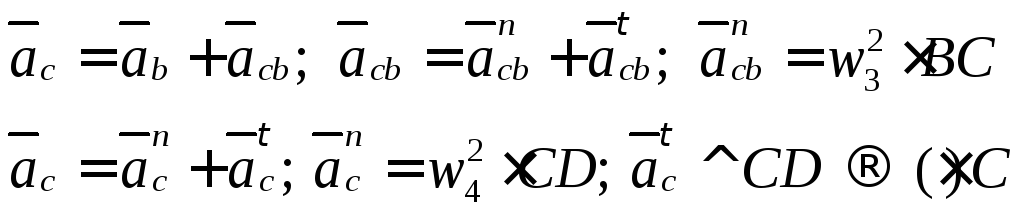
Теорема подобия для ускорений

Отрезки прямых линий, соединяющие данные точки на плане звено, и отрезки прямых, соединяющие концы векторов полных ускорений этих точек на плане ускорений, образуют подобные и сходственно расположенные фигуры.

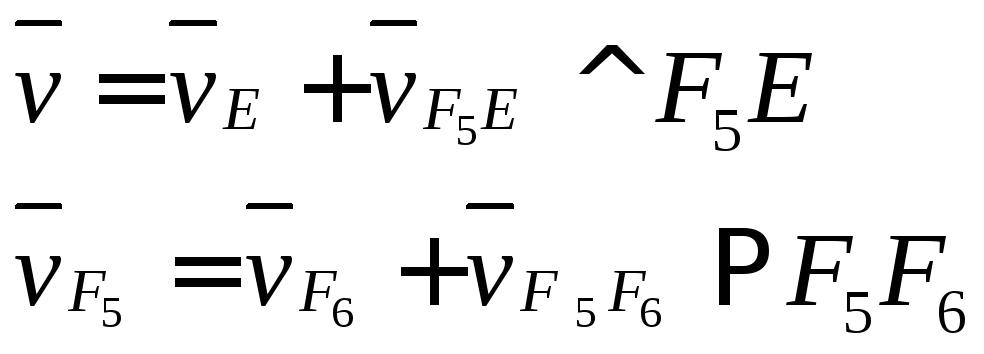
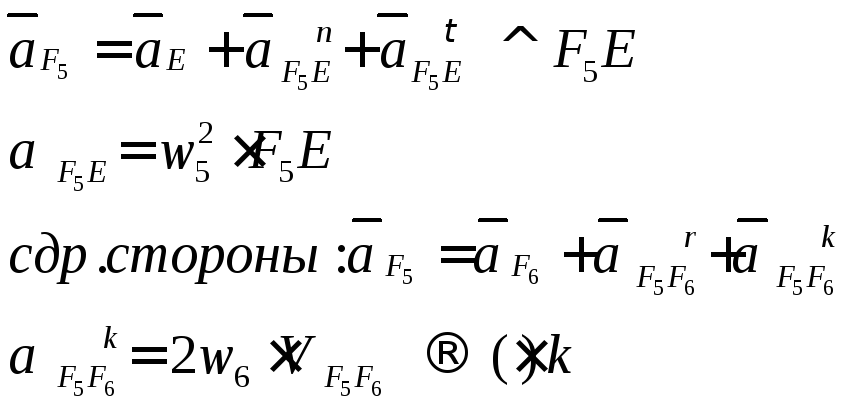
Кулисный механизм.

B₁;B₂;B₃

A

C

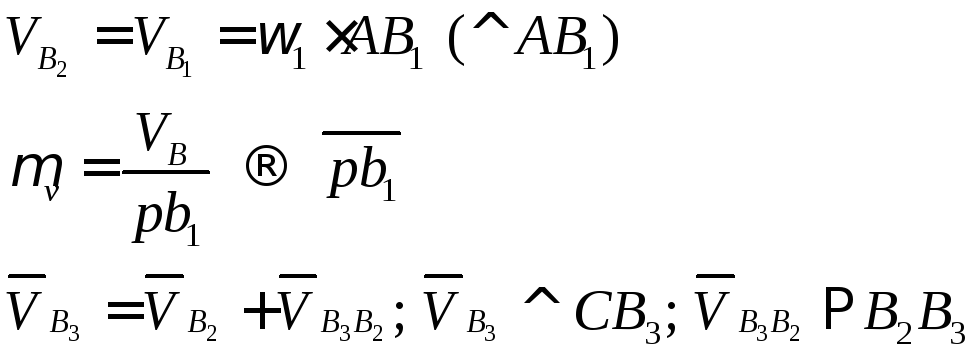
План скоростей.

P,a,c

b₃

b₁, b₂

d

П

лан ускорений

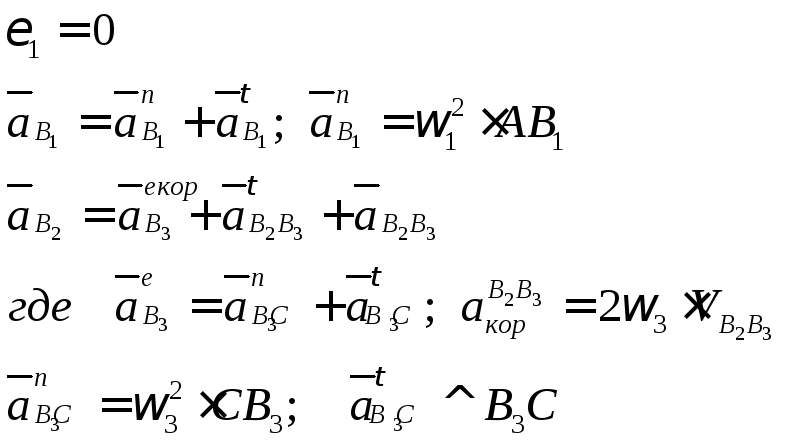
Свойство полюса. Полюс плана ускорений является отражением всех точек механизма, ускорение которых в данном положении равно нулю.

Лекция №4