Силы, действующие на зубья колес

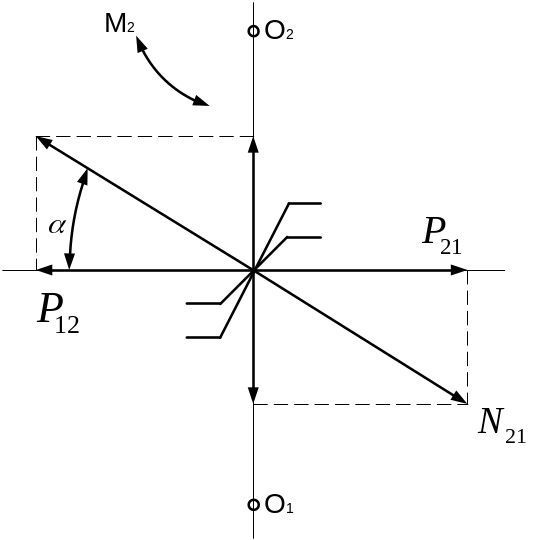
Если не учитывать силы трения, то действующие на зубья силы N будут направлены по общей нормали к профилям зубьев колес 1 и 2 в зоне их контакта. Нормальные силы N можно разложить на составляющие: окружные P и радиальные Q. Величина этих сил зависит от приложенного к валу момента µ2. зависимость между этими силами:

Эти силы учитывают при расчете зубьев колес, валов и подшипников механизма.

Наибольшие нормальные силы действуют на зубья колес, когда в зацеплении находится одна пара зубьев, при этом зона их контакта находится около полюса зацепления. Поэтому усталостное разрушение зубьев происходит в средней части боковой поверхности зуба. Неточности изготовления и сборки передачи, упругие деформации валов и колес, толчки и удары, происходящие в момент входа зубьев в зацепление, учитывают путем введения в расчетные формулы коэффициента концентрации нагрузки Кк и коэффициента динамичности нагрузки Кд.

Расчетную удельную нагрузку q (Н/м)при длине полоски контакта зубьев B определяют по формуле:

q=N*Kk*Kд/B.

Коэффициент концентрации нагрузки определяется отношением наибольшей удельной нагрузки к ее средней величине Кк=qmax/q. Принимают Кк=1 при расположении колес посередине между подшипниками, при коротких и жестких валах и при колесах, изготовленных из пластмасс, бронзы или стали, если твердость поверхности зубьев НВ<350, так как упругая податливость и быстрая приработка зубьев уменьшают неравномерность распределения нагрузки по длине зуба. Ориентированные значения Кк=1,1…1,3. При этом Кк соответственно увеличиваются с увеличением =В/А от 0,4 до 1. Кк тем больше, чем меньше жесткость валов, тверже материал зубьев (НВ>350), ниже степень точности колес относительно подшипников.

Коэффициент динамичности нагрузки определяется отношением полной нагрузки к нормальной силе Кд=(N+Nд)/N. Величина динамической нагрузки Nд тем больше, чем ниже степень точности колес, выше окружная скорость зубьев и больше массы звеньев, связанных с валами передачи.

Расчет зубьев на контактную прочность

Опытами установлено, что усталостное разрушение поверхности зубьев происходит в средней по высоте зуба зоне. Целью расчета является определение размеров колес, при которых расчетные контактные напряжения в материале зубьев не превышающей допустимой величины к.

В качестве теоретической основы расчета зубьев используется формула Герца, выражающая результаты исследования напряжений (МПа) в зоне контакта примятых друг к другу по образующим двух стальных цилиндров, где q – удельная нагрузка на 1 мм длины полоски контакта цилиндров, Н/м; En – приведенный модуль упругости материалов цилиндров, МПа; - приведенный радиус кривизны цилиндров, мм.

Выразим q и через параметры зубчатой передачи:

А=r2±r1=r1(i12±1); r1=A(i12±1); r2=Ai12(i12±1)

Где r1=0,5d1 и r2=0,5d2. Знак плюс относится к передачам внешнего зацепления, а знак минус – внутреннего зацепления. Радиусы кривизны эвольвент при контакте зубьев в полюсе зацепления:

Приведенный модуль упругости при разных материалах зубьев значения E1 и Е2 – из таблиц.

Нормальная сила

Расчетная удельная нагрузка на зуб

Подставляя приведенные значения q En и , получим формулу для определения константного напряжения снятия

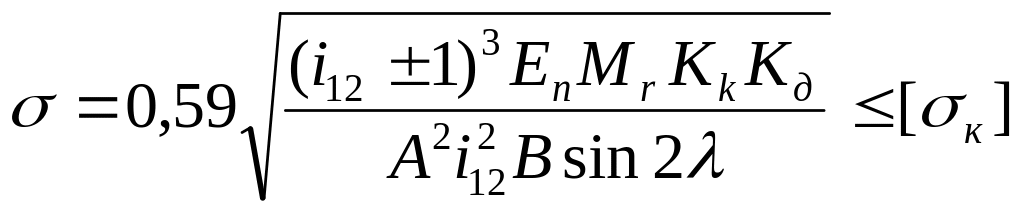
Задаваясь отношением и значением [ ]к, можно определить расчетное межосевое расстояние.