
- •Классификация электрических цепей
- •Вопрос 1. Что называется электрическим током, напряжением, энергией и мощностью?
- •Вопрос 2. Что называется электрической цепью? Виды эц.
- •Вопрос 3. Активные и пассивные компоненты электрической цепи
- •(Только обозначение не I, а j)
- •Замещение физических устройств идеализированными элементами электрической цепи
- •Вопрос 4. Электрическая схема. Топология электрической цепи
- •Вопрос 5. Законы Ома и Кирхгофа для электрической цепи
- •П ервый закон Кирхгофа
- •Вопрос 6. Принцип эквивалентности. Преобразование эс
- •Вопрос 7. Принцип наложения. Теорема замещения. Теорема взаимности
- •Вопрос 8. Теорема об активном двухполюснике. Теорема Тевенина и Нортона
- •Вопрос 9. Принцип дуальности. Теорема Телледжена. Баланс мощности
- •Вопрос 10. Режимы работы
- •Вопрос 11. Анализ электрических цепей
- •Вопрос 12. Суть метода суперпозиции при анализе электрической цепи и есть ли ограничения на его использование
- •Вопрос 13. Матричное представление методов контурных токов и узловых потенциалов
Замещение физических устройств идеализированными элементами электрической цепи
Рассмотренные идеализированные резистивный, индуктивный и емкостной элементы могут служить простейшими моделями реальных физических устройств. К реальным физическим устройствам можно отнести: резистор, катушку индуктивности, конденсатор.
При постоянном и переменном токе в области нижних частот резистор можно рассматривать как идеализированный резистивный элемент, т.е.

Рассмотрим,
как можно представить конденсатор,
состоящий из двух параллельных пластин,
разделенных диэлектриком. При постоянном
напряжении и идеальном диэлектрике
конденсатор пропускать ток не будет
(разрыв в цепи). При переменном напряжении
в области нижних частот модель
конденсатора, кроме емкостного элемента,
может содержать параллельную проводимость
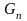 ,
учитывающую потери энергии в диэлектрике.
,
учитывающую потери энергии в диэлектрике.
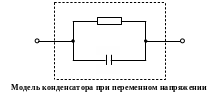
Теперь
представим себе простейшую катушку
индуктивности в виде нескольких круговых
витков проводника, по которому проходит
ток. При постоянном токе катушка
индуктивности может быть представлена
как сопротивление
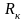 ,
которое учитывает сопротивление витков
проводника. При переменном токе в области
нижних частот катушка индуктивности
может быть представлена как индуктивность
с последовательно включенным сопротивлением
.
,
которое учитывает сопротивление витков
проводника. При переменном токе в области
нижних частот катушка индуктивности
может быть представлена как индуктивность
с последовательно включенным сопротивлением
.

В области более высоких частот модели резисторов, катушек индуктивности и конденсаторов становятся более сложными. Например, на сверхвысоких частотах (СВЧ) в резисторе начинает проявляться поверхностный эффект, выражающийся в неравномерном распределении тока по сечению проводника (скин-эффект). В результате этого сопротивление проводника начинает расти с увеличением частоты.
Вопрос 4. Электрическая схема. Топология электрической цепи
Электрической схемой называют графическое изображение электрической цепи. Микросхемой (интегральной схемой) называют интегральную электрическую цепь, содержащую сотни и тысячи простейших активных и пассивных элементов.
 Для
анализа электрических цепей в последнее
время применяют топологические методы,
заключающиеся в представлении
электрической цепи в виде графа. Граф
– геометрическая система линий (ветвей),
соединяющих заданные точки (узлы). Граф,
у которого ветви ориентированы по
направлению токов ветвей, является
направленным (ориентированным). Пусть
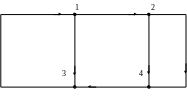
дана электрическая схема в виде:
Для
анализа электрических цепей в последнее
время применяют топологические методы,
заключающиеся в представлении
электрической цепи в виде графа. Граф
– геометрическая система линий (ветвей),
соединяющих заданные точки (узлы). Граф,
у которого ветви ориентированы по
направлению токов ветвей, является
направленным (ориентированным). Пусть
дана электрическая схема в виде:

Основные понятия и определения в топологии цепей:
Узел – место соединения зажимов трех и более элементов.
Ветвь – часть цепи, включаемой между двумя узлами, через которые она обменивается энергией с остальной цепью. Ветви, присоединённые к одной паре узлов, образуют параллельное соединение.
Путь – последовательно соединенные ветви цепи.
Контур – любой замкнутый путь, проходящий по нескольким ветвям.
Ветви считаются соединенными последовательно, если они обтекаются одним и тем же током. Ветви считаются соединенными параллельно, если они присоединены к одной и той же паре узлов. Таким образом, при последовательном соединении элементов общим параметром для них является ток, при параллельном – напряжение между узлами
Цепь,
в которой отсутствуют разветвления,
называют одноконтурной, при наличии
разветвлений – многоконтурной.
Многоконтурная цепь характеризуется
числом независимых контуров. Совокупность
независимых контуров определяется тем,
что каждый из последующих контуров,
начиная от элементарного, отличается
по меньшей мере одной новой ветвью.
Число независимых контуров может быть
определено по формуле Эйлера:
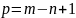 ,
где m – количество ветвей, n – количество
узлов, причем m > n всегда.
,
где m – количество ветвей, n – количество
узлов, причем m > n всегда.
Например. Проведём топологический анализ следующей схемы:

