Шпаргалка По Физике К Экзамену Для Дневников (Дроздов С. А.)_2 / шпоры / 28 Циркуляция вектора магнитной индукции

Циркуляция вектора магнитной индукции для магнитного поля в вакууме. Теорема о циркуляции вектора магнитной индукции. Магнитное поле соленоида.

Циркуляцией вектора В по заданному замкнутому контуру называется интеграл:

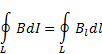
Теорема о циркуляции вектора В магнитной индукции:

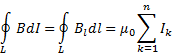
Магнитное поле соленоида:

Магнитное поле внутри соленоида является однородным, и неоднородным вне соленоида. Чем длиннее соленоид, тем меньше магнитная индукция вне его.

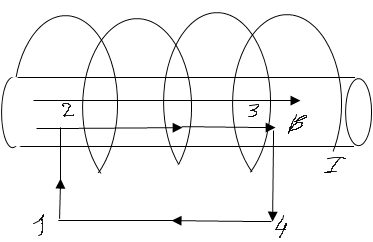
найдем цирку­ляцию вектора В по прямоугольному контуру 1234, показанному на рис.∫₁₂Bdl=∫₃₄Bdl=0 (угол между В и dlпо этим участкам равен π/2). ∫₁₂₃₄₁Bdl=∫₂₃Bdl= = В L = μ₀ ∑ I = μ₀ n L I , В L = μ₀ n L I, Тогда величина магнитной индукции определится как произведение В = μ₀ n I,где n = N/L– число витков на единицу длины соленоида, nI - называют числом ампер-витков. Магнитная индукция В направлена по оси соленоида. Полученная формула справедлива для средней части соленоида, длина которого L много больше, чем его диаметр. Если это не так, то величина индукции магнитного поля соленоида в произвольной точке А, лежащей на оси соленоида : В = ,где α₁ , α₂ - углы, под которыми из точки А видны концы соленоида.