5.1. Пример Расчёта методом двух узлов

5.1.1. Задаем произвольно направления токов в ветвях исходной схемы.

5.1.2. Преобразуем пассивный треугольник сопротивлений в эквивалентную звезду сопротивлений.

Рассмотрим схему на рис. 5.1.

Рис. 5.1

В данной схеме (рис. 5.1) пассивным является треугольник, содержащий сопротивления R₄, R₅, R₆.

Упрощаем схему путём преобразования пассивного треугольника в эквивалентную звезду (рис. 5.2).

2

R₄₆

R_{56 01} R₄₅

3 1

Рис. 5.2

5.1.3. В результате преобразования получим схему с двумя узлами (рис. 5.3).

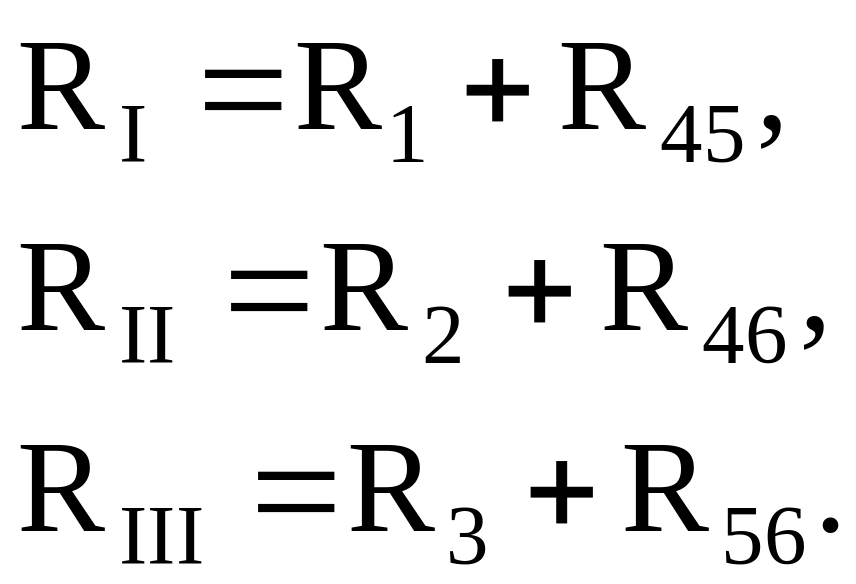
a б

Рис. 5.3

5.1.4. Задаем направление токов и напряжение в ветвях преобразованной схемы.

5.1.5. Для схемы рис. 5.4 определяем проводимость ветвей:

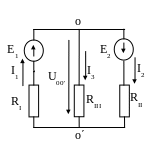
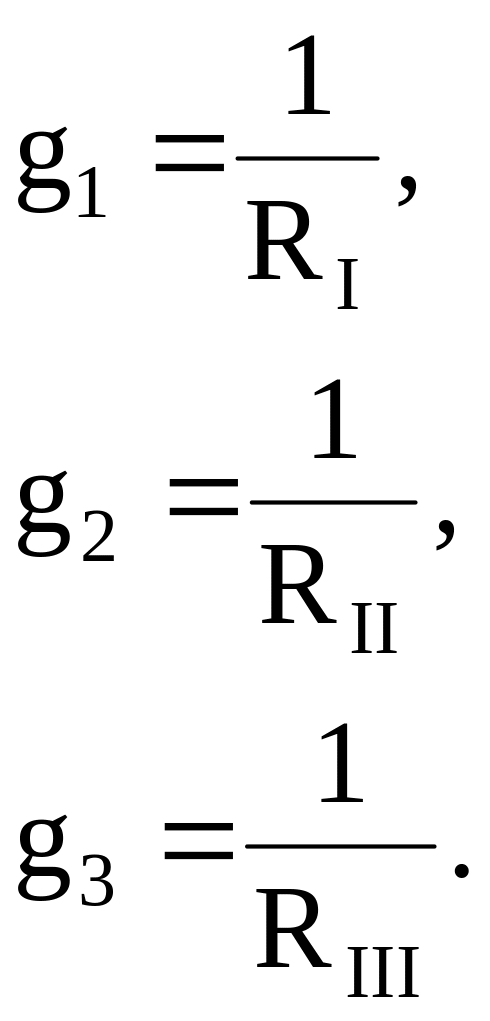
Рис. 5.4

5.1.6. Определяем узловое напряжение, используя метод двух узлов.

Для схемы рис. 5.4

где знак () зависит от взаимного направления ЭДС и узлового напряжения (знак (+), если они направлены встречно).

5.1.7. Определяем токи в ветвях упрощенной схемы по закону Ома для активного участка цепи:

где знак (+) ставится в том случае, если направление тока совпадает с направлением или .

Для схемы рис. 5.4

5.1.8. Находим остальные токи в исходной не преобразованной схеме с помощью уравнений второго закона Кирхгофа.

Для схемы рис. 5.5 уравнения второго закона Кирхгофа имеют вид (направление обхода контуров – по часовой стрелке):

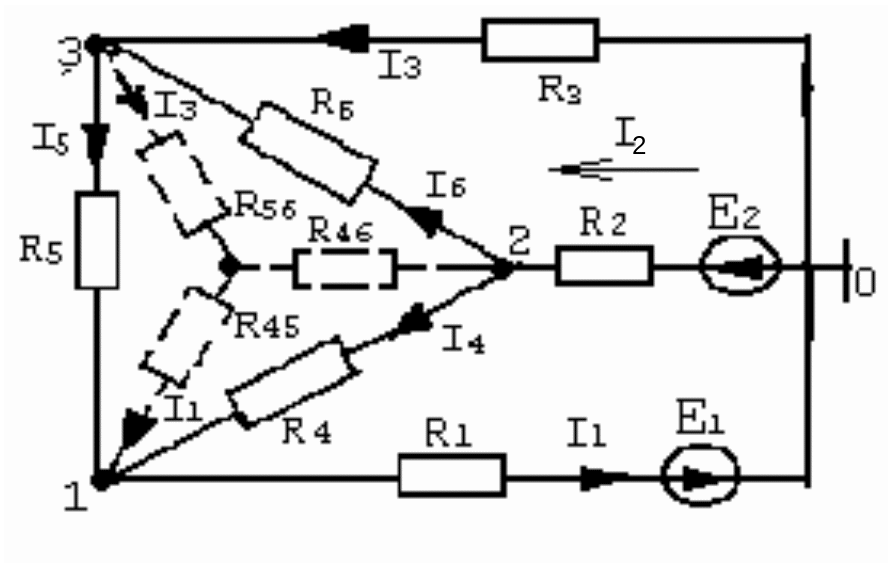
Рис. 5.5

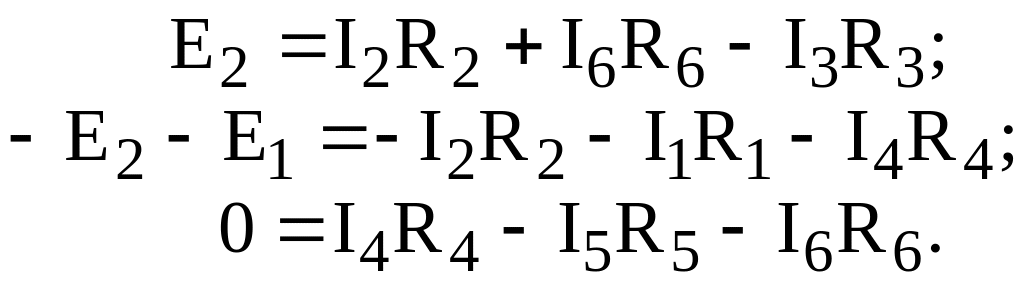
Отсюда получаем:

Если в результате решения этих уравнений ток получится со знаком (−), то это означает, что действительное направление тока противоположно выбранному.

5.1.9. Делаем проверку расчётов по первому закону Кирхгофа для любых двух узлов, используя исходную схему и расчётные значения токов.

5.2. Пример Расчёта методом контурных токов

5.2.1. Выбираем направление контурных токов и положительные направления токов во всех ветвях (рис. 5.6).

Рис. 5.6

5.2.2. Составляем систему двух уравнений:

где R₁₂ = R₂₁ − взаимные сопротивления контуров; R₁₁, R₂₂ − собственные сопротивления контуров, равные сумме сопротивлений соответствующего контура; E₁₁, E₂₂ − алгебраическая сумма ЭДС соответствующего контура.

Знак взаимного сопротивления определяется направлением контурных токов в нем. Если контурные токи во взаимном сопротивлении совпадают по направлению, то R₁₂ берется со знаком (+), если нет, то со знаком (−).

Для схемы рис. 5.6 уравнения имеют вид:

Если направление ЭДС совпадает с направлением контурного тока, ставится знак (+), если не совпадает, то знак (−).

5.2.3. Решаем полученную систему уравнений с помощью определителей:

.

Токи во внешних ветвях равны соответствующим контурным токам, а в смежных  алгебраической сумме соответствующих контурных токов.

.

Для схемы рис. 1.6 , т.к. контурные токи в резисторе R_III направлены навстречу друг другу.

5.2.4. Делаем проверку по первому закону Кирхгофа и сравниваем значения токов с результатами других методов расчёта.

5.3. Пример определения ТОКА I_k (k = 5)