II. Расчёт баланса мощностей
Баланс мощностей для электрической цепи является математическим подтверждением закона сохранения энергии и в данном задании является основной проверкой правильности проведенных вычислений.
Уравнение баланса мощностей:
.
Знак «+» в левой части равенства берётся, когда ЭДС и ток в схеме совпадают по направлению. Ошибка баланса не должна превышать ±2 %, относительно суммарной мощности источников питания.
III. Построение потенциальной диаграммы
Потенциальная диаграмма позволяет проследить за изменением потенциала между характерными точками какого-либо контура схемы и является одним из методов проверки расчётов. Для построения потенциальной диаграммы рекомендуется выбрать контур исходной схемы, имеющий два источника ЭДС.
а) В ветвях контура задаем направления полученных токов и произвольное направление обхода контура.
б) Одну из точек контура заземляем и относительно неё вычисляем потенциалы других точек. Например, для приведенного на рис.3 контура, расчет будет таким:
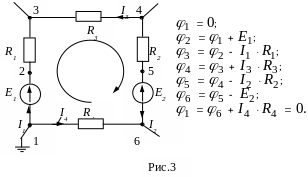
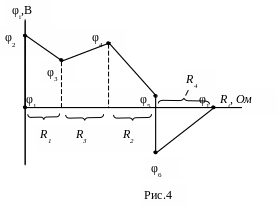
в) Выбираем масштаб и строим потенциальную диаграмму i(Ri). Согласно ранее проведенным расчетам она может иметь вид, например, как на рис. 4.
Задание № 2 расчёт однофазных цепей переменного тока
Цель задания – приобретение навыков анализа и расчета цепей переменного тока.
В ходе выполнения задания требуется:
рассчитать токи во всех ветвях и напряжениях на всех участках и элементах схемы;
рассчитать баланс мощностей;
построить векторную диаграмму токов и напряжений.
Частота напряжения питания для всех вариантов =50 Гц. Начальная фаза напряжения источника питания u=0. Точность вычислений – два знака после запятой.
Исходные данные для расчета приведены в приложении 2.
I. Алгоритм расчета символическим методом
а) Находим величины реактивных сопротивлений:
,
Ом;
,
Ом,
где L
– индуктивность, задана в
,
т.е.
Гн; C
– ёмкость, задана в
,
т.е.
Ф;
и
допускается округлять до целого числа.
б) Определяем полные комплексные сопротивления каждой ветви в алгебраической и показательной форме, например:
,
Ом,
где
– модуль комплекса полного сопротивления
первой ветви;
– угол сдвига по фазе между напряжением
и током первой ветви.
Знак «+» соответствует индуктивному характеру сопротивления, знак «–» – ёмкостному.
в) Составляем схему замещения и обозначаем на ней токи и напряжения каждой ветви, например, как на рис. 5. При расчетах оперируем числами в комплексной форме.
г) Находим эквивалентное сопротивление всей цепи:
,
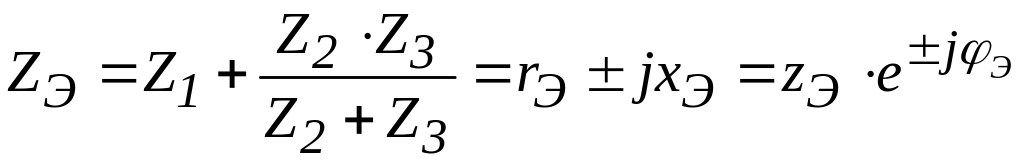где
и
– эквивалентные активное и реактивное
сопротивления всей цепи;
– модуль активного сопротивления;
– угол сдвига по фазе между напряжением
и током всей цепи.
При нахождении эквивалентного сопротивления сложение ведется в алгебраической форме представления комплексного числа, умножение и деление – в показательной.
д) Рассчитываем токи в ветвях:
;
;
.
е) Рассчитываем напряжения ветвей:
;
.
Найденные значения токов и напряжений должны быть представлены в алгебраической и показательной формах. Расчет допускается вести другими способами.
ж) Проверяем правильность вычислений по законам Кирхгофа:
;
.
з) Рассчитываем напряжения на активных, ёмкостных и индуктивных элементах, например:
;
;
и т.д.