§ 3.3 Примеры частных задач синтеза оптимальной структуры ас

Пример 1. [1] . Сначала решим методом "ветвей и границ" следую­щую задачу: найти минимум

(3.3.1)

при

,	(3.3.2)
,	(3.3.3)
,	(3.3.4)
	(3.3.5)

Условие (3.3.2) означает, что каждый узел может решать только одну задачу. Условие (3.3.3) означает, что каждая задача может решаться только в одном узле.

Будем изображать множество вариантов кружками, в верхней части которых проставлен номер множества, а в нижней - значение нижней границы (рис. 3.3.1).

Рис. 3.3.1. Процедура ветвления

Для вычисления нижней границы используется соотношение

(3.3.6)

где

i* ‑ число рассмотренных уровней ветвления.

Для исходного множества (обозначим его через "0") соотношение (3.3.6) имеет вид , т.е. из матрицы (3.3.5) выбираются минимальные числа, причем условие (3.3.2) мо­жет нарушаться. Итак,

Вершины первого уровня получим,  поочередно закрепляя пер­вую задачу за первым,  вторым, третьим и четвертым узлами. Со­ответствующие значения нижней границы представлены в табл. 3.3.1.

вершины второго уровня получим, закрепив первую задачу за четвертым узлом. Соответствующие значения нижней границы пред­ставлены в таблице 3.3.2.

Из таблицы 3.3.2 следует,  что вторую задачу следует закре­пить за третьим узлом.

Вершины третьего уровня получим, закрепив первую задачу за четвертым узлом и вторую за третьим. Соответствующие значе­ния нижней границы представлены в табл. 3.3.3.

 

Таблица 3.3.1 Таблица 3.3.2 Таблица 3.3.3

Из табл. 3.3.3 следует, что задача 3 должна быть за­креплена за узлом один. Чет­вертая задача однозначно за­крепляется за узлом 2.

Окончательный ответ представлен в матрице

Значение целевой функции равно 10.

Пример 2.

Рассмотрим решение первой частной задачи синте­за оптимальной структуры. Найти

при ограничениях

 

В соответствии с ранее рассмотренным алгоритмом произво­дим упрощение матрицы , для чего исключаем элементы, для которых выполняется условие а_ij > b_j. Первая строчка после исключе­ния на содержит ни одного элемента, т.е. первая задача не мо­жет быть решена: решение отсутствует.

Пусть b_j = |3 6 5 2|. Тогда после исключения имеет вид

Первая строчка содержит только один элемент а₁₂ = 5, сле­довательно, он обязательно войдет в решение. В отличие от рас­смотренного ранее примера, мы сняли условие, согласно которому один узел может быть загружен только одной задачей. Ресурс на второй узел равен 6, следовательно, остается резерв: 6 ‑ 5 = 1,

Далее процедура аналогична рассмотренной выше, но каждый раз ищутся минимальные элементы в столбцах и проверяется, не нагружен ли данный узел.

Итак, x₁₂ = 1. Имеем

Выбираем минимальные элементы в каждой строке. Загрузка не превышает заданную. Окончательно

Значение целевой функции в первом случае 5 + 2 + 1 + 2 = 10, во втором 5 + 2 + 1 + 2 = 10. Варианты равнозначны.

Пример 3.

Рассмотрим числовое решение задачи минимизации общих затрат при ограничениях на общее время решения, т.е. бу­дем искать

(3.3.7)

При

	(3.3.8)
	(3.3.9)
	(3.3.10)

Пусть

Сначала находим минимальные элементы в каждой строке мат­рицы и  проверяем, удовлетворяется ли условие (3.3.8) по одноименным элементам матрицы:

Условие (3.3.8) не выполняется и задачу "в лоб" решить не удается. Приступим к упрощению матрицы. Для матрицы по­следовательно для всех элементов проверяется условие

(3.3.11)

где - рассматриваемый элемент;

b_lj - минимальные элементы строк;

Элемент   b₁₄   не удовлетворяет условию (3.3.11), он исклю­чается из матрицы , и одноименный элемента₁₄ исключа­ется из матрицы . Аналогично:

Из матрицы выбираем минимальные элементы и подсчи­тываем время решения: 2 + 5 + 3 + 4 + 5 = 19 < 20. Задача реше­на. Если бы это не удалось, пришлось бы вести ветвление и каж­дый минимальный вариант проверять на условие (3.3.8). Итак, ответ:

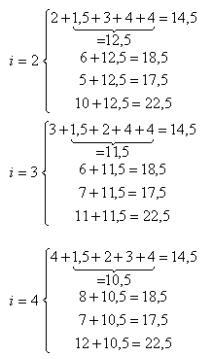
[1] Пример имеет цель продемонстрировать процедуру ветвления.