1. Волны. Распространение волн, уравнение плоской и сферической волн, фазовая скорость, волновое уравнениe.

Волна́ — изменение некоторой совокупности физических величин (характеристик некоторого физического поля или материальной среды), которое способно перемещаться, удаляясь от места его возникновения, или колебаться внутри ограниченных областей пространства. Уравнением волны  называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t. Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны. Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:   . Пусть колебание точек, лежащих в плоскости x=0 , имеет вид     Следовательно, колебания частиц в плоскости x будут отставать по времени на t  от колебаний частиц в плоскости  , т.е.  это уравнение плоской волны.Таким образом, x  есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания постоянна . Это будет, если энергия волны не поглощается средой. Уравнение сферической волны.В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt. Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу   . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону 1/r . Следовательно, уравнение сферической волны: . Уравнение неприменимо для малых r, т.к. при r->0 , амплитуда стремится к бесконечности. Скорость распространения синусоидальной волны n называется фазовой скоростью; это есть скорость распространения фиксированной фазы волны. Для простой синусоидальной волны фиксированная фаза соответствует фиксированной амплитуде.   Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым. Найдем общий вид волнового уравнения. Для этого продифференцируем дважды уравнение плоской волны по времени t и всем координатам:

2 . Действие магнитного поля на токи и заряды. Проводник в магнитном поле, взаимодействие 2-х проводников с током . Движение заряженной частицы в однородном постоянном магнитном поле.

3. Диэлектрики в электрическом поле. Молекулярная картина поляризации диэлектрика, величины, характеризующие поляризацию диэлектрика

В диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика. При внесении диэлектрика во внешнее электрическое поле      в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов. Связанные заряды создают электрическое поле   которое внутри диэлектрика направлено противоположно вектору напряженности   внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле    внутри диэлектрика оказывается по модулю меньше внешнего поля  . Физическая величина, равная отношению модуля напряженности   внешнего электрического поля в вакууме к модулю напряженности   полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества.  ; Существует несколько механизмов поляризации диэлектриков. Основными из них являются ориентационная и электронная поляризации. Ориентационная или дипольная поляризация возникает в случае полярных диэлектриков, состоящих из молекул, у которых центры распределения положительных и отрицательных зарядов не совпадают. Такие молекулы представляют собой микроскопические электрические диполи – нейтральную совокупность двух зарядов, равных по модулю и противоположных по знаку, расположенных на некотором расстоянии друг от друга. Дипольным моментом обладает, например, молекула воды, а также молекулы ряда других диэлектриков (H₂S, NO₂ и т. д.). Поляризация полярных диэлектриков сильно зависит от температуры, так как тепловое движение молекул играет роль дезориентирующего фактора. Электронный или упругий механизм проявляется при поляризации неполярных диэлектриков, молекулы которых не обладают в отсутствие внешнего поля дипольным моментом. Под действием электрического поля молекулы неполярных диэлектриков деформируются – положительные заряды смещаются в направлении вектора    а отрицательные – в противоположном направлении. В результате каждая молекула превращается в электрический диполь, ось которого направлена вдоль внешнего поля. На поверхности диэлектрика появляются нескомпенсированные связанные заряды, создающие свое поле    направленное навстречу внешнему полю   Так происходит поляризация неполярного диэлектрика. Электрическое поле     связанных зарядов, возникающее при поляризации полярных и неполярных диэлектриков, изменяется по модулю прямо пропорционально модулю внешнего поля   В очень сильных электрических полях эта закономерность может нарушаться, и тогда проявляются различные нелинейные эффекты. В случае полярных диэлектриков в сильных полях может наблюдаться эффект насыщения, когда все молекулярные диполи выстраиваются вдоль силовых линий. В случае неполярных диэлектриков сильное внешнее поле, сравнимое по модулю с внутриатомным полем, может существенно деформировать атомы или молекулы вещества и изменить их электрические свойства. У многих неполярных молекул при поляризации деформируются электронные оболочки, поэтому этот механизм получил название электронной поляризации. Если в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд Q, то напряженность поля   создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме: ;

4 .Магнитное поле токов в вакууме. Понятие магнитного поля, закон Био - Савара – Лапласа. Понятие магнитного поля. Магнитное поле – это силовое поле, действующее на движущиеся заряды, токи и на тела, обладающие магнитным моментом (магнитные диполи). Магнитное поле создаётся движущимися зарядами, электрическими токами, магнитными моментами (диполями). Постоянные токи, неподвижные магнитные диполи создают постоянные магнитные поля. Магнитное поле характеризуется вектором магнитной индукции B..Принцип суперпозиции магнитных полей. Опыт дает, что для магнитного поля, как и для электрического, справедлив принцип суперпозиции: поле , порождаемое несколькими движущимися зарядами (токами) равно векторной сумме полей порождаемых каждым зарядом (током) в отдельности: ;

магнитная индукция поля прямого тока магнитная индукция поля в центре кругового проводника с током

5-6) Магнитный диполь— аналог электрического, который можно представить себе как систему двух «магнитных зарядов» (эта аналогия условна, так как магнитных зарядов, с точки зрения современнойэлектродинамики, не существует). В качестве модели магнитного диполя можно рассматривать небольшую (по сравнению с расстояниями, на которых изучается генерируемое диполеммагнитное поле) плоскую замкнутую проводящую рамку площади по которой течёт ток При этом магнитным моментом диполя (в системеСГСМ) называют величину где — единичный вектор, направленный перпендикулярно плоскости рамки в том направлении, при наблюдении в котором ток в рамке представляется текущим по часовой стрелке.

Выражения для вращающего момента , действующего со стороны магнитного поля на магнитный диполь, и потенциальной энергии постоянного магнитного диполя в магнитном поле, аналогичны соответствующим формулам для взаимодействия электрического диполя с электрическим полем, только входят тудамагнитный момент ивектор магнитной индукции :

Магнитный момент кругового тока   сила тока I, текущего по витку, площадь S, обтекаемая током и ориентация витка в пространстве, определяемая направлением единичного вектора нормали   к плоскости витка.

7. Мощность в цепи переменного токамгновенная мощность равна P= , где u и i - мгновенные значения напряжения и тока.Средняя мощность. P= . Пусть u=U_msin t и I_msin(t- ), тогда средняя мощность будет равна P= Величину Iэфф=  называют эффективным, или действующим значением переменного тока; это, фактически, величина постоянного тока, оказывающего такое же действие, как переменный ток с амплитудой I_0. Аналогично вводятся эффективные (или действующие) значения напряжения и э.д.с. Мощность в цепи переменного тока, как видим, зависит от времени; величину N называют ещё мгновенной мощностью;среднее за период значение мгновенной мощности; её называют активной мощностью Р: P=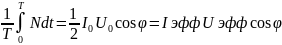 ; cos-R/Z -коэффициентом мощности,При резонансе реактивное сопротивление обращается в ноль; при этом Z = R, cos = 1, то есть на активном сопротивлении (полезной нагрузке) выделяется максимальная мощность.

8 Переменный ток. Характеристика переменного тока, цепь, содержащая активное сопротивление, емкость и индуктивность, резонанс напряжений.

электрический ток называется переменным, если он в течение времени меняет свое направление и непрерывно изменяется по величине.Переменный ток, изменяется по синусоидальному закону :   i = I _m sin (2πft ) Переменный однофазный электрический ток имеет следующие основные характеристики: f – частота переменного тока определяет количество циклов или периодов в единицу времени. За единицу измерения частоты переменного тока принят Герц ( Гц ):Τ – период – время одного полного изменения переменной величины.Если в 1 секунду происходит 1 период Τ, то частота f = 1 Гц ( Герц ).ω – угловая скорость; ω=2πf; Эффективное значение тока – это величина переменного тока, равная такому току, который на сопротивлении R, создаёт тепловыделение равное данному переменному току, за тоже время t (I,U,E,P).

I =

Im √2

U =

Um √2

Рассмотрим цепь, состоящую из последовательно соединенных активного сопротивления R, катушки индуктивности L, конденсатора C и источника переменного напряжения U .Найдем силу тока I, который установится в цепи при напряжении, изменяющемся по закону  . В случае постоянного тока полное сопротивление при последовательном соединении равно сумме сопротивлений всех элементов цепи. Это обусловлено тем, что полная разность потенциалов при последовательном соединении элементов цепи равна сумме падений напряжения на отдельных элементах. В случае переменного тока ситуация более сложная. Ток во всех элементах цепи имеет одно и тоже значение в один и тот же момент времени и одинаковую фазу. Напряжение же на конденсаторе опережает ток по фазе на  п\2 и, следовательно, опережает на п\2 напряжение на сопротивлении, соединенном последовательно с конденсатором. В то же время напряжение на катушке индуктивности отстает по фазе от тока на п\2 и, следовательно, отстает по фазе на п от напряжения на конденсаторе. Поэтому полное напряжение на катушке индуктивности и конденсаторе равно разности напряжений на них и опережает напряжение на сопротивлении по фазе на п\2. Полная разность потенциалов во всей цепи равна сумме этих двух синусоидально изменяющихся напряжений: результирующего напряжения на катушке индуктивности и конденсаторе и напряжения на активном сопротивлении. Такое напряжение тоже меняется по закону синуса, а его амплитуда равна модулю векторной суммы амплитуд напряжений на всех элементах цепи. Резонанс напряжений в цепи переменного тока Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности. Полная компенсация, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда X_L = Х_С или, что то же, когда ωL = 1 / ωС. Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома I = U / R, где вместо Z теперь поставлено R. Одновременно с этим действующие напряжения как на катушке U_L = IX_L так и на конденсаторе Uc = IХ_С окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это явление называется  резонансом напряжений.При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников. 

__________________________________________________________________________________________________________________________________