27. Средняя гармоническая взвешенная

в статистической практике чаще применяется средняя гармоническая взвешенная. Она используется, как правило, при расчете общей средней из средних групповых.

28. Метод укрупнения интервалов

Метод укрупнения интервалов является наиболее простым методом преобразования ряда с колеблющимися уровнями с цепью выявления тренда. Главное в этом методе заключается в преобразовании первоначального ряда динамики в ряды более продолжительных периодов (например, месячные в квартальные, квартальные в годовые и т.д.) Уровнями ряда с укрупненными периодами могут быть средние величины первоначальных уровней по новым периодам. Недостаток метода: резко сокращается количество уровней.

29. Классификация признаков

Основная классификация
по характеру ихвыражения	по способуизмерения	по отношению кхарактеризуемомуобъекту	по характерувариации	по отношению ковремени
1. Описательные	1. Первичные илиучитываемые	1. Прямые(непосредственные)	1. Альтернативные	1. Моментные
2. Количественные	2. Вторичные илирасчетные	2. Косвенные	2. Дискретные	2. Интервальные
			3. Непрерывные

30. Равные и равнонаполненные интервалы

Равные (во всех группах h_i равный) h_i = (х_max - х_min)/n, где х_max - наибольшее значение группировачного признака; х_min - наименьшее значение группировачного признака; n - количество групп.

1. Равнонаполненные интервалы (имеют одинаковое количество единиц):

                m = N / n, где

m – количество групп,

N – количество единиц в совокупности,

n – количество единиц в группе.

31. доверительный интервал для средней

Доверительным называется интервал, который с заданной надежностью  покрывает оцениваемый параметр.

32. Аналитическое выравнивание

 При методе аналитического выравнивания ³ принимаются в расчет закономерные черты динамики явления, и им придается аналитическое выражение. Аналитическое выравнивание производится при помощи известного из математики способа наименьших квадратов ⁴

^{33. статистическая закономерность}

ЗАКОНОМЕРНОСТЬ СТАТИСТИЧЕСКАЯ - такая форма закономерной связи явлений, что вытекающее из нее предсказание носит вероятностный характер. 

34. закрытые и открытые интервалы.

Закрытыминазываются интервалы, у которых имеются обе границы: верхняя и нижняя границы.

Открытые- это интервалы, у которых указана только одна граница: как правило, верхняя - у первого интервала и нижняя - у последнего.

35. дисперсия

Дисперсия - (от лат. dispersio - рассеяние), в математической статистике наиболее употребительная мера рассеивания, отклонения случайных значений от среднего

36. –

37. метод статистики

Метод статистики – это целая совокупность приемов, пользуясь которыми статистика исследует свой предмет. Она включает в себя три группы собственно методов: метод массовых наблюдений, метод группировок, метод обобщающих показателей.

38. ряд распределения

Рядом распределенияназывается упорядоченное распределение единиц совокупностина группы по какому-либо признаку.Виды рядов распределения:

• атрибутивный;

• вариационный;

• дискретный;

• интервальный.

39. формула расчета дисперсии

Дисперсия  - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия простая:

В нашем примере: 

Дисперсия взвешенная:

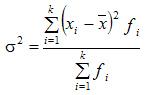
Более удобно вычислять дисперсию по формуле:

40. линейная и нелинейная связь

СВЯЗЬ СТАТИСТИЧЕСКАЯ ЛИНЕЙНАЯ - вид статистической связи между двумя или несколькими количественными переменными

СВЯЗЬ СТАТИСТИЧЕСКАЯ НЕЛИНЕЙНАЯ - статистическая связь (см.) между двумя или несколькими количественными переменными (см.), не являющаяся линейной.

41. статистическое наблюдение

Статистическое наблюдение – это первая стадия всякого статистического исследования, представляющая собой научно организованный по единой программе учет фактов, характеризующих явления и процессы общественной жизни, и сбор полученных на основе этого учета массовых данных.

42. ранжирование ряда

Ранжирование - это процесс преобразования простого статистического ряда на основе упорядочения (группирования) числовых значений элементов ряда по убыванию

43. размах вариации

РАЗМАХ ВАРИАЦИИ - Мера разброса значений выборки наблюдений или распределения, рассчитываемая как разность между максимальным и минимальным значениями переменной

44. Функциональная, случайная и стохастическая связь

Как известно, случайные величины X и Y могут быть либо зависимыми, либо независимыми. Существуют следующие формы зависимости – функциональная и статистическая. В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y=f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

При стохастической связи причинная зависимость между факторными и результативными признаками проявляется не в каждом отдельном случае, а лишь при большом числе наблюдений. В каждом конкретном случае при изменении одной переменной вторая может принимать в определенных пределах любые значения с некоторой вероятностью.