1. Статистика как наука.

Статистика считается математической наукой, относящейся к сбору, анализу, интерпретации, объяснения, и представления данных. Кроме этого статистика занимается предсказанием и прогнозированием на основе исходных данных. Статистика применима в широком кругу научных дисциплин, от естественных и социальных наук заканчивая гуманитарными, в государственной экономике и бизнесе.

2. Структурная группировка.

Структурная дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги.

3. Средняя арифметическая простая

Средняя арифметическая – самый распространенный вид средней величины. Когда речь идет о средней величине без указания ее вида, подразумевается именно средняя арифметическая. Она исчисляется в тех случаях, когда объем усредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности

4. квартили

КВАРТИЛИ

— значения случайной переменной, делящие распределение на 4 равные по объему части. К. обычно находят графически, опуская перпендикуляры на ось абсцисс из точек нарастающей кривой, отвечающих 25% (Q₁), 50% (Q₂) и 75% (Q₃) ординатам. При шкале, увеличивающейся по оси абсцисс слева направо, Q₁<Q₂<Q₃. К., отвечающая 50% ординате (Q₂) называется медианой.

5. Метод скользящей средней

Наиболее простым способом выявления линии трен­да служит механическое выравнивание динамического ряда, или, как его еще называют, метод скользящей "средней

6. Предмет статистики

Предметом статистики служит количественная сторона массовых явлений любой области в неразрывной связи с их качественным содержанием. При этом количественное выражение закономерностей развития этих явлений осуществляется с учетом конкретных условий места и времени.

7. Аналитическая группировка

 

- статистическая группировка, предназначенная для изучения взаимосвязей между признаками. Аналитическая группировка строят по одному из взаимосвязанных признаков, например факторному, а далее вычисляют по каждой выделенной группе средние (или относительные) значения другого признака (в нашем случае результативного). Параллельно сопоставляя значения обоих признаков по характеру их совместных изменений, делают заключение о наличии и направлении связи.

8. Средняя арифметическая взвешенная

Средняя величина является обобщающей характеристикой совокупности по качественно однородному признаку и показывает типичный уровень изучаемой совокупности.

9. децили

ДЕЦИЛЬ

- значение х, при котором непрерывная строго монотонная функция распределения F(x)принимает для j=1, 2,. .., 9 значения, равные j/10. Когда Д. существуют, они дают хорошее представление о форме кривой распределения. Расстояние между девятой и первой Д. наз. интердецильной широтой, она дает представление о рассеянии распределения. Д.- частный случай квантил

10. статистическая совокупность

Статистическая совокупность - совокупность объектов или явлений одного и того же вида, объединенных определенным признаком.

11. фактический и результативный признаки

При изучении конкретных зависимостей выявляют факторные и результативные признаки. В корреляционных связях между изменениями факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных.

12. средняя геометрическая простая

Средняя геометрическая Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака представляют собой относительные показатели динамики, построенные в виде цепных величин, как отношения каждого уровня к предыдущему. Средняя геометрическая простая рассчитывается по формуле: ,

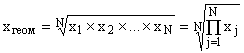13. средняя геометрическая простая

Средняя геометрическая Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака представляют собой относительные показатели динамики, построенные в виде цепных величин, как отношения каждого уровня к предыдущему. Средняя геометрическая простая рассчитывается по формуле: , где  –  знак произведения,  N   –  число осредняемых величин.

14. выборочное наблюдение

Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.

15. средний темп роста

Средний темп роста

Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.

16. единица статистической совокупности

Статистическая совокупность состоит из единиц совокупности. Каждая единица совокупностипредставляет собой частный случай проявления изучаемой закономерности.

17. группировочный признак

Группировочный признак – это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы.

18. средняя геометрическая взвешенная

Взвешенная средняя величинарассчитывается посгруппированнымстатистическим величинам с использованием следующей общей формулы:

где X – значения отдельных статистических величин или середин группировочных интервалов; m - показатель степени, от значения которого зависят следующие виды степенных средних величин: при m = 0 средняя геометрическая;

19. виды выборочного наблюдения

Существует 4 способа случайного отбора в выборку:

1. Собственно случайный отбор , когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад.

2. Механический отбор, согласно которому отбирается каждая (N/n)-я величина генеральной совокупности. Например, если она содержит 100 000 величин, а требуется выбрать 1 000, то в выборку попадет каждая 100 000 / 1000 = 100-я величина.

3. Отбор величин из неоднородного массива данных ведется стратифицированным (расслоенным) способом, когда генеральная совокупность предварительно разбивается на однородные группы, к которым применяется случайный или механический отбор.

4. серийный отбор, при котором случайно или механически выбирают не отдельные величины, а их серии (последовательности с какого-то номера по какой-то подряд), внутри которых ведут сплошное наблюдение.