МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПЕЧАТИ

Факультет Полиграфической техники и технологии

Дисциплина: Математика

Курсовая работа по теме

«Статистические методы обработки

Экспериментальных данных»

Выполнила: Семенов а.А

курс 2

группа ДТпм-2-1

форма обучения дневная

Номер зачётной книжки

Вариант № 10

Допущено к защите

Дата защиты

Результат защиты

Подпись преподавателя

Москва - 2008

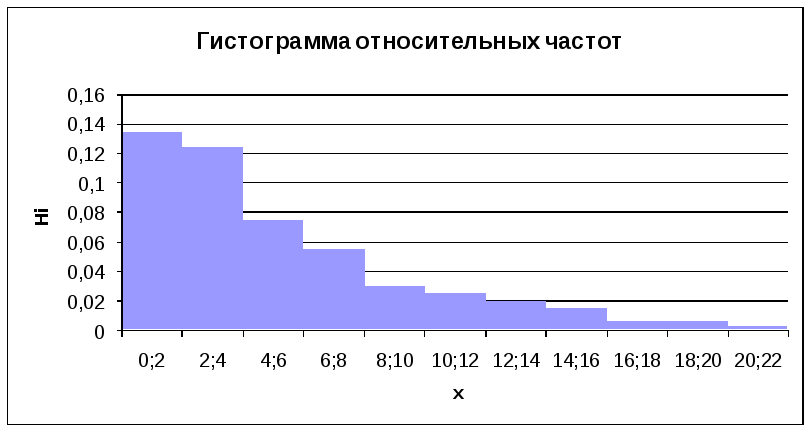
1. Интервальное и точечное статистические распределения результатов наблюдений.

- интервал разбиения;

- середина интервала ;

- частота;

- относительная частота (-объем выборки);

-плотность относительной частоты (h=2 - шаг разбиения, т.е. длина интервала)

	1;3	3;5	5;7	7;9	9;11	11;13	13;15	15;17	17;19	19;21	21;23
	26	24	21	20	13	8	8	4	3	2	1
	2	4	6	8	10	12	14	16	18	20	22
	0,2	0,185	0,162	0,154	0,1	0,062	0,062	0,031	0,023	0,015	0,008
	0,1	0,093	0,081	0,077	0,05	0,031	0,031	0,016	0,012	0,0075	0,004

2. Нахождение точечных оценок математического ожидания и дисперсии.

-исправленная дисперсия

I	1	2	3	4	5	6	7	8	9	10	11
	2	4	6	8	10	12	14	16	18	20	22
	26	24	21	20	13	8	8	4	3	2	1
	52	96	126	160	130	96	112	64	54	40	22
	735,86	264,54	36,59	9,25	93,37	175,22	356,98	301,37	342,19	321,56	205,52

∑ =952; ∑ =2842,72

MX =7,323

DX =22,034

3. Выдвижение гипотезы о распределении случайной величины.

а) Нормальное (или гауссовское) распределение с параметрами «а» и «» , где

б) Показательное (или экспоненциальное) распределение с параметрами и , где

при

при

в) Равномерное распределение на отрезке [А;В], где

при

при x<A и x>B

Сравнение построенной гистограммы и графиков плотностей основных распределений приводит к заключению о том, что изучаемая случайная величина имеет показательное распределение.

4. Построение графика теоретической плотности распределения.

=0,213

=7,323-4,694=2,629

Следовательно плотность предполагаемого распределения задаётся формулой:

Теперь необходимо вычислить значения теоретической плотности f(x) при x=x₀ (т.е. значение «в параметре сдвига») и при x=x_i , где x_i > x₀

(т.е. значения в серединах интервалов, больших x₀ ). Для этого воспользуемся следующей схемой:

xj	uj	e-uj	F(xj)= e-uj
2.629	0,00	1,0000	0,2130
4	0,29	0,7497	0,1597
6	0,79	0,4563	0,0972
8	1,22	0,2977	0,0634
10	1,65	0,1942	0,0414
12	2,08	0,1267	0,0270
14	2,5	0,0835	0,0178
16	2,92	0,055	0,0117
18	3,35	0,0359	0,0076
20	3,78	0,0234	0.0050
22	4,20	0,0154	0,0033

Гистограмма и график теоретической плотности распределения

5. Проверка гипотезы о распределении с помощью критерия согласия Пирсона.

5.1 группировка исходных данных

	+∞:5	5;7	7;9	9;11	11;13	13;15	15;17	17;∞
	24	21	20	13	8	8	4	6

5.2 вычисление теоретических частот

-теоретические частоты

Т.к. принята гипотеза о показательном распределении с.в., то теоретическая вероятность вычисляется по одной из следующих формул в зависимости от взаимного расположения i-ого промежутка и числа x₀ :

N=150=139

=0,2219=0,213

X₀=0,746=2,629

i	Концы промежутков
1		5	0	0,5050	1	0,6056	0,3944	51,272
2	5	7	0,5050	0,9310	0,6056	0,3774	0,2282	29,666
3	7	9	0,9310	1,4717	0,3774	0,2318	0,1456	18,928
4	9	11	1,4717	1,7830	0,2318	0,1702	0,0616	8,008
5	11	13	1,7830	2,2090	0,1702	0,1115	0,0587	7,631
6	13	15	2,2090	2,6350	0,1115	0,0730	0,0385	5,005
7	15	17	2,6350	3,0610	0,0730	0,0478	0,0252	3,276
8	17		3,0610		0,0478	0	0,0478	6,214

0. статистика и вычисление её значения по опытным данным

;

I
1	24	51,272	14,506202
2	21	29,666	2,531503
3	20	18,928	0,060713
4	13	8,008	3,111896
5	8	7,631	0,017843
6	8	5,005	1,792213
7	4	3,276	0,160005
8	6	6,214	0,007370

 130 130 22,19

22,19 -наблюдаемое значение критерия

- уровень значимости (задан в условии)

r=L-N-1=5-число степеней свободы (L=8- количество промежутков разбиения, N=2- количество параметров предполагаемого разбиения)

=11,07- критическое значение (находится по таблице)

Вывод: гипотеза (о показательном распределении) неверна, поскольку

>

6