17) Геометрическая и энергетическая интерпретация уравнения Бернулли

в геометрическом смысле каждый из членов уравнения выражает высоту (напор), что легко доказать проанализировав размерность каждого члена,

•      z - геометрический напор    ="м

•      p/ρg - пьезометрический напор = (Н/м2) / (Н/м3) = м

•      z +p/ρg - гидростатический напор

•    V2/2g - скоростной напор = (м2/с2)/ (м/с2) = м

•   hn - потери напора = м

Сумма всех составляющих - полный напор.

Энергетический смысл:

в энергетическом смысле каждый из членов уравнения выражает величину удельной энергии потока, т.е. энергию, приходящуюся на единицу массы движущейся жидкости,

•       z - удельная потенциальная энергия положения

•       p/ρg - удельная потенциальная энергия давления

•       z +p/ρg - удельная потенциальная энергия

•       V2/2g - удельная кинетическая энергия

•       hn - потери удельной энергии

Сумма всех составляющих - полная удельная энергия. Следовательно, энергетический смысл можно выразить так: при установившемся движении потока реальной жидкости сумма четырех удельных энергий остается неизменной вдоль потока.

18) Потери напора. Гидравлическое сопротивление.

Потери напора – это часть удельной механической энергии потока, теряемое на преодоление сил сопротивления. Бывают: 1)потери напора по длине. 2) Местные потери напора. Общие потери напора h=

Виды гидравлических сопротивлений: 1) Вязкостные сопротивления – возникают в ламинарном движении жидкости из-за её свойства сопротивляться касательным усилиям. 2)Инерционные сопротивления- образуются из-за образования вихрей и перемешивания масс жидкостей в турбулентном режиме движения.

19) Гидравлический коэффициент трения.

При равномерном движении жидкости в трубах потери давления на трение как при ламинарном, так и при турбулентном режимах движения рассчитывают по формуле Дарси–Вейсбаха:

λ где λ – коэффициент гидравлического трения; l – длина трубопровода;  d – его внутренний диаметр; V – средняя скорость потока жидкости. Коэффициент гидравлического трения зависит от режима движения жидкости, значения критерия Рейнольдса

21) Гидро расчет коротких трудопроводов

Коротким называется трубопровод, при расчете которого учитываются местные потери напора, а уравнение Бернулли применяется в канонической форме. Это целесообразно делать в случаях, когда доля местных потерь напора велика. Поэтому практически трубопровод считается коротким, если в нем местные потери напора превышают 10 % в общих потерях напора. Имеются три основных типа задач при гидравлическом расчете коротких трубопроводов: 1. Определение напора (давления) в начале потока и (или) в других его сечениях при заданном расходе и известных геометрических размерах установки. 2. Определение расхода при заданных геометрических размерах установки и известном действующем напоре. 3. Определение длины или диаметра трубопровода при заданных значениях расхода, напора и геометрической схемы установки.

Расчет необходимо начать с определения формы записи уравнения Бернулли. Для расчета систем водоснабжения и водоотведения обычно применяется уравнение Бернулли в форме напоров:

.

Расчет трубопровода фактически сводится к расчету потерь – местных и по длине. В коротком трубопроводе потери напора по длине определяются по формуле:

• для ламинарного режима коэффициент гидравлического трения определяется по формуле:

,

• для турбулентного режима коэффициент гидравлического трения рассчитывается по формуле:

.

Потери напора на местном сопротивлении при турбулентном режиме определяются по формуле:

Если режим движения ламинарный, то потери напора на местном сопротивлении определяются по формуле:

,

После расчета потерь напора по длине и на местных сопротивлениях строятся линии полного и пьезометрического напоров. Для этого трубопровод разбивается на сечения. Количество сечений зависит от количества прямолинейных участков трубопровода и местных сопротивлений. Полный напор в начальном сечении трубопровода определяется по формуле:

.

22)Гидро расчет длинных трубопроводов.

   Расчет сводится к определению суммарных потерь напора по длине трубопровода, так как местными потерями пренебрегают

.

          Преобразуем выражение для потери напора по длине

,

где   - расходная характеристика.

          Тогда

.

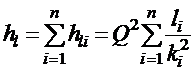          Формула показывает, что трубопровод, составленный из последовательно соединенных труб разного диаметра и длины, можно рассматривать как простой трубопровод, суммарные потери напора, в котором равны сумме потерь напора составляющих его труб.

          Формула позволяет решить и обратную задачу, т.е. при заданных напоре, диаметре труб вычислить расход Q :

.

23)

Сельскохозяйственные водопроводы в настоящее время обычно имеет разветвленную тупиковую сеть наружных трубопроводов. Кольцевые сети пока еще применяются реже.

Местные потери напора в водопроводах малы (не превышают 10 % от потерь напора по длине), поэтому их гидравлический расчет ведется по правилам длинных трубопроводов.

Расчет основан на применении уравнения Бернулли:

, (3.33)

где Н_н — действующий напор в начале рассматриваемого участка трубопровода;

Н_к — действующий напор в конце данного участка трубопровода;

h_н-к — общие потери напора (по длине и местные) на данном участке Н–К.

При расчете длинных трубопроводов, предназначенных для водоснабжения, потенциальный напор Н_п = z + р/ определяется из зависимости, вытекающей из схемы (рисунок 3.9):

(3.34)

где  — геодезическая отметка местности в рассматриваемом узле, представляющая собой высоту местности над плоскостью сравнении0–0 (рисунок 3.9). Если за плоскость сравнения принимается средний уровень Балтийского моря, то отметки называются абсолютными; если другой уровень, то отметки называются условными;

Н_св — действующий свободный напор в данном узле (удельная энергия давления p/, отсчитываемая от поверхности земли (рисунок 3.9).

Скоростной напор при расчетах не учитывается вследствие его малости по сравнению с потенциальным, поэтому действующий напор H в каждом узле выражается соотношением (рисунок 3.9):

(3.35)

Такой метод определения напоров для уравнения Бернулли позволяет исключить из расчетов глубину укладки трубопровода под землей. Эта глубина в природных условиях Беларуси может изменяться в широких пределах.

Рисунок 3.9 — Напоры

Рисунок 3.10 — Схема водопроводной сети

Потери напора h при расчете длинных трубопроводов вычисляются по формуле:

(3.36)

где Q — расчетный расход на рассматриваемом участке трубопровода;

К — модуль расхода (в справочниках обычно приводится К² или удельное сопротивление А = 1/К² );

l — длина рассматриваемого участка трубопровода;

 — коэффициент, учитывающий отличие скорости в трубопроводе от той, для которой составлены таблицы К² или A;

j — коэффициент, учитывающий местные потери напора. По СНиП 2.04.02–84 j = 1,1–1,2.

Напор в трубопроводах, который создается башней или насосом, должен быть таким, чтобы все технические устройства водопотребителей (автопоилки, водоразборные колонки, вентили и т. п.) работали нормально, т. е. обеспечивали подачу нужного расхода воды.

Наименьший напор, при котором обеспечивается нормальная работа технических устройств водопотребителей, называется необходимым напором H.

В справочниках приводится необходимый свободный напор H_св, который представляет собой удельную энергию давления p/, отсчитываемую от поверхности земли, необходимую для нормальной работы, соответствующих технических устройств водопотребителей. Необходимый свободный напор учитывает высоту расположения устройств над поверхностью земли, а также потерю напора в них и во внутренних трубопроводах.

Необходимый напор определяется по формуле (3.34), принимающей вид:

(3.37)

Из выше сказанного следует, что для нормальной работы технических устройств водопотребителей необходимо, чтобы во всех узлах сети выполнялось условие:

(3.38)

Наиболее экономичным является решение, когда напор, создаваемый водонапорной башней или насосами и уменьшающийся из-за гидравлических сопротивлений по мере продвижения по трубам, будет обеспечивать равенство действующего и необходимого напоров по крайней мере в одном узле. Этот узел называется диктующей точкой. Таким образом, для диктующей точки выполняется условие:

(3.39)

а в других узлах сети действующий напор больше необходимого, т.е.

(3.40)

Участок водопроводной сети от начала (от водонапорной башни) до диктующей точки называется главным направлением. Участки сети, отходящие от главного направления, называются отводами.

Исходными данными при расчете наружных трубопроводов систем водоснабжения (в том числе и сельскохозяйственных) являются следующие.

1. Схема сети (рисунок 3.10).

2. Путевые Q_п, и узловые Q расходы, которые определяются в зависимости от количества и вида потребителей. Путевой расход характеризует отбор воды из многих сечений (точек) участка трубопровода, а узловой — только из одного сечения (точки).

В некоторых случаях вместо путевого известной величиной является удельный расход q, который представляет собой расход, идущий потребителю с одного погонного метра трубопровода.

Удельный и путевой расход на участке длиной l связаны между собой соотношением:

(3.41)

3. Высотное положение  узловых точек и длина трубопроводов между ними, которые находятся в соответствии с планом местности и схемой сети.

4. Необходимый свободный напор H_св, который как указывалось выше, определяется видом технических устройств водопотребителей и их высотным положением относительно поверхности земли.

В результате расчета водопроводной сети определяются диаметры трубопроводов, действующие напоры во всех узлах, высота водонапорной башни или напор насоса.

24) При истечении жидкости из какого-либо резервуара происходит процесс превращения запаса потенциальной энергии в кинетическую энергию свободной струи. Основной вопрос исследования – определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.

Рассмотрим истечение жидкости через круглое отверстие в тонкой стенке (рис. 4.20). Отверстием в тонкой стенке называется отверстие, толщина стенок которого составляет не более 1/4 диаметра. Рассмотрим случай, когда жидкость вытекает из резервуара в атмосферу (см. рис. 4.20). Напишем уравнение энергии в форме напоров для сечения 1-1 и С-С. Обозначим давление на поверхности жидкости в резервуаре p₀,   – заглубление центра отверстия под уровнем жидкости в сосуде. Струя, вытекающая под давлением столба жидкости высотой   и разностью давлений  , при выходе из отверстия сжимается до сечения С-С. В сечении С-С струйки приблизительно параллельны и движение можно считать плавноизменяющимся, поэтому для этого сечения можно применить уравнение Бернулли. Такое сжатие обуславливается инерцией частиц жидкости, движущихся при подходе к отверстию по криволинейным траекториям. Степень сжатия струи оценивается коэффициентом

,

(4.21)

Рис. 4.20. Истечение жидкости из отверстия в тонкой стенке

где  – отношение площади струи в сжатом сечении к площади отверстия.

Для плоскости сравнения, проведенной относительно оси отверстия, запишем уравнение Бернулли для движения жидкости от свободной поверхности, где скорость можно принять равной нулю, до сечения С-С

,

где  – коэффициент сопротивления отверстия.

Выполним небольшие преобразования

 или  ,

где H – расчетный напор

.

(4.22)

Скорость истечения

,

(4.23)

где φ– коэффициент скорости.

Нами получена формула Торричелли для определения скорости струи, вытекающей из резервуара.

Если резервуар открыт, то , тогда

и  .

(4.24)

Расход через сжатое сечение

,

где ε – коэффициент сжатия струи;   – площадь сечения отверстия.

Окончательно получаем:

,

(4.25)

где μ – коэффициент расхода.