Шпаргалка По Высшой Математике (Афанасьева С. Г.) / 50.Формула Тейлора для нескольких переменных

50.Формула Тейлора для функции нескольких переменных.

Напомним, что в случае функции одного переменного формула Тейлора имеет вид

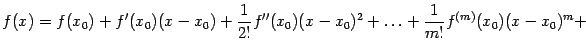
где x₀ - фиксированная точка, в которой ведётся разложение, x - текущая точка, а x_t - некоторая точка отрезка между точками x₀и x. При этом предполагается, что функция f имеет производную (m + 1)-го порядка, определённую в некоторой окрестности точки x₀.

Последнее слагаемое формулы, то есть называется остаточным членом формулы Тейлора, а многочлен от x, равный

называется многочленом Тейлора функции f в точке x₀.

Наша цель - получить формулу для функции f, зависящей от n переменных x₁…x_n, частным случаем которой при n = 1 будет выписанная выше формула Тейлора для функции одного переменного.