Шпаргалка По Высшой Математике (Афанасьева С. Г.) / 45.Свойства функций, дифференцируемых на интервале

45.Свойства функций дифференцируемых на интервале: Теорема: Ролля, Коши, Лагранжа.

Теорема: Ролля

Рассмотрим функции имеющие конечную производную на интервале .

Теорема

Если функция y=f(x) непрерывна на отрезке (ab) и значения функции на концах отрезка одинаковые то существует хотябы одна точка что производная в этой точке равна нулю

Доказательство.

Тогда рассмотрим преращения

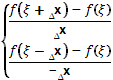
F’(

• f’( ч т д

F’(

Теорема: Коши

Если функция F(x) и непрерывны на отрезке ab деференцируемы на интервале ab причем 0 то для всех значений х из отрезка ab существует хотябы одна точка из этого отрезка такая что выполняется правило

= (1)

Y=f(x) F(x)⋁f(x)⋀(x)⋀(x)0 => x(a,b) (a,b) => (1)

Доказательство

Лямда выбирается так:

F(x)=f(x)+ => F(a)=F(b)

F(a)=f(a)+

F(b)=f(b)+

F(a)+

=-

Всегда существует т.к.

Подставим х в F(x)

F(x)=f(x)-

F(x) (непрерывная функция) ⋀F(x) => ⋀F(a) F(b) =>

F’(=f’(

= чтд

Теорема: Лагранжа.

Если f(x) непрерывна на отрезке ab и дифференцируема на ab то существует хотя бы одна точка такая что f(b)-f(a)=f’((b-a)

F(x)⋀f(x)=>

Доказательство

=x =1 =b =a

Подставим в (1)

=

F(b)-f(a)=f’((a-b) ч.т.д