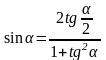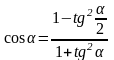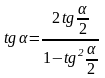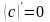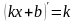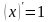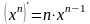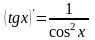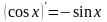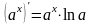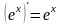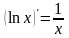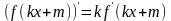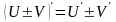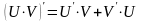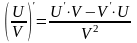- •Бюджетное профессиональное образовательное учреждение Вологодской области «Череповецкий химико-технологический колледж»
- •Содержание
- •Аннотация
- •Пояснительная записка
- •Формулы сложения аргументов
- •Алгоритм составления уравнения касательной
- •На отрезке [а; в]
- •Степени и корни
- •Уравнение вида имеет решения:
- •Алгоритм решения показательных неравенств
- •Первообразная и интеграл
- •Бином Ньютона
- •Член разложения бинома Ньютона
- •Треугольник Паскаля
- •Теорема Бернулли
- •Уравнения и неравенства
- •Геометрия Многогранники
- •Список литературы
Формулы сложения аргументов
|
|
|
|
|
|
|
|
Простейшие тригонометрические уравнения и частные случаи
sin
t
= a
,
t
= ( -1) n
arcsin
a + πn,
n
Частные случаи: sin
t = 1 ,
t =
sin t = - 1 , t = - + 2πn , n sin t = 0 , t = πn , n
|
cos t = a , t = ± arccos a + 2πn, n
Частные случаи: сos t = - 1, t = π + 2πn, n cos t = 0 , t = + πn , n cos t = 1 , t = 2πn, n
|
tg t = a t = arctg a + πn, n
Частные случаи: tg
t = 1 ,
t =
tg t = - 1 , t = - + πn , n tg t = 0 , t = πn , n |
ctg t = a t = arcctg a + πn, n
Частные случаи: ctg t = 1 , t = + πn, n ctg
t = - 1 ,
t =
ctg t = 0 , t = πn , n |
Формулы двойного угла
sin2α
= 2sinα |
cos2α = cos2 α – sin2 α |
cos2α = 2cos2 α – 1 = 1 – 2sin2 α |
|
|
|
Формулы сложения одноимённых функций
sinα+sinβ
= 2sin |
cosα+cosβ=
2cos |
sinα – sinβ = 2sin cos |
cosα–cosβ=-2sin |
|
|
Формулы половинного угла
|
|
sinα
= 2sin |
cosα = cos2 – sin2 |
cosα =2cos2 – 1 = 1 – 2sin2 |
|
|
|
|
|
Преобразование произведения тригонометрических функций
в алгебраическую сумму
|
|
|
Производная. Применение производной
Таблица производных
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(производная сложной функции) |
||
Правила дифференцирования |
||
|
|
|
|
|
|
Алгоритм составления уравнения касательной
к графику функции у = f(х) в точке х = а.
Обозначим абсциссу точки касания буквой а.
Вычислим f(a).
Найдем f '(х) и вычислим f '(а).
Подставим значения числа а, f(а), f '(а) в уравнение касательной.
Записать получившееся уравнение y = f(a) + f '(а) · (x-a) и привести к виду у = kx+b.
Геометрический смысл производной функции у = f(х).
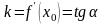 (
( –
угловой коэффициент)
–
угловой коэффициент)

Схема исследования функции
Область определения функции
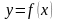 .
Обозн.
.
Обозн.
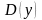
Исследование функции на чётность и нечётность:
если
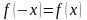 ,
то функция чётная
(симметрия относительно оси ОУ)
,
то функция чётная
(симметрия относительно оси ОУ)если
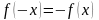 ,
то функция нечётная
(симметрия относительно начала
координат)
,
то функция нечётная
(симметрия относительно начала
координат)если оба условия не выполняются, то функция – ни чётная и ни нечётная (функция общего вида)
Определение точек пересечения с осью х:
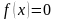
Определение точек пересечения с осью y:
 ,
,

Промежутки возрастания и убывания функции:
находим производную функции
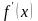
находим критические точки
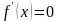
если
 на промежутке, то функция возрастает
на этом промежутке
на промежутке, то функция возрастает
на этом промежуткеесли
 на промежутке, то функция убывает
на этом промежутке
на промежутке, то функция убывает
на этом промежуткеТочки экстремума:
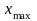 ,
,
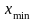 ,
экстремумы функций
,
экстремумы функций
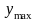 ,
,
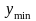 .
.Контрольные точки.
Построение графика функции .
Наибольшее и наименьшее значения функции y = f(x)



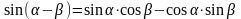
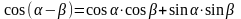
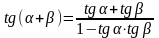
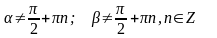
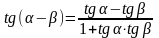

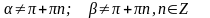
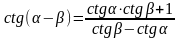
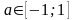
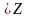
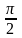 + 2πn,
n
+ 2πn,
n
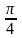 + πn,
n
+ πn,
n
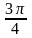 + πn
, n
+ πn
, n
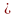 cosα
cosα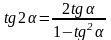
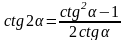
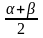 cos
cos

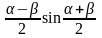
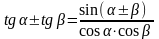

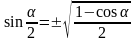
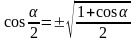
 cos
cos