Моделирование периодического штрихового изображения. Метод Фурье-преобразования. Пространственно-частотный анализ.
Очень часто в полиграфии мы имеем дело с периодическими решетками. Для этих периодических решеток можно использовать метод Фурье-преобразования.
Любая периодическая функция может быть разложена в ряд Фурье.
Эта функция может
быть разложена в ряд:
-
это частота решетки, если мы рассматриваем
пространственную решетку.
Обратное
Фурье-преобразование:
В данной формуле
коэффициент
определяется как интеграл:
коэффициент
определяется
как
и коэффициент
как
;
где
1,
2, 3, 4, …
Учитывая, что
разница между cos
и sin
только в
:
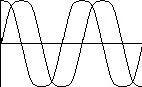
И в векторной
форме:
,
;
,
.
Подставляя сюда наше выражение:
Мы знаем, что по
формуле
Отсюда получаем:
А также используя
формулу Эйлера:
На основе формулы Эйлера мы можем записать нашу формулу:
В этом выражении
Таким образом мы совершили спектральный или гармонический анализ, в котором функция представлена в виде набора составляющих, отличающихся между собой по преобразованной частоте и амплитуде. Величины определяются по ним.
Сами гармонические
составляющие отличаются между собой в
целое число раз; причем каждая имеет
свою амплитуду, отличающую
,
,
.
Представление ряда Фурье в виде дискретных функций
Имея периодическую
функцию:
При чем
- это первая гармоника. При преобразовании
Фурье в пространственный дискретный
ряд, мы нашу амплитуду выражаем дискретными
значениями.
Мы имеем первую
или основную гармонику. При частоте
мы уже можем отложить амплитуду первой
гармоники:
Все гармоники
отличаются в целое число раз. Между
и
- целое число, которое между
и
;
и
всегда одинаково.
Ряд является
бесконечным и меняется от 1 или 0 до
.
Но мы этот ряд можем ограничить числом
членов, так как остальные пренебрежительно
малы.
Бывает так, что отсутствуют либо четные, либо нечетные гармоники.
Если х и –х по
модулю равны, то, то наша функция –
четная – симметричная относительно
оси х. Поэтому она теряет
-составляющую;
т. е. cos-Фурье
составляющие равны нулю; остаются только
sin-Фурье составляющие.
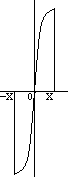
Если периодическая
функция – нечетная – симметрична
относительно оси у, то наш ряд теряет
-составляющую;
т. е. cos
sin -Фурье составляющие равны нулю;
остаются только cos
-Фурье составляющие.
Ряды Фурье.
Обладают тем преимуществом, что он обладает наибольшей точностью при представлении функции, ограниченной числом членов. Ошибки являются минимальными. Другое преимущество – если мы эту функцию представляем разными членами ряда и их недостаточно; то мы добавляем число, но предыдущие члены ряда при добавлении не изменяются. И третье преимущество – это возможность упрощения ряда Фурье для четных функций.
Выше мы рассмотрели разложение функции в ряд Фурье. Это прямое преобразование ряда Фурье. Также мы можем получить обратное преобразование ряда Фурье.
Рассмотрим пример обратного Фурье-преобразования для прямоугольной решетки с п-образным распределением освещенности и с равной шириной штриха и просвета.
при
при
