
- •Задачник-практикум по линейной алгебре
- •Часть I.
- •6.1. Краткие теоретические сведения 54
- •Тема 1. Матрицы. Операции над матрицами
- •1.1. Краткие теоретические сведения
- •1.2. Пример выполнения заданий практической части
- •1.3. Задания для аудиторного занятия
- •1.4. Домашнее задание
- •Тема 2. Определители n-го порядка. Методы вычисления определителей n-го порядка
- •2.1. Краткие теоретические сведения
- •1. Вычисление определителей второго порядка по определению.
- •2. Вычисление определителей третьего порядка по определению (правило треугольника).
- •3. Приведение определителя к треугольному виду.
- •4. Разложение определителя по элементам некоторых строк (столбцов).
- •5. Метод понижения порядка определителя.
- •2.2 . Пример выполнения заданий практической части
- •2.3. Задания для аудиторного занятия
- •2.4. Домашнее задание
- •Тема 3. Нахождение обратных матриц. Решение матричных уравнений.
- •3.1. Краткие теоретические сведения
- •3.2. Пример выполнения заданий практической части
- •3.3. Задания для аудиторного занятия
- •3.4. Домашнее задание
- •Тема 4. Ранг матрицы
- •4.1. Краткие теоретические сведения
- •4.2. Пример выполнения заданий практической части
- •5.2. Пример выполнения заданий практической части
- •5.3. Задания для аудиторного занятия
- •5.4. Домашнее задание
- •Тема 6. Решение систем линейных уравнений методом Гаусса. Фундаментальная система решений
- •6.1. Краткие теоретические сведения
- •6.2. Пример выполнения заданий практической части
- •6.3. Задания для аудиторного занятия
- •6.4. Домашнее задание
5.2. Пример выполнения заданий практической части
Пример 1. Исследовать систему уравнений на совместность:

Решение. Выписываем расширенную матрицу системы:
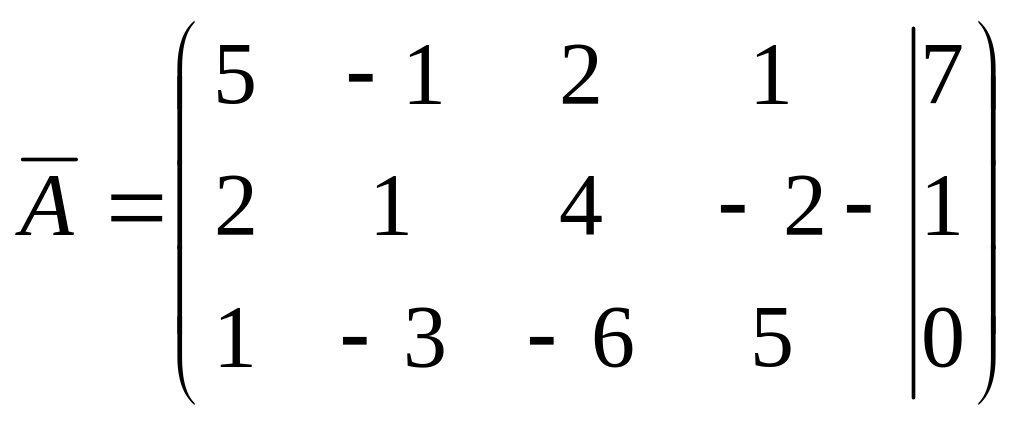
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу
![]()
содержащие его миноры третьего порядка равны нулю:
 ;
;
Следовательно, ранг основной матрицы системы равен 2, т.е. r(A)=2. Для вычисления ранга расширенной матрицы рассмотрим окаймляющий минор
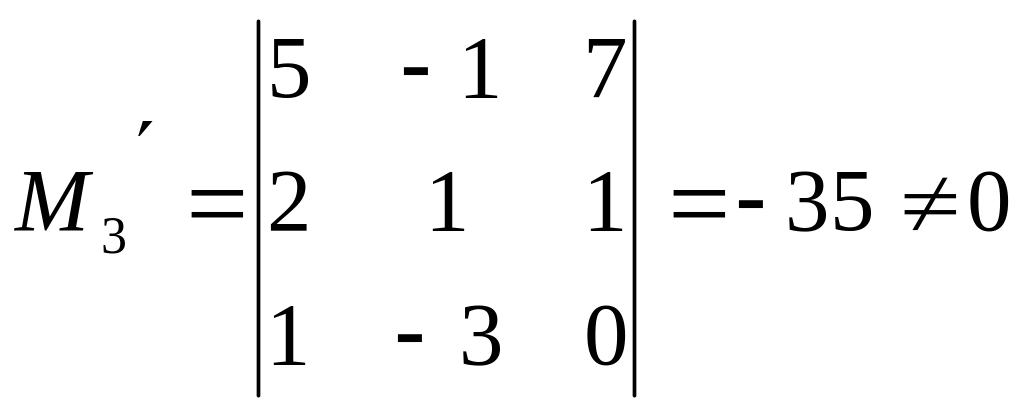
Значит, ранг расширенной матрицы r( ) = 3. Поскольку r(A) ≠ r( ), то система несовместна.
Пример
2. Решить
систему матричным способом:
![]()
Решение.
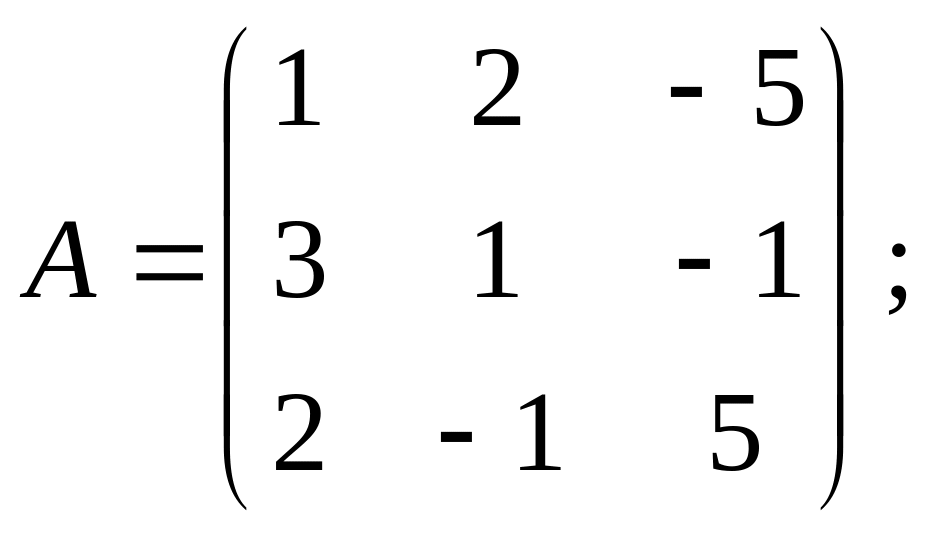
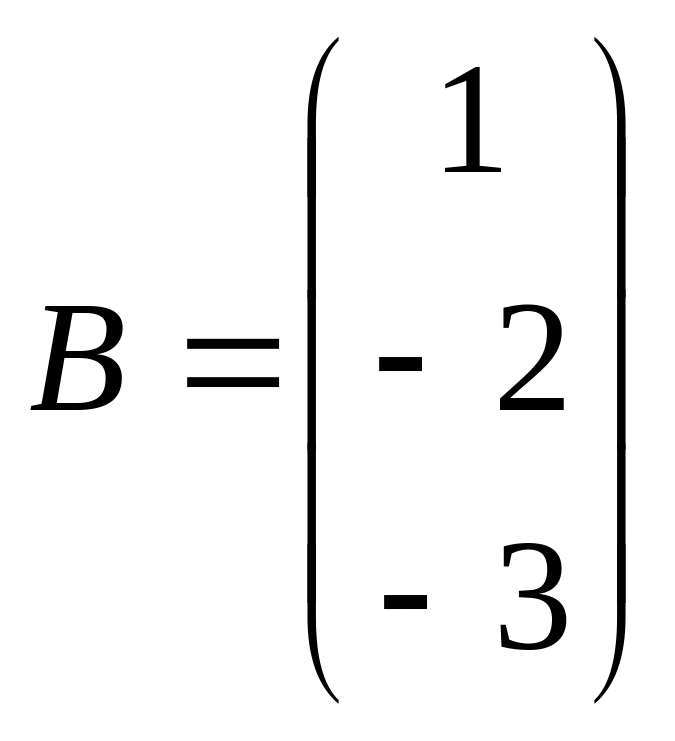 .
.
АХ = В; Х = А-1 × В.
 .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
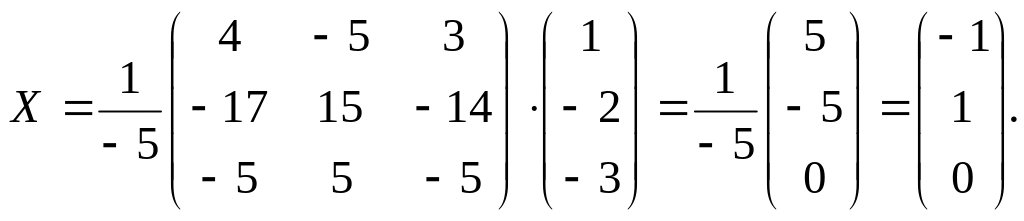
Пример 3. Решить систему уравнений, воспользовавшись формулами Крамера (4.4):
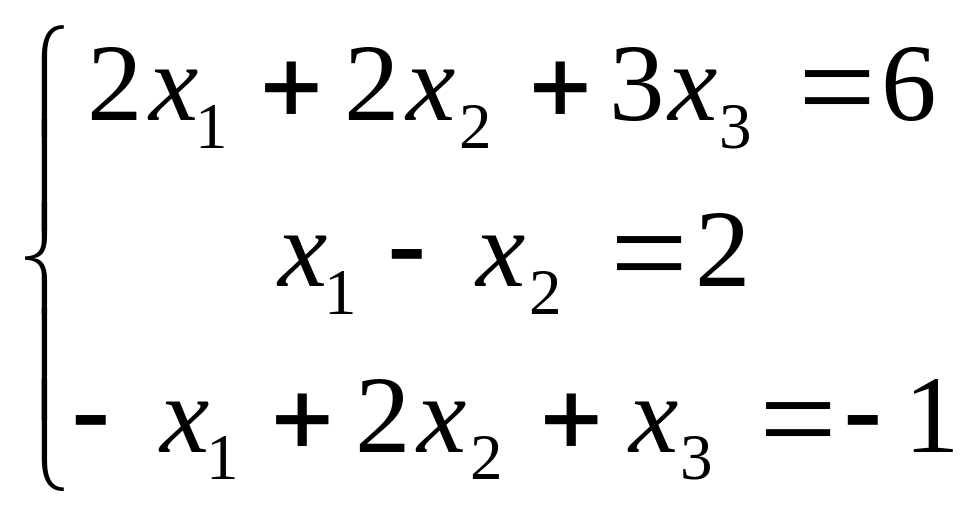
Решение.
Определитель данной системы
 .
.Найдем определитель
 ,
заменив в определителе
первый столбец, столбцом свободных
членов:
,
заменив в определителе
первый столбец, столбцом свободных
членов:
 .
.Найдем определитель
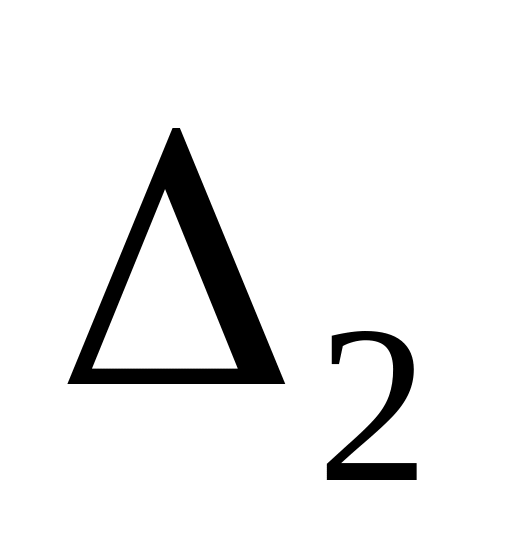 ,
заменив в определителе
второй столбец, столбцом свободных
членов:
,
заменив в определителе
второй столбец, столбцом свободных
членов:
 .
.Найдем определитель
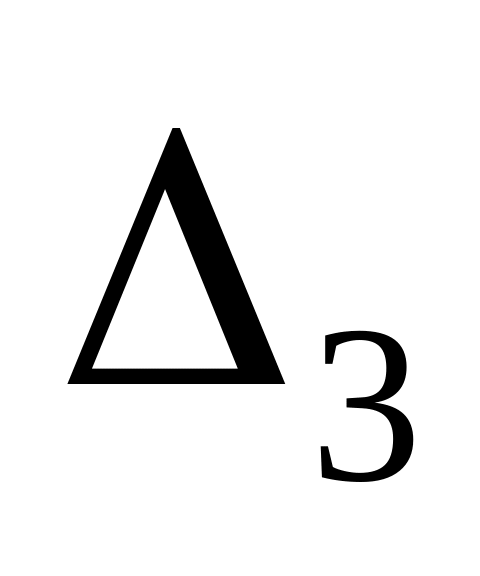 ,
заменив в определителе
третий столбец, столбцом свободных
членов:
,
заменив в определителе
третий столбец, столбцом свободных
членов:
 .
.Найдем решения системы, воспользовавшись формулами Крамера (4.4):
![]() ;
;
![]() ;
;
![]() .
.
Ответ: (1, -1, 2).
Пример 4. Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент (свой для каждого банка). В начале года 1/3 вклада, который составляет 600 ден. ед. , вложили в первый банк, а оставшуюся часть вклада во второй банк. К концу года сумма этих вкладов стала равна 700 ден. ед. Если бы первоначально 1/3 вклада положили во второй банк, а оставшуюся часть вклада - в первый банк, то к концу
года сумма этих вкладов стала бы равна 680 ден. ед. .а) Записать в математической форме условия вложения денег. б) Какой процент начисляет каждый банк?
Решение.
Пусть x![]() – процентная ставка начисления I-го
банка, x
– процентная ставка начисления I-го
банка, x![]() – процентная ставка начисления II-го
банка. Тогда
– процентная ставка начисления II-го
банка. Тогда
![]() вклада в I банк
составит:
вклада в I банк
составит:
![]() д.е.
д.е.
![]() вклада в I банк
составит:
вклада в I банк
составит:
![]() д.е.
д.е.
Так как к концу года суммы этих вкладов составили 700 д.е. в I-м банке и 680 д.е. во 2-м банке. Составим систему уравнений:
![]() .
.
Решим систему по формулам Крамера:
![]()
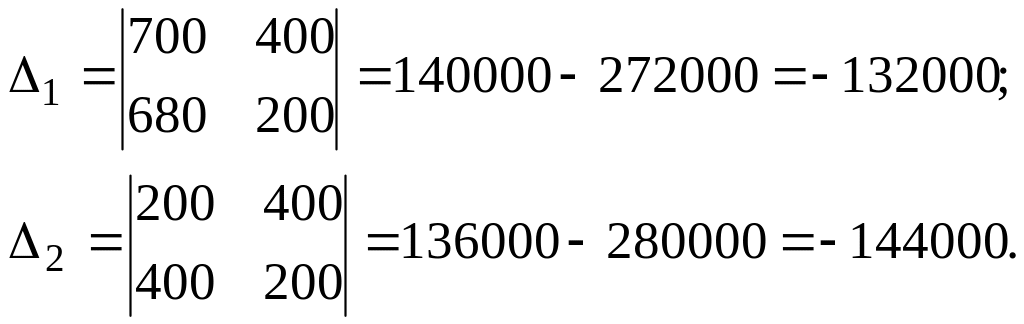
Тогда

Таким образом, процентная ставка I-го банка составляет 10% и II-го банка 20%.
Пример 5. В таблице приведены данные об исполнении баланса за отчетный период.
-
отрасль
потребление
конечный продукт
валовый выпуск
энергетика
машино-
строение
производство
энергетика
машиностроение
7
12
21
15
72
123
100
150
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроения сохранится на прежнем уровне.
Решение. По условию имеем вектор конечного продукта
![]()
Валовый выпуск: x1=100; x2=150.
Объем продукции: x11=7; x12=21;
x21=12; x22=15.
По
формуле
![]() ,
находим
,
находим
![]()
![]()
![]()
![]()
Т.е. матрица прямых затрат примет вид
![]() ,
,
которая имеет неотрицательные элементы и удовлетворяет критерию продуктивности:
![]() .
.
Необходимый объем валового выпуска X найдем по формуле: X = ( E – A )-1Y.
Найдем матрицу полных затрат
![]()
Т.к.
![]()
то
![]() ,
,
![]() ,
,
тогда
![]() .
.
Т.е. валовый выпуск в энергетической отрасли надо увеличить до 179 усл.ед., а в машиностроительной – до 160.5 усл.ед..
