
- •Задачник-практикум по линейной алгебре
- •Часть I.
- •6.1. Краткие теоретические сведения 54
- •Тема 1. Матрицы. Операции над матрицами
- •1.1. Краткие теоретические сведения
- •1.2. Пример выполнения заданий практической части
- •1.3. Задания для аудиторного занятия
- •1.4. Домашнее задание
- •Тема 2. Определители n-го порядка. Методы вычисления определителей n-го порядка
- •2.1. Краткие теоретические сведения
- •1. Вычисление определителей второго порядка по определению.
- •2. Вычисление определителей третьего порядка по определению (правило треугольника).
- •3. Приведение определителя к треугольному виду.
- •4. Разложение определителя по элементам некоторых строк (столбцов).
- •5. Метод понижения порядка определителя.
- •2.2 . Пример выполнения заданий практической части
- •2.3. Задания для аудиторного занятия
- •2.4. Домашнее задание
- •Тема 3. Нахождение обратных матриц. Решение матричных уравнений.
- •3.1. Краткие теоретические сведения
- •3.2. Пример выполнения заданий практической части
- •3.3. Задания для аудиторного занятия
- •3.4. Домашнее задание
- •Тема 4. Ранг матрицы
- •4.1. Краткие теоретические сведения
- •4.2. Пример выполнения заданий практической части
- •5.2. Пример выполнения заданий практической части
- •5.3. Задания для аудиторного занятия
- •5.4. Домашнее задание
- •Тема 6. Решение систем линейных уравнений методом Гаусса. Фундаментальная система решений
- •6.1. Краткие теоретические сведения
- •6.2. Пример выполнения заданий практической части
- •6.3. Задания для аудиторного занятия
- •6.4. Домашнее задание
Тема 4. Ранг матрицы
4.1. Краткие теоретические сведения
Определение. Рангом матрицы называют максимальное числу ее линейно независимых строк (столбцов). Обозначение: rangA или r(A).
Свойства ранга:
1. Ранг нулевой матрицы считается равным нулю.
2.
![]() .
.
3.
![]() у матрицы
у матрицы
![]() -го
порядка тогда и только тогда, когда
-го
порядка тогда и только тогда, когда
![]() .
.
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований.
Теорема
о ранге матрицы: Рангом матрицы
![]() равен наивысшему порядку отличных от
нуля миноров этой матрицы.
равен наивысшему порядку отличных от
нуля миноров этой матрицы.
Алгоритм №1 вычисления ранга матрицы
(метод окаймления миноров).
1) Если все элементы матрицы равны 0, то rang A=0. Если в матрице есть элементы, отличные от 0, то вычисляем миноры 2-го порядка.
2) Если все миноры 2-го порядка равны 0, то rang A=1. Если нашелся минор 2-го порядка, отличный от 0, то вычисляем миноры 3-го порядка, окаймляющие найденный ненулевой минор 2-го порядка.
3) Если все миноры 3-го порядка равны 0, то rang A=2. Если найдется минор 3-го порядка, отличный от 0, то вычисляем миноры 4-го порядка,
окаймляющие найденный ненулевой минор 3-го порядка и т.д.
4) Если найден минор k-го порядка, отличный от нуля, а все миноры (k+1)-го порядка, окаймляющие найденный ненулевой минор k-го порядка, равны нулю, то ранг матрицы равен k.
Определение. Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число,
4) транспонирование матрицы,
5) отбрасывание нулевой строки (столбца).
Теорема. Элементарные преобразования не меняют ранга матрицы.
Определение. Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны.
Если матрицы А и В эквивалентны, то это записывается так: A ~B.
Алгоритм №2 вычисления ранга матрицы
(метод элементарных преобразований).
1. С помощью элементарных преобразований получить а11=1.
2. С помощью элементарных преобразований получить аi1=0, i1 ( все элементы первого столбца, кроме первого, равны 0).
3. Выполнить пункты 1 и 2 алгоритма для элементов второго столбца.
4. продолжать алгоритм до тех пор, пока матрица не будет приведена к ступенчатому виду:
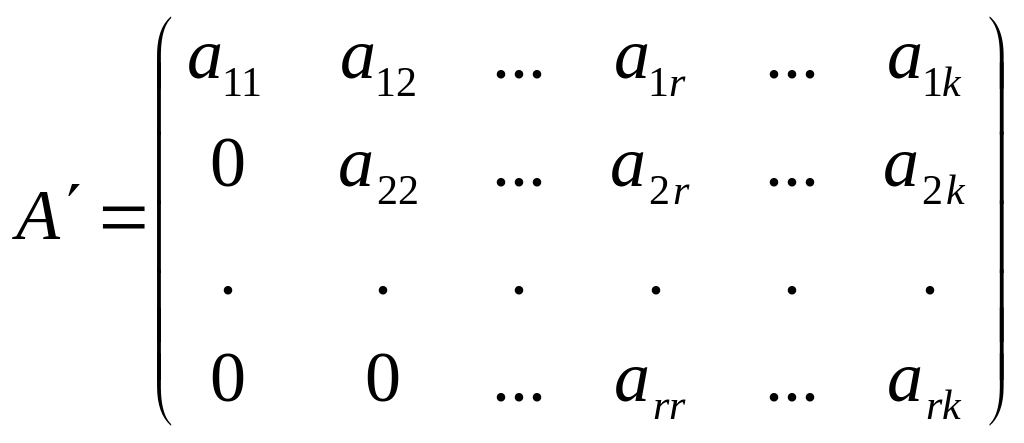 .
.
5.
Ранг полученной ступенчатой матрицы
А
будет равен рангу исходной матрицы.
rangA
= rangA
=
![]() .
.
Строки
(столбцы) матрицы
![]() называются линейно
зависимыми,
если существуют такие числа
называются линейно
зависимыми,
если существуют такие числа
![]() не равные одновременно нулю, что линейная
комбинация строк матрицы равна нулевой
строке:
не равные одновременно нулю, что линейная
комбинация строк матрицы равна нулевой
строке:
![]() ,
где
,
где
![]() .
В противном случае строки матрицы
называются линейно
независимыми.
.
В противном случае строки матрицы
называются линейно
независимыми.
4.2. Пример выполнения заданий практической части
Пример 1. Найти методом окаймления миноров ранг матрицы
 .
.
Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор
![]() .
.
Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:
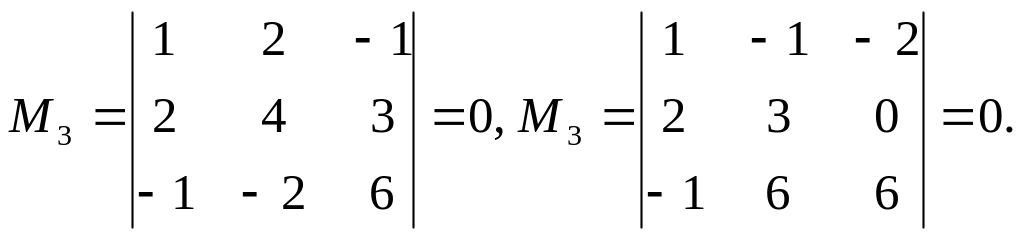
Таким
образом, все окаймляющие миноры третьего
порядка оказались равными нулю. Ранг
матрицы А равен двум:
![]() .
.
Пример 2. Найти ранг матрицы с помощью элементарных преобразований:
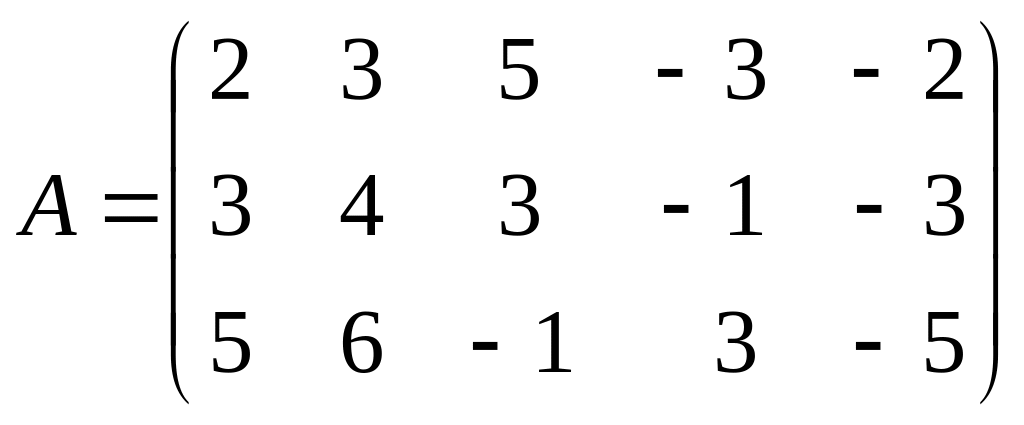 .
.
Решение. Из второй строки вычтем первую и переставим эти строки
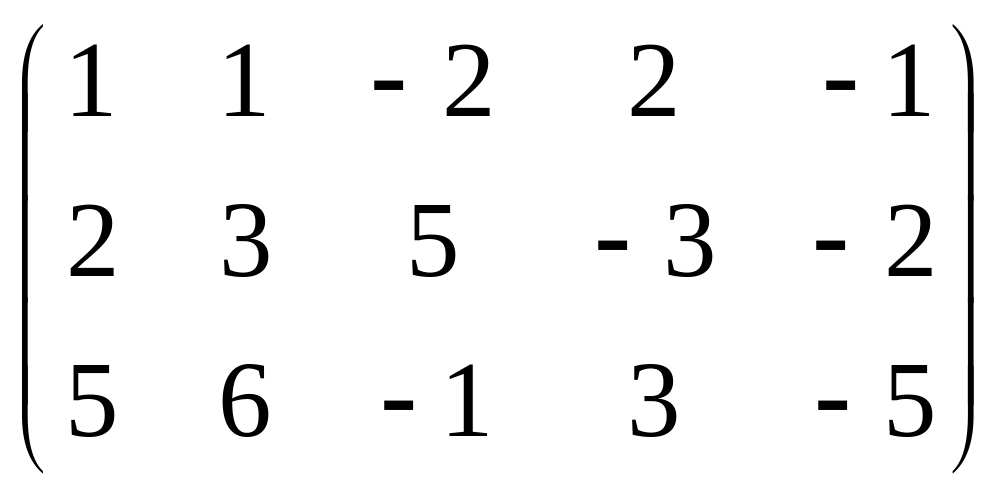 .
.
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
 ;
;
из третьей строки вычтем первую, получим матрицу
 ,
,
которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2.
Пример
3. Выяснить, при каком значении
параметра
![]() матрица имеет 3 линейно независимые
строки:
матрица имеет 3 линейно независимые
строки:
 .
.
Решение.
Матрица
![]() имеет три линейно независимые строки,
если ее ранг равен 3, т.е.
.
Вычислим определитель матрицы:
имеет три линейно независимые строки,
если ее ранг равен 3, т.е.
.
Вычислим определитель матрицы:
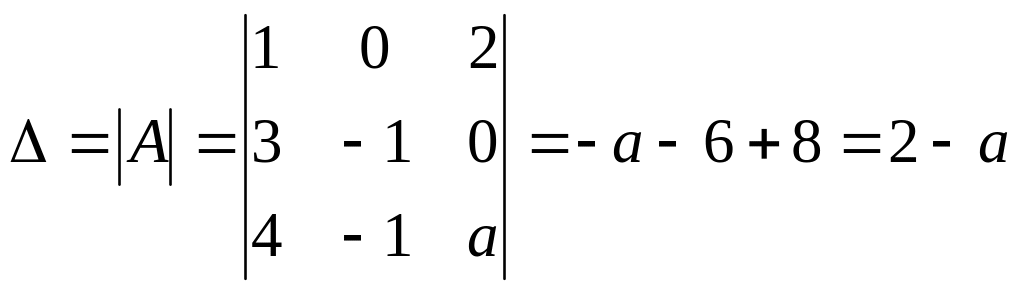 ,
,
![]() ,
т.е.
,
т.е.
![]() ;
;
![]() .
.
Следовательно,
при всех значениях
,
кроме
![]() ,
все строки линейно независимы.
,
все строки линейно независимы.
Пример
4. Определить максимальное число
линейно независимых строк (столбцов)
матрицы:
 .
.
Решение. С помощью элементарных преобразований, не меняющих ранга матрицы, приведем ее к ступенчатому виду:
 ~
~
Значит,
ранг матрицы
![]() и исходная матрица имеет 3 линейно
независимые строки (или столбца).
и исходная матрица имеет 3 линейно
независимые строки (или столбца).
4.3. Задания для аудиторного занятия
1. Найти методом окаймления миноров ранг матрицы:
1.1.
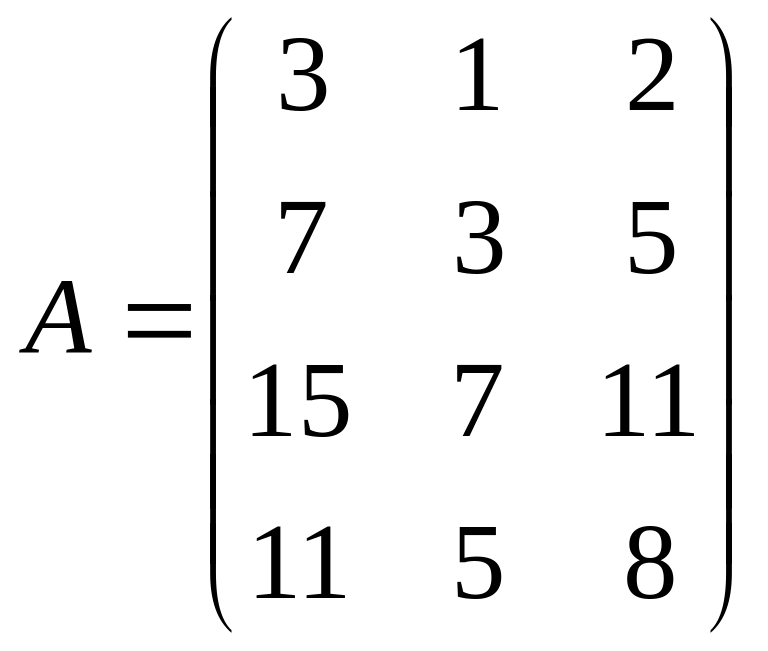 ; 1.2.
; 1.2.
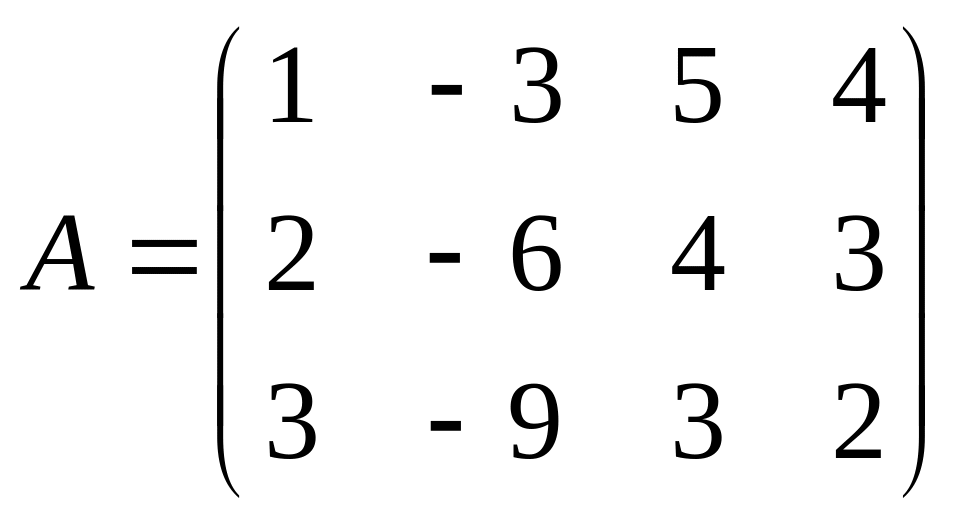 ;
;
1.3.
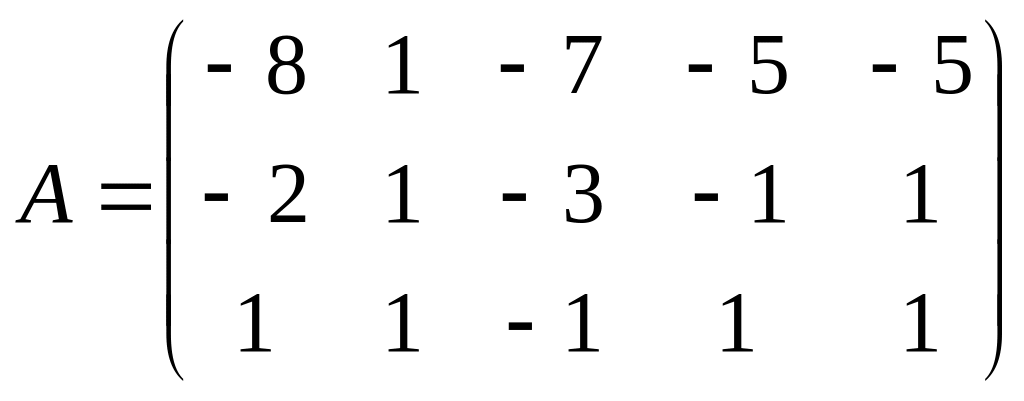 ; 1.4.
; 1.4.
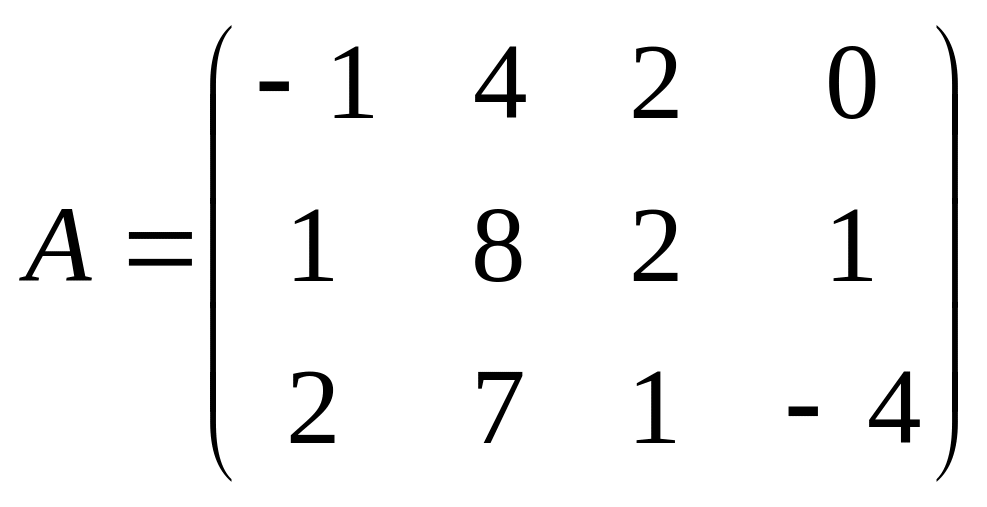 .
.
2. Найти ранг матрицы с помощью элементарных преобразований:
2.1.
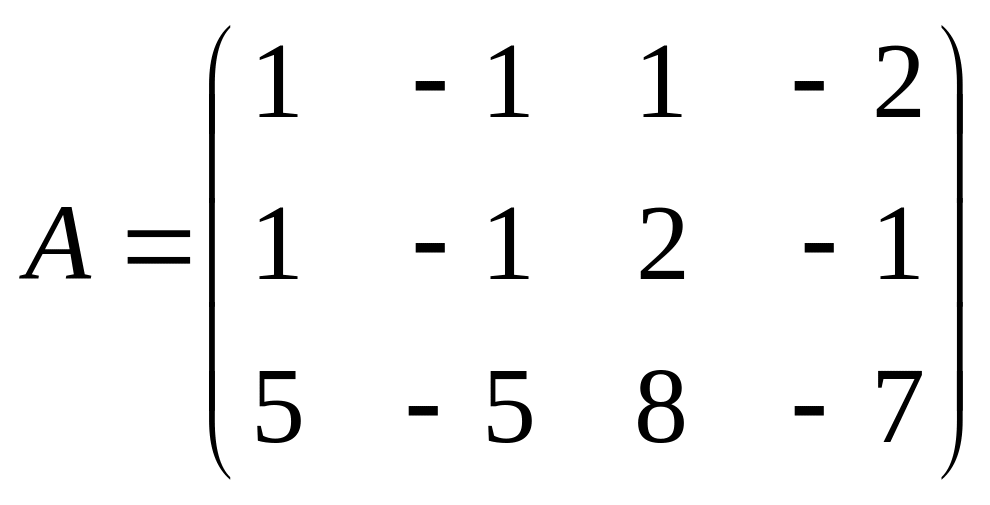 ;
2.2.
;
2.2.
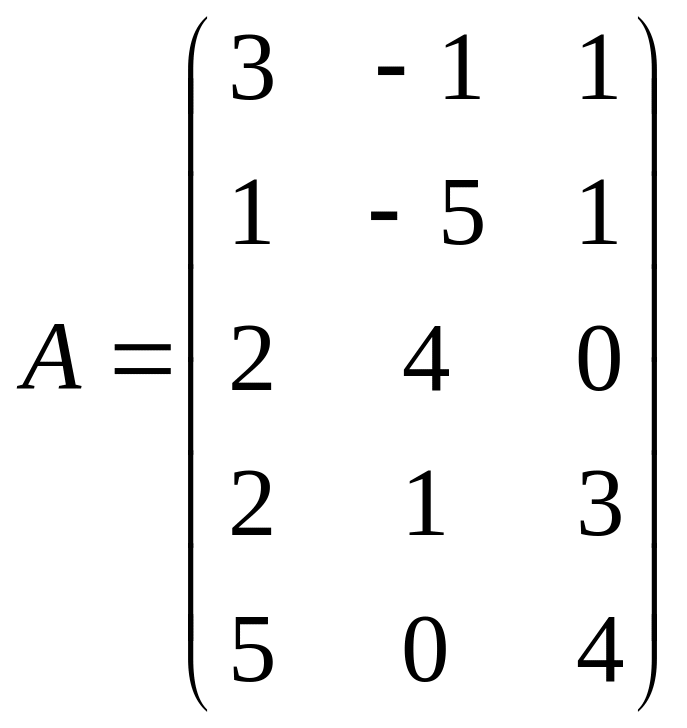 ;
;
2.3.
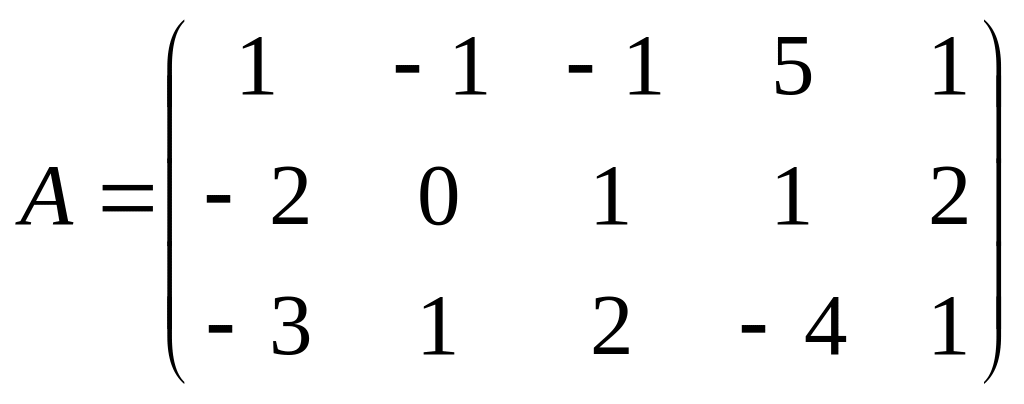 ;
2.4.
;
2.4.
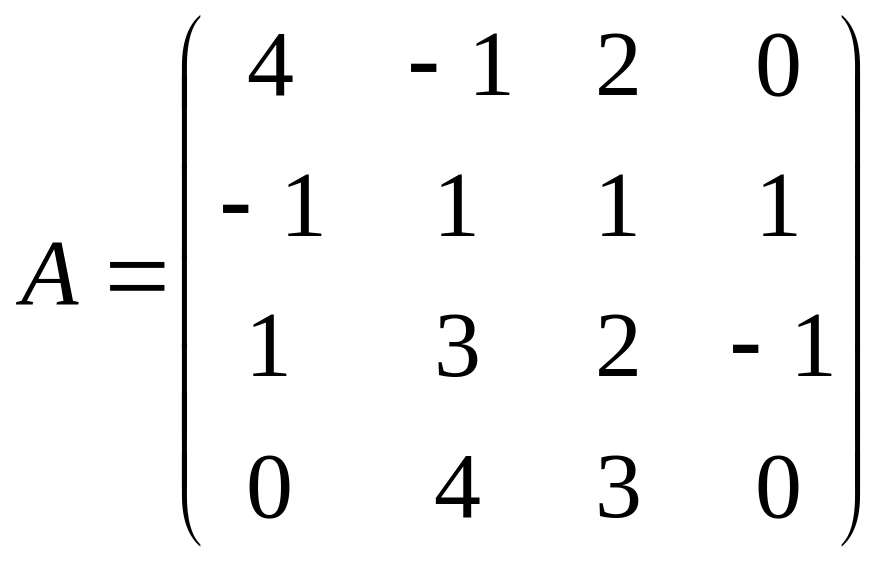 ;
;
2.5.
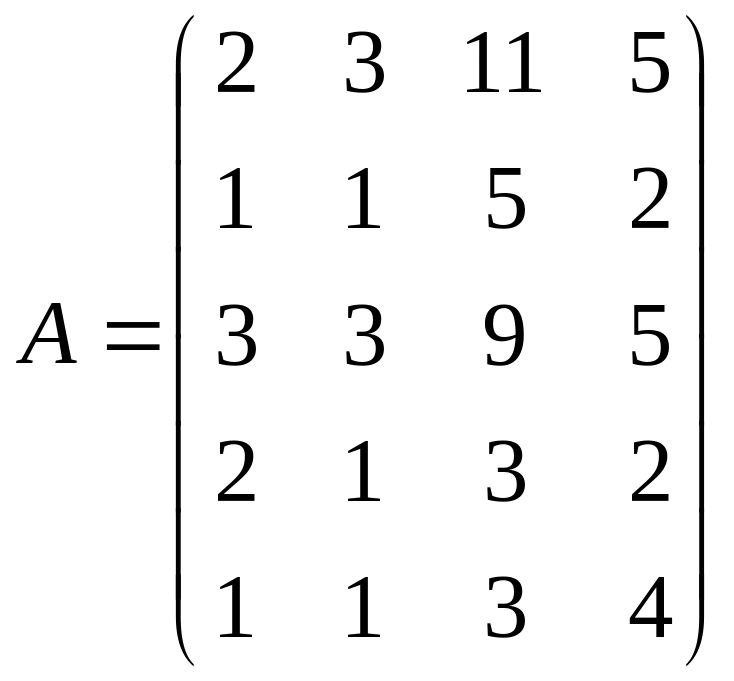 ;
2.6.
;
2.6.
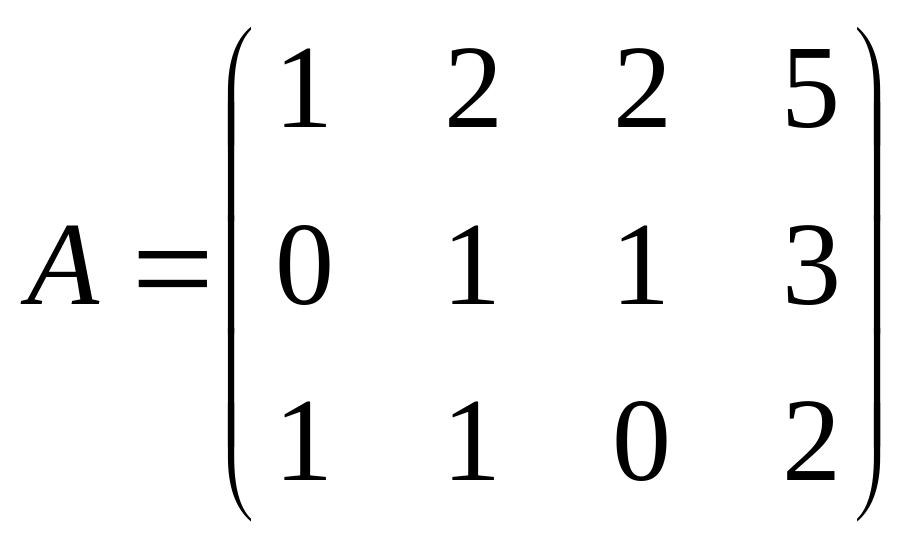 .
.
3. Найти максимальное число линейно независимых строк матриц:
3.1.
 ;
3.2.
;
3.2.
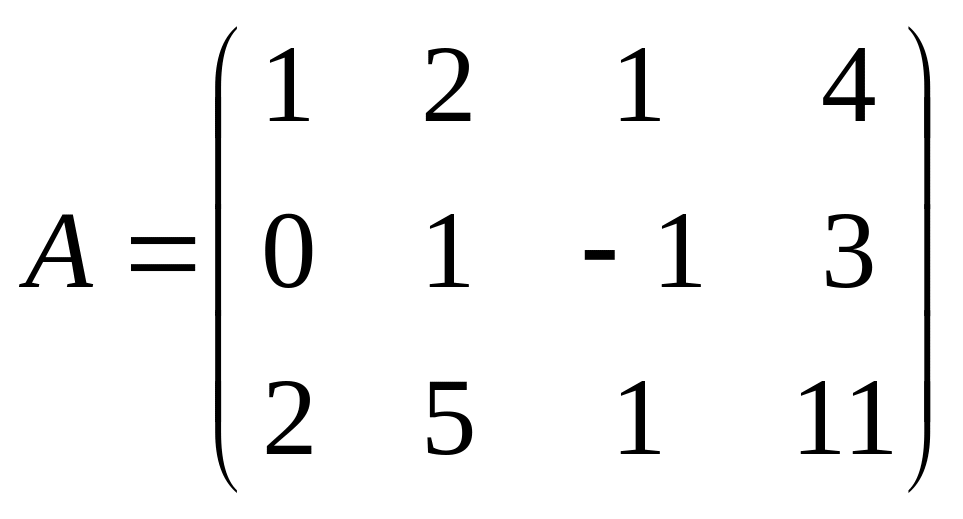 ;
;
3.3.
 ;
3.4.
;
3.4.
 .
.
4.4. Домашнее задание
1. Найти методом окаймления миноров ранг матрицы:
1.1.
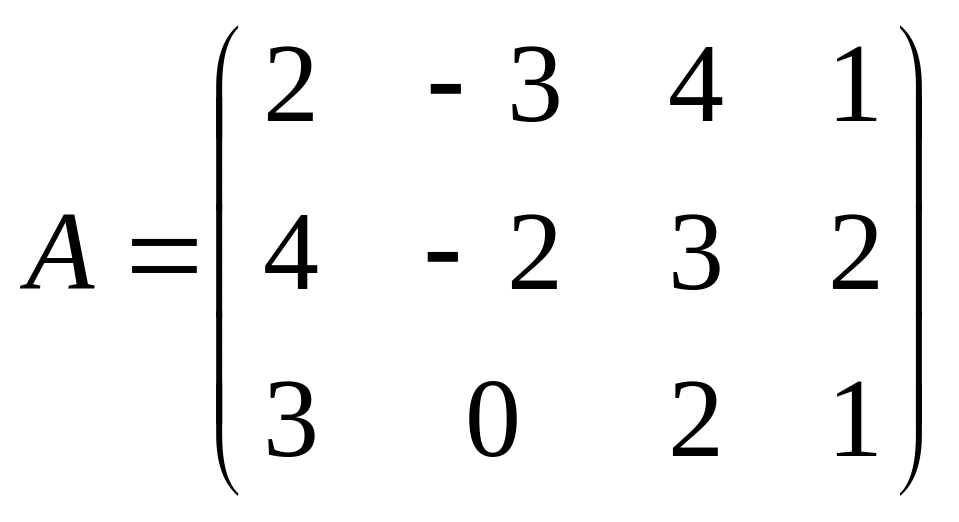 ;
1.2.
;
1.2.
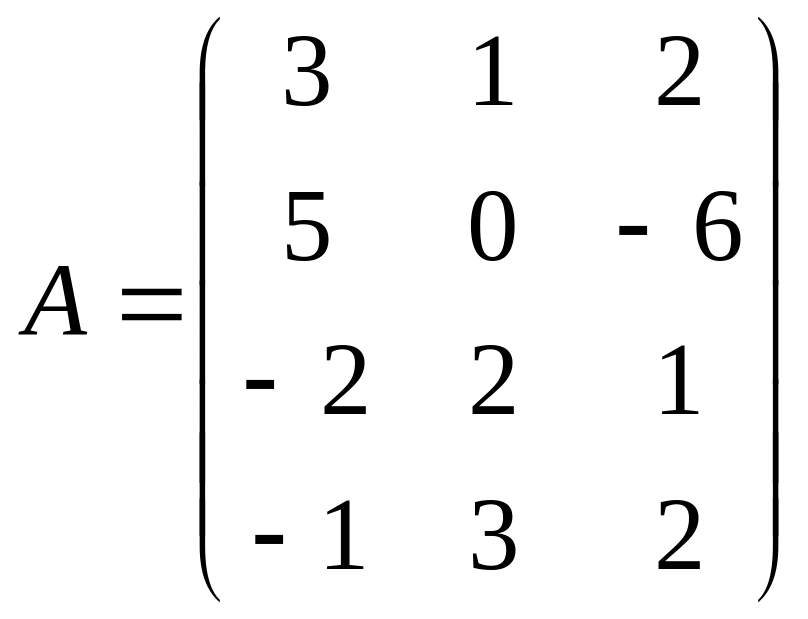 ;
;
1.3.
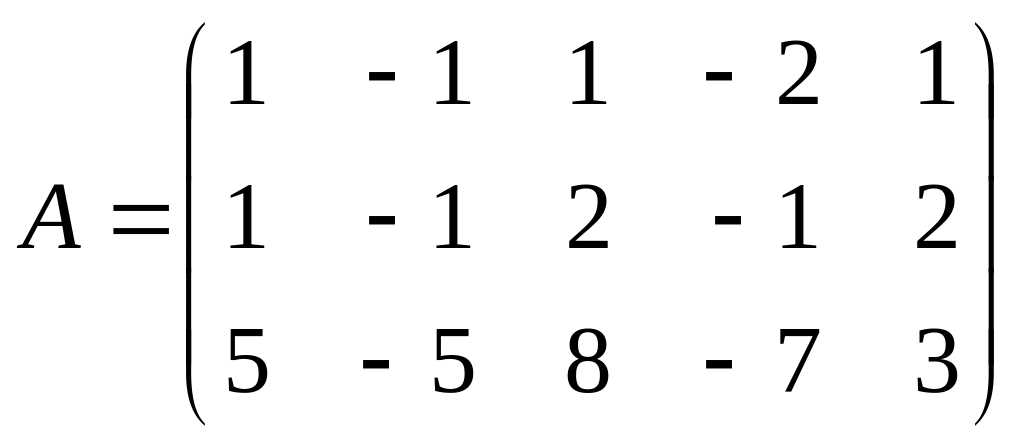 .
.
2. Найти ранг матрицы с помощью элементарных преобразований:
2.1.
 ;
2.2.
;
2.2.
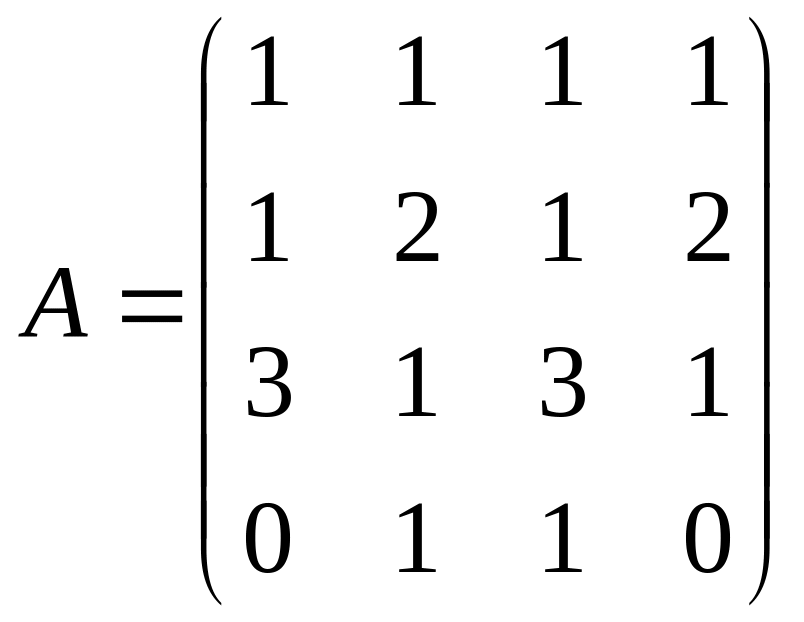 ;
;
2.3.
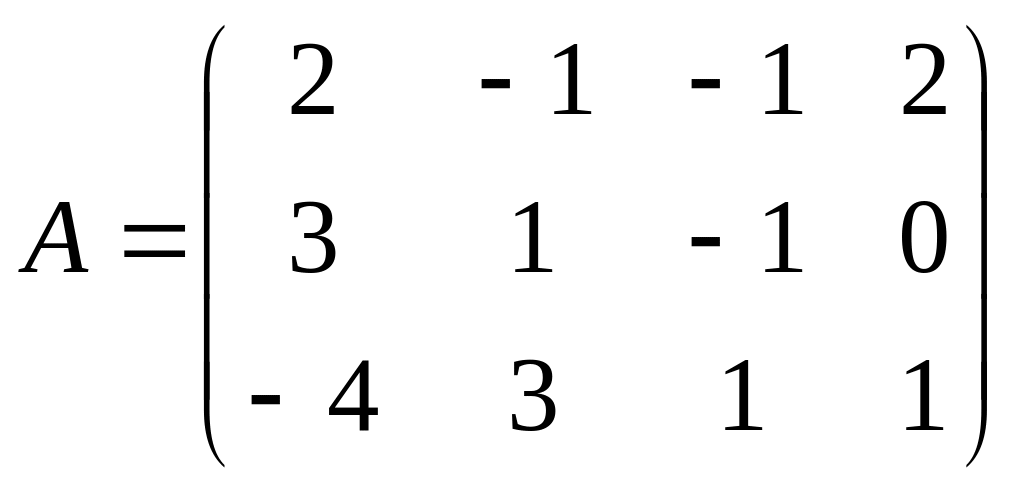 .
.
3. Найти максимальное число линейно независимых столбцов матриц:
3.1.
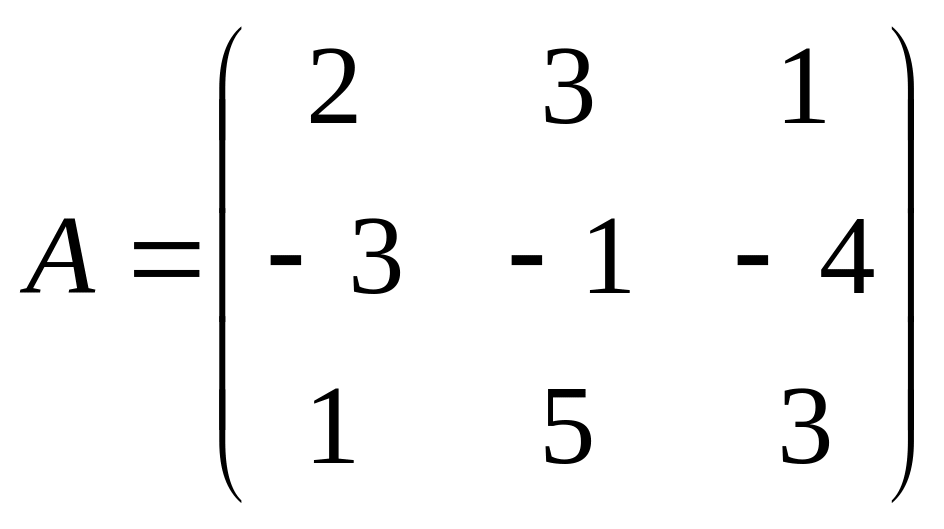 ;
3.2.
;
3.2.
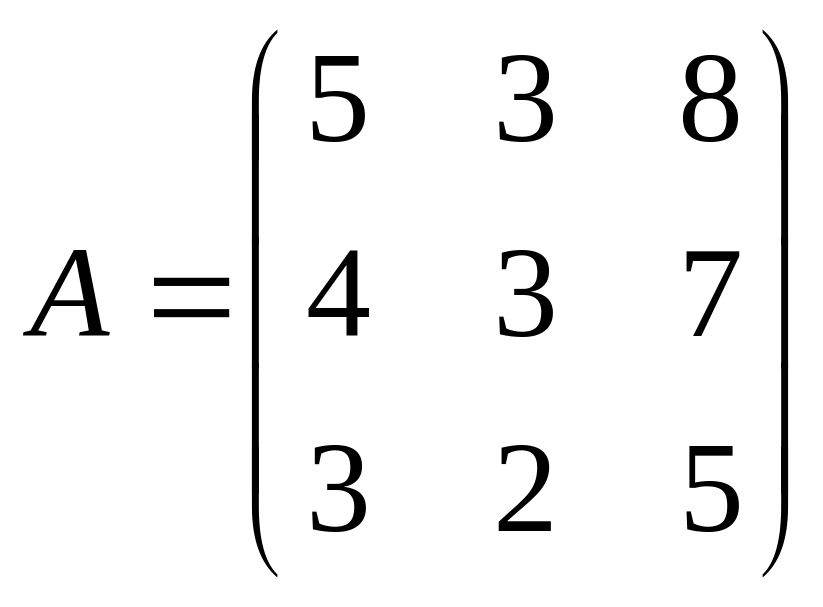 .
.
Тема 5. Решение систем линейных уравнений: матричный способ, формулы Крамера. Теорема Кронекера-Капелли: исследование числа решений систем
5.1. Краткие теоретические сведения
Пусть дана система n линейных уравнений с n неизвестными, причем определитель системы отличен от 0.
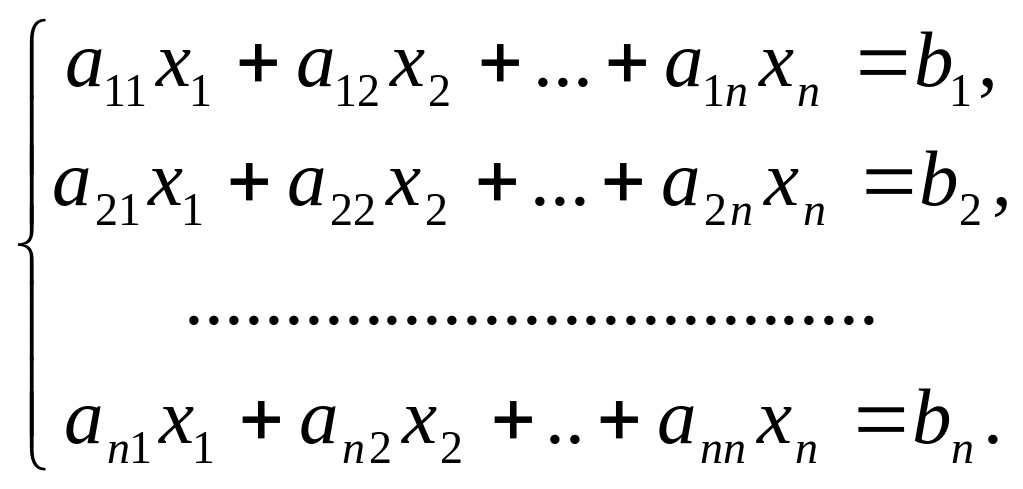 (5.1)
(5.1)
Перепишем эту систему в матричной форме, если
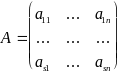 ;
;
 ;
;
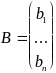

тогда систему (5.1) можно записать в матричном виде, то есть AX=B . (5.2)
Упорядоченная совокупность n вещественных чисел (c1, c2,..., cn) называется решением системы (5.1), если в результате подстановки этих чисел вместо соответствующих переменных x1, x2,..., xn каждое уравнение системы обратится в тождество; другими словами, если существует вектор C= (c1, c2,..., cn)T такой, что AC≡B.
Система (5.1) называется совместной, если она имеет, по крайней мере, одно решение. Система называется несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Две системы уравнений называются равносильными (эквивалентными), если они имеют одно и тоже множество решений.
Вопрос о совместности системы (5.1) решается следующей теоремой.
Теорема
(Кронекера-Капелли): Система
линейных уравнений совместна тогда и
только тогда, когда ранги матриц A и
расширенной матрицы
![]() совпадают, т.е.
совпадают, т.е.
r(A) = r( ) = r.
Если ранг матрицы совместной системы равен числу переменных r=n, то система (5.1) имеет единственное решение. Если ранг матрицы совместной системы меньше числа переменных r<n, то система (5.1) неопределенная и имеет бесконечное множество решений.
Так как матрица А невырожденная, тогда данное матричное уравнение (5.2) имеет решение, которое можно найти по формуле: -1 . (5.3)
Отыскание решения системы по формуле (5.3) называют матричным способом решения системы, или решением по методу обратной матрицы.
Любой элемент матрицы столбца, стоящей в правой части формулы (5.3) имеет вид
![]() ,
где
,
где
![]() -
алгебраическое дополнение к соответствующему
элементу матрицы А,
-
алгебраическое дополнение к соответствующему
элементу матрицы А,
– определитель матрицы А.
Получим формулы, которые называют формулами Крамера:
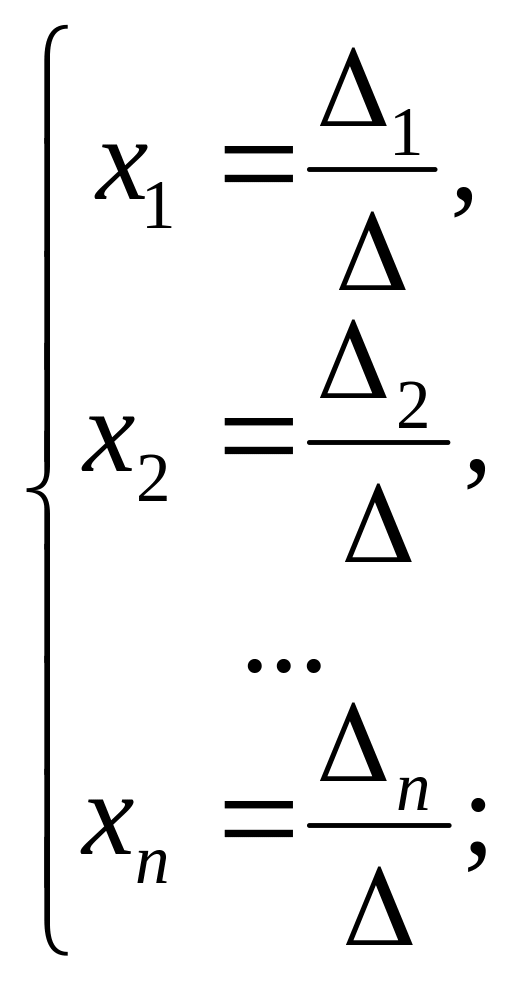 (5.4)
(5.4)
![]() ,
где
,
где
![]() – определитель,
полученный из определителя
заменой i-го столбца
столбцом свободных членов.
– определитель,
полученный из определителя
заменой i-го столбца
столбцом свободных членов.
Модель Леонтьева многоотраслевой экономики.
Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. Американским экономистом В.Леонтьевым.
Введем следующие обозначения:
xi – общий объем продукции i-й отрасли (валовый выпуск);
xij – объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства;
yi – объем конечного продукта i-й отрасли для непроизводственного потребления.
Т.к. валовый объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то
![]() ,
i=1;2;…;n
(5.5)
,
i=1;2;…;n
(5.5)
Уравнения (5.5) называются соотношениями баланса. Введем коэффициенты прямых затрат
![]() ,
i,j
= 1;2;…n
(5.6)
,
i,j
= 1;2;…n
(5.6)
показывающие затраты продукции i-й отрасли на производство единицы продукции j-й отрасли.
Тогда соотношения баланса (5.5) примут вид
xi=![]() i=1;2;…n
(5.7)
i=1;2;…n
(5.7)
Обозначим:

где X - вектор валового выпуска, Y- вектор конечного продукта, A - матрица прямых затрат.
Тогда (5.7) можно записать в матричном виде
X = AX + Y. (5.8)
Соотношение (5.8) называют уравнением линейного межотраслевого баланса. Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X , который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.
Перепишем систему (5.8) с использованием единичной матрицы Е в виде
( E – A )X = Y. (5.9)
Если матрица (Е – А) невырожденная, то существует обратная матрица ( Е – А )-1 и тогда существует единственное решение (5.8)
X = ( E – A )-1Y. (5.10)
Матрица ( Е –А )-1 называется матрицей полных затрат.
Матрица А≥0 называется продуктивной, если для любого вектора Y≥0 существует решение X≥0 уравнения (5.8).
Существует несколько критериев продуктивности матрицы А:
1. Матрица А продуктивна тогда и только тогда, когда матрица ( Е –А )-1 существует и ее элементы неотрицательны.
2. Матрица А с неотрицательными элементами продуктивна, если максимум сумм элементов по любому ее столбцу (строке) не превосходит единицы, причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.
