2.3. Задания для аудиторного занятия

1. Вычислить определители с помощью правила треугольников:

1.1. ; 1.2. .

2. Решить уравнения:

2.1. 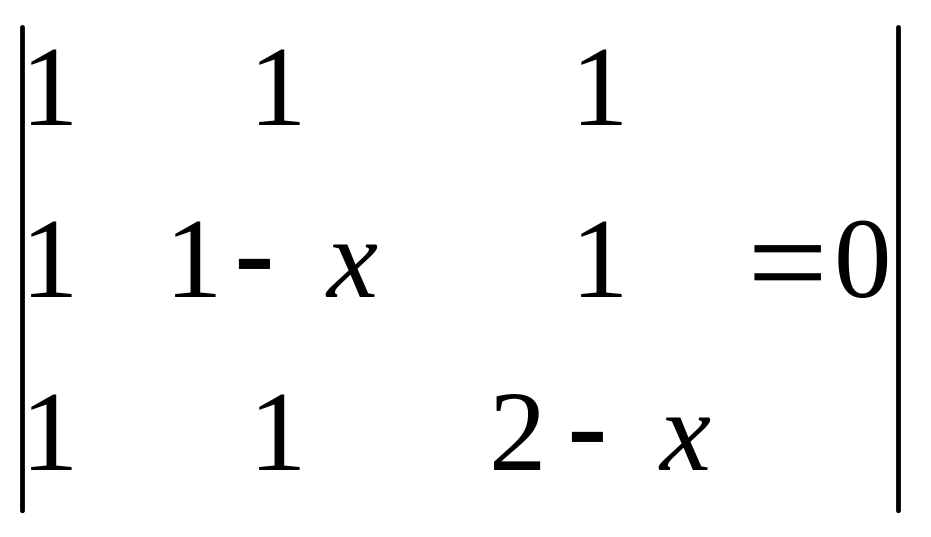; 2.2. .

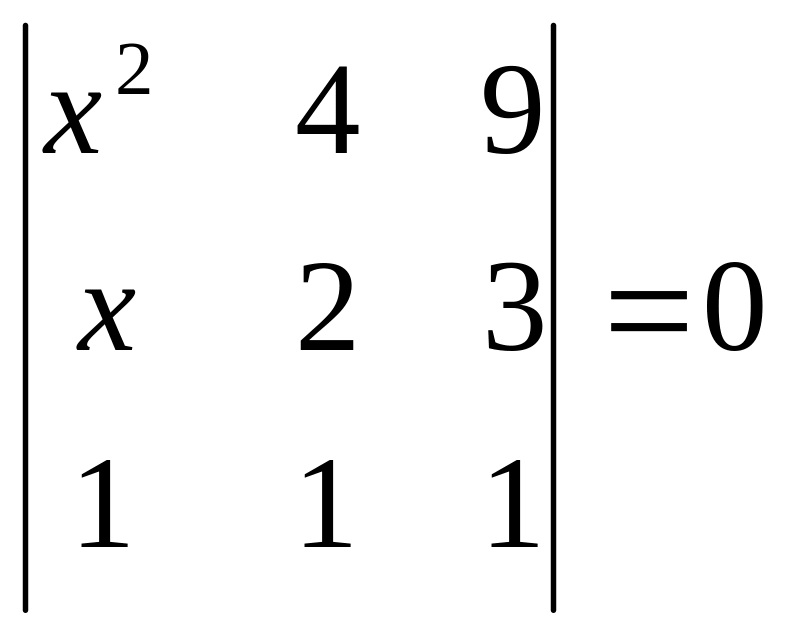3. Вычислить определитель, разложив его по элементам:

3.1. 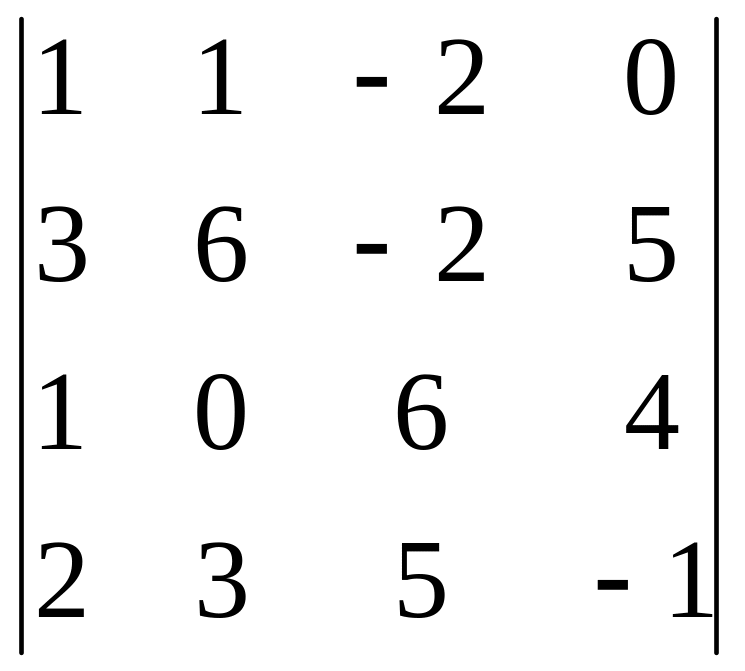4-го столбца; 3.2. 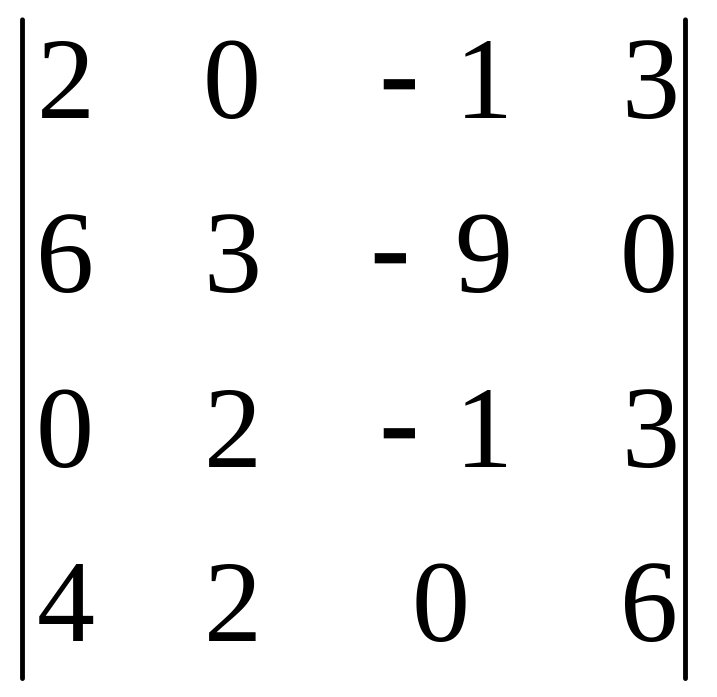3-ей строки.

4. Вычислить определители методом приведения к треугольному виду:

4.1. 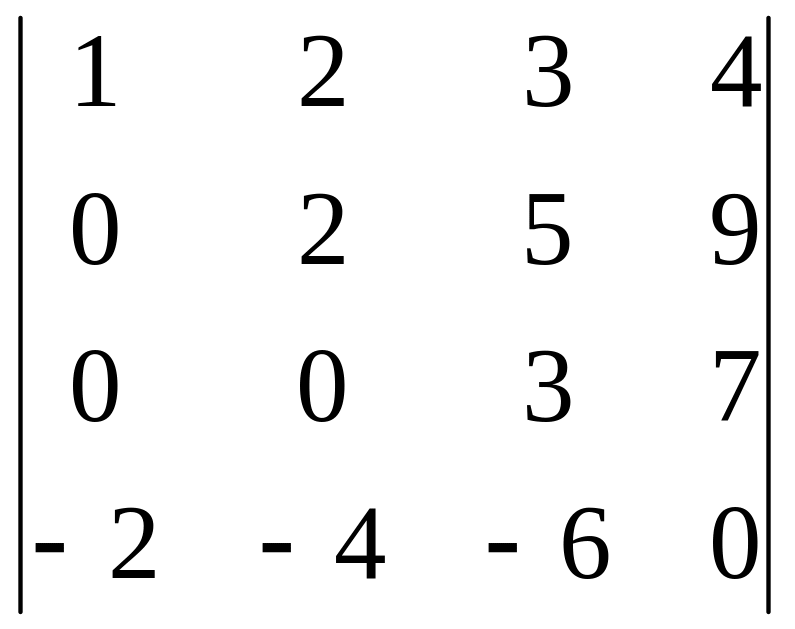; 4.2. .

5. Вычислить определители:

5.1. ; 5.2.

5.3. .

2.4. Домашнее задание

1. Вычислить определители с помощью правила треугольников:

1.1. 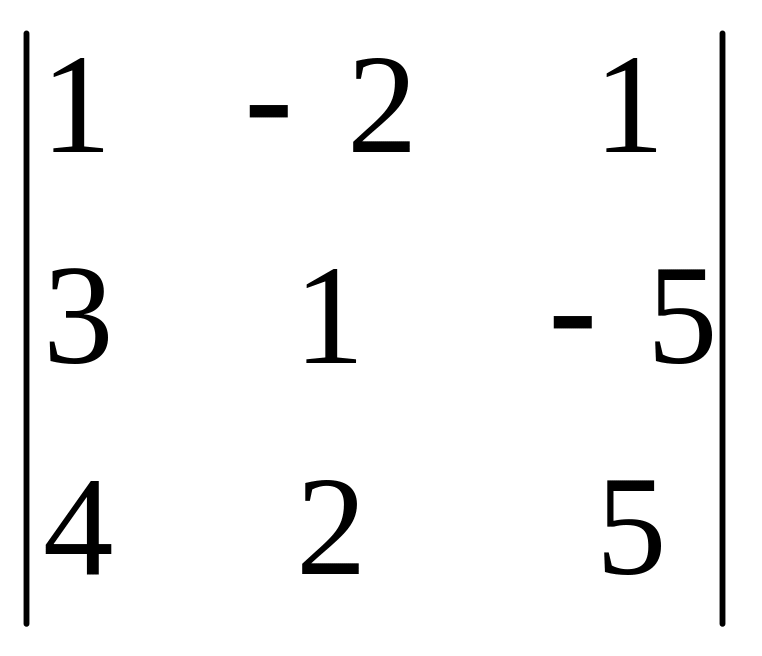; 1.2. .

2. Вычислить определитель, разложив его по элементам:

2.1. 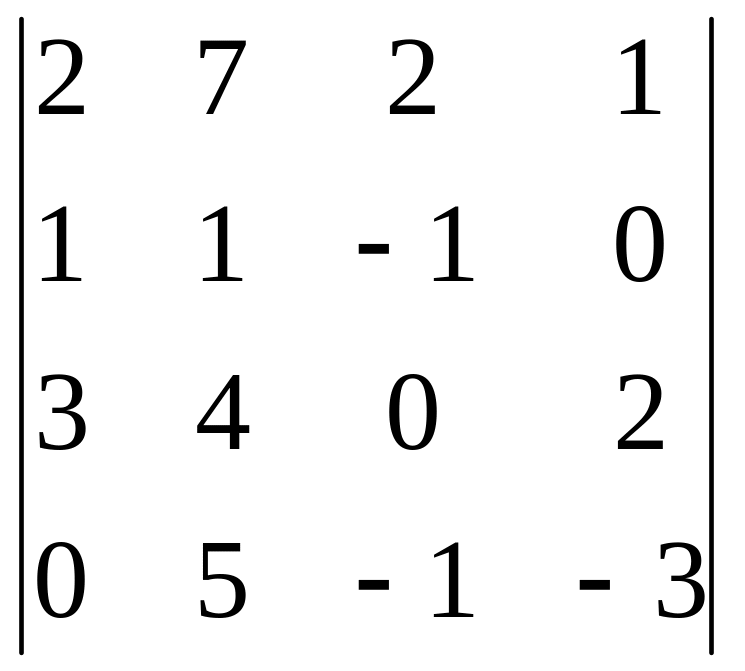4-ой строки; 2.2. 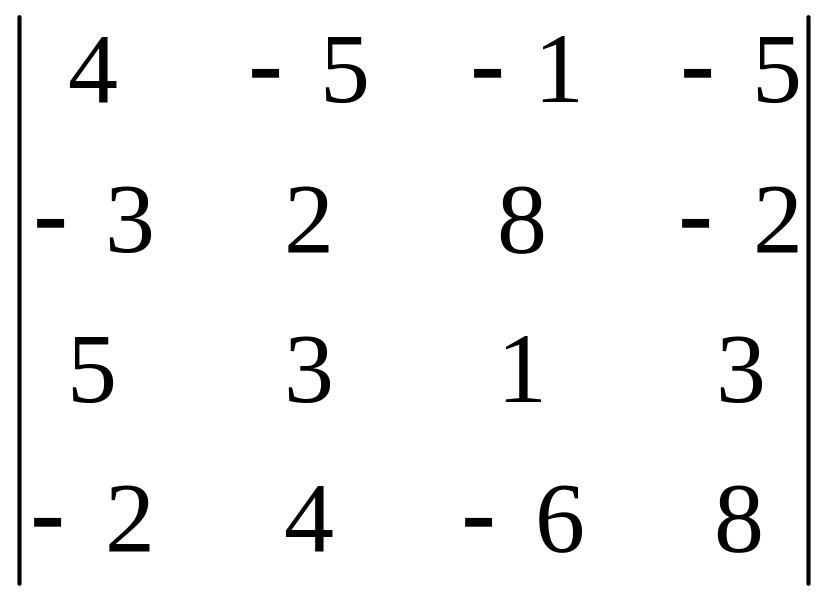3-его столбца.

3. Вычислить определители:

3.1. ; 3.2. ;

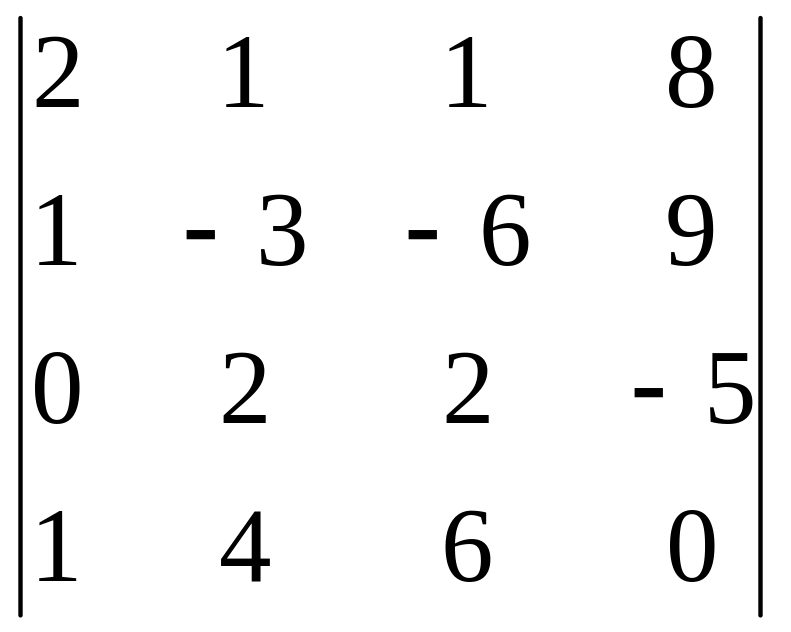3.3.

Тема 3. Нахождение обратных матриц. Решение матричных уравнений.

3.1. Краткие теоретические сведения

Определение. Квадратная матрица, определитель которой отличен от 0, называется невырожденной. Квадратная матрица, определитель которой равен 0, называется вырожденной.

Свойство 1. Вырожденная матрица не обратима.

Свойство 2. Произведение невырожденных матриц есть невырожденная матрица.

Свойство 3. Для каждой невырожденной квадратной матрицы А порядка n существует квадратная матрица А^-1, такая что АА^-1= А^-1А =Е, где Е – единичная матрица.

Определение. Квадратная матрица А^-1, такая что АА^-1= А^-1А =Е, где Е – единичная матрица, называемая обратной матрице А.

Основные свойства обратной матрицы.

1. (А^-1)^-1=А

2. (А^-1)=(А)^-1

3. (АВ)^-1=В^-1А^-1

4. 

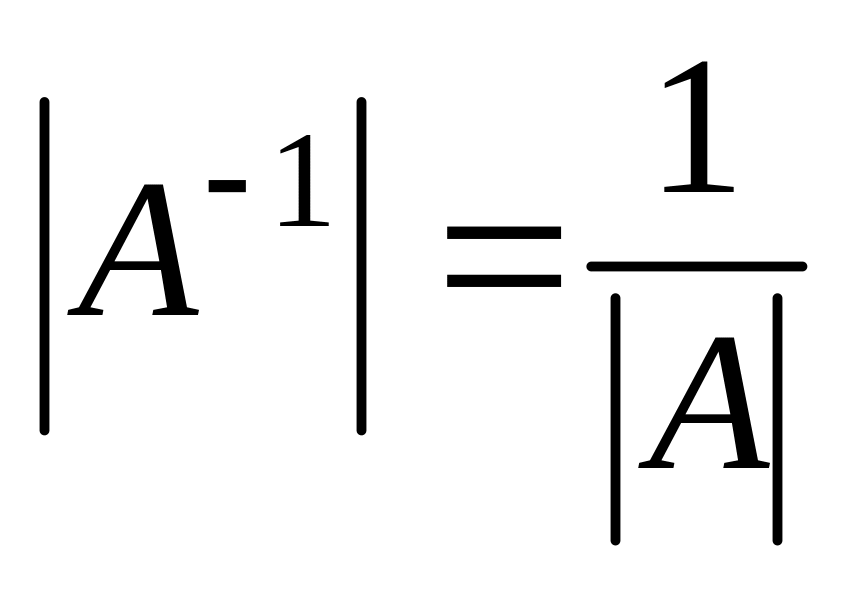
5. Е^-1=Е

Основные алгоритмы вычисления обратной матрицы.

Алгоритм №1 вычисления обратной матрицы:

1. Вычислить определитель матрицы ½A½=D;

2. Найти алгебраические дополнения ко всем элементам матрицы;

3. Все элементы матрицы заменить их алгебраическими дополнениями;

4. Транспонировать полученную матрицу;

5. Разделить все элементы матрицы на D;

6. Полученная на этапе 5 матрица и есть матрица А^-1, обратная матрице А.

Определение. Под элементарными преобразованиями матриц понимаются следующие операции:

1. Умножение или деление строки (столбца) матрицы на число к0;

2. Прибавление строки (столбца), умноженной на некоторое число к0 к другой строке (столбцу); при этом изменяется та строка (столбец), к которой прибавляют, остальные строки (столбцы) не изменяются;

3. Перемена местами строк (столбцов).

Алгоритм №2 вычисления обратной матрицы:

1. Присоединить к матрице А за вертикальной чертой единичную матрицу Е того же порядка, что и А; получим новую матрицу (А|Е);

2. Применяя элементарные преобразования 1-3 над строками матрицы (А|Е) получить слева от вертикальной черты единичную матрицу Е;

3. Тогда справа от вертикальной черты получим матрицу А^-1, обратную к матрице А.

Матричные уравнения.

Определение. Матричным уравнением будем называть уравнение вида AX=B, где А и В заданные матрицы, Х – неизвестная матрица.

Если матрица А невырожденная, тогда для нее существует обратная. Умножив обе части уравнения AX=B на А^-1, получим

A^-1  (AX)=A^-1 B ^-1 ^-1   ^-1 

Покажем, что Х - решение уравнения AX=B:

A (A^-1B)= (AA^-1) B=ЕВ=В  .