2.2.Расчетно-экспериментальная часть

2.2.1.Проведение предварительного эксперимента на объекте исследования

Особенность многофакторного эксперимента (МФЭ) состоит в том, что он предусматривает одновременное варьирование многих факторов х_ij, влияющих на параметр у. Так как изменение отклика y носит случайный характер, то в каждой точке x_i приходится проводить т параллельных опытов y₁, y₂, ..., y_m.

Пусть в рассматриваемом случае число параллельных опытов в каждой строке матрицы планирования m = 3. Перед реализацией плана на объекте необходимо рандомизировать (расположить в случайном порядке) варианты варьирования факторов, т.е. с помощью таблицы равномерно распределенных случайных чисел или компьютерной программы для проведения процесса рандомизации определить последовательность реализации вариантов варьирования плана в N × m опытах, где N – число опытов в факторном пространстве.

Провести по три опыта на основном уровне эксперимента и результаты наблюдений (соответственно вариантам варьирования плана) записать в столбцы y₁, y₂, y₃ таблицы матрицы планирования (МП), а в столбце ỹ записать среднее арифметическое значение трех параллельных опытов.

Среднее арифметическое значение параллельных опытов функции отклика ỹ рассчитать по формуле 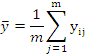(5):

(5)

где m – число параллельных опытов.

2.2.2.Проверка воспроизводимости эксперимента

Определить отклонение от среднего арифметического значения для каждого результата y_j по формуле (6) и затем по формуле (7) рассчитать оценку дисперсии. Результаты занести в таблицу МП.

∆y_j = y_jj - ỹ_j (6)

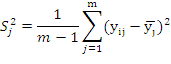(7)

Провести проверку однородности оценок дисперсий по критерию Кохрена по формуле (8), результаты занести в таблицу МП:

₍₈₎

Расчетное значение критерия Кохрена сравнивается с табличным значением G_табл – критерия, который выбирается из таблицы П.4 (приложение 4) для принятого уровня значимости q=0,05 и числа степеней свободы, соответственно: f₁=(m–1) – число степеней свободы максимальной дисперсии - числитель; f₂ = N – число степеней свободы или число опытов в факторном пространстве - знаменатель.

Гипотеза об однородности дисперсий подтверждается, если экспериментальное значение критерия Кохрена G_p не превышает табличное значение, то есть если G_табл > G_p, то опыты считаются воспроизводимыми, а оценки дисперсий s_j² - однородными.

Если данное условие не выполняется, то необходимо менять условия предварительного эксперимента, а опыты и расчеты повторить.

Если возникает предположение о наличии неоднородности дисперсий для случая, когда число повторных опытов неодинаково во всех точках, можно воспользоваться критерием Бартлета (B-критерий).

Дисперсия воспроизводимости подсчитывается по формуле 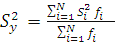(9):

(9)

2.2.3. Математическая модель объекта исследования

Расчет оценок коэффициентов уравнения регрессии производится по методу наименьших квадратов, при этом минимизируется сумма квадратов отклонений между экспериментальными значениями исследуемого параметра и значениями, вычисленными для тех же точек факторного пространства. Благодаря предварительной стандартизации масштаба факторов и ортогональности МП, расчет оценок коэффициентов регрессии в ПФЭ превращается в простую арифметическую процедуру. Коэффициенты регрессии рассчитать по формулам 10:

; ; (10)

где коэффициенты b_i характеризуют силу влияния каждого из факторов, а их знак (- или +) - направление влияния факторов. То же относится и к коэффициентам b_ij, характеризующим силу и направление влияния факторов взаимодействия.

Благодаря оптимальным свойствам плана 2^k, все коэффициенты его полиномиальной модели оцениваются независимо друг от друга с одинаковыми минимальными дисперсиями и максимальной точностью.

Уравнение регрессии, описывающее поверхность отклика трех- факторного эксперимента, имеет общий вид (11):

y = b ₀ + b ₁x₁ + b ₂x₂ + b ₃x₃ + b ₁₂x₁x₂ + b ₁₃x₁x₃+ b ₂₃x₂x₃+ b ₁₂₃ x₁x₂ x₃ (11)

Подставить рассчитанные значения коэффициентов регрессии в уравнение 11 и получить предварительное уравнение регрессии, описывающее поверхность отклика вашего объекта исследования.