
- •Электростатическая теорема Гаусса-Остроградского.
- •2. Уравнения Максвелла
- •3. Плоские электромагнитные волны в диэлектрике
- •Электромагнитная индукция
- •1. Явление электромагнитной индукции. Правило Ленца
- •2. Основной закон электромагнитной индукции
- •3. Работа в электрическом поле. Потенциальность электростатического поля
- •Телесный угол
- •Доказательство теоремы Гаусса
- •Магнитные силы. Сила Лоренца. Закон Ампера
Механика
Основные понятия классической механики. Скорость, ускорение. Угловая скорость. Угловое ускорение.
Законы Ньютона. Закон сохранения импульса. Центр масс системы частиц.
Работа силы. Мощность. Кинетическая и потенциальная энергия. Полная энергия механической системы.
Принцип относительности Эйнштейна. Преобразования Лоренца.
Лоренцево сокращение длины. Собственное время объекта. Парадокс близнецов.
Преобразование скорости в СТО.
Интервал между событиями. Принцип наименьшего действия. Функция Лагранжа в СТО.
Энергия и импульс свободной частицы.
Уравнения Максвелла. Токи смещения. Материальные уравнения.
Электромагнитные волны в диэлектрике.
Явление электромагнитной индукции. Правило Ленца. Основной закон электромагнитной индукции. Трактовка Максвелла.
Закон Кулона. Работа в электростатическом поле. Потенциальность электростатического поля. Потенциал системы точечных зарядов.
Электростатическая теорема Гаусса-Остроградского.
Закон Био- Савара-Лапласа.
Сила Лоренца. Сила Ампера.
Основные положения и понятия МКТ. Агрегатные состояния вещества.
Основное уравнение МКТ(уравнение Клаузиуса).
Уравнение Менделеева-Клапейрона. Закон Дальтона. Изопроцессы.
Средняя энергия молекул. Закон о равномерном распределении кинетической энергии по степеням свободы.
Закон Максвелла распределения молекул идеального газа по скоростям.
Барометрическая формула. Распределение Больцмана.
Явления переноса в газах. Закон Фика. Закон Фурье. Сила внутреннего трения.
Реальные газы. Уравнение Ван-дер-Ваальса.
Термодинамическая система. Равновесные и неравновесные состояния. Равновесный процесс. Внутренняя энергия, работа и теплота.
Первое начало термодинамики. Теплоёмкость и внутренняя энергия идеального газа. Уравнение Майера.
Адиабатический процесс. Работа, совершаемая идеальным газом при различных процессах.
Микросостояние и макросостояние. Статистический вес макросостояния. Энтропия. Свойства энтропии. Теорема Нернста.
Второе начало термодинамики. Проблема тепловой смерти Вселенной.
Фотоэффект. Уравнение Эйнштейна. Давление света. Вынужденное излучение. Лазеры.
Гипотеза де Бройля. Уравнение Шредингера.
Принцип суперпозиции. Физический смысл квадрата модуля пси-функции. Стандартные условия.одномерной
Квантование энергии. Энергия частицы в бесконечно глубокой
одномерной потенциальной яме. Описание физических величин в квантовой механике.
Теория Бора атома водорода. Принцип неопределённости.
Состав и характеристики атомного ядра. Ядерные силы. Энергия связи атомных ядер. Синтез легких ядер.
Радиоактивность. Закон радиоактивного распада. Ядерные реакции.
Материальной точкой называется тело, размерами которого в данной задаче можно пренебречь. Произвольное макроскопическое тело можно мысленно разбить на совокупность материальных точек. Тогда изучение движения сводится к изучению движения материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.
Абсолютно твёрдым телом наз. тело, которое не может деформироваться и при всех условиях расстояние между двумя частицами этого тела остаётся постоянным.
Абсолютно упругое тело – тело, деформация которого подчиняется закону Гука, а после прекращения действия внешних сил принимает свои первоначальные размеры.
Абсолютно неупругое тело – тело, полностью сохраняющее деформированное состояние после прекращения действия внешних сил .
 Тело
отсчёта
– произвольно выбранное тело, относительно
которого определяется положение других
движущихся или покоящихся тел.
Тело
отсчёта
– произвольно выбранное тело, относительно
которого определяется положение других
движущихся или покоящихся тел.
Система отсчёта – совокупность тела отсчёта, связанной с ним системы координат и синхронизованных между собой часов.
Уравнения движения частицы
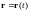 ,
,
или в компонентах

Траекторией наз. линия, описываемая движущейся частицей относительно выбранной системы отсчёта.
Траектории движений одного и того же тела в разных система отсчёта могут быть различными.
Вектор перемещения
 .
.
Скорость
 .
.
Модуль скорости
 .
.
Длина пути
 .
.
Ускорение

Полное ускорение можно представить в виде
 .
.
Тангенциальная составляющая

характеризует быстроту изменения скорости по модулю и направлена по касательной к траектории.
Нормальная составляющая

характеризует быстроту изменения скорости по направлению и направлена к центру кривизны траектории.
Вращательным движением твёрдого тела наз. движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Угловая скорость
 .
.
Вектор
 направлен вдоль оси вращения по правилу
правого винта, также как и вектор
направлен вдоль оси вращения по правилу
правого винта, также как и вектор
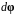 .
.
Угловое ускорение
 .
.
Имеют место формулы
 .
.
Первый закон Ньютона
Частица сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит её изменить это состояние.
Инерциальной системой отсчёта наз. система отсчёта, относительно которой свободная частица движется равномерно и прямолинейно.
Инертностью тел наз. свойство, заключающееся в том, что тела оказывают сопротивление изменению их скорости.
Инерционные и гравитационные свойства определяет масса тела.
Инертная и гравитационная массы равны друг другу.
Второй закон Ньютона

Или
 .
.
Здесь
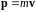
импульс.
Второй закон Ньютона справедлив только в инерциальных системах отсчёта.
Третий закон Ньютона
 .
.
Закон сохранения импульса
Импульс замкнутой системы

сохраняется. Это фундаментальный закон природы. Он является следствием однородности пространства. При параллельном переносе замкнутой системы в пространстве её физические свойства не изменяются.
Центр масс системы частиц

Центр масс системы движется как частица, в которой сосредоточена масса всей системы и на которую действует сила, равная сумме всех внешних сил, действующих на систему
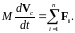
Работа силы
Элементарная работа.
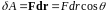 .
.
Работа
 .
.
Мощность

Кинетическая энергия
Приращение кинетической энергии частицы на элементарном перемещении равно элементарной работе на том же перемещении

Кинетическая энергия неодинакова в разных инерциальных системах отсчета.
Потенциальной энергией наз. механическая энергия системы частиц, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Потенциальным полем наз. поле, в котором работа, совершаемая силами поля при перемещении тела из одного положения в другое зависит только от начального и конечного положений.
Консервативной силой наз. сила, работа которой при перемещении частицы из одного положения в другое зависит только от начального и конечного положений частицы. Выполняются формулы

Полной энергией механической системы наз.
 .
.
Преобразования Лоренца
Инерциальная система отсчета – это такая система, в которой материальная точка, не взаимодействующая с какими-либо другими телами, движется равномерно и прямолинейно или покоится.
Принцип относительности Эйнштейна
Законы природы инвариантны (неизменны) при переходе от одной инерциальной системы отсчета к другой
Существует предельная скорость распространения взаимодействия, равная в пустоте скорости света
 см/c.
см/c.
Вообще любые взаимодействия между телами в пустоте распространяются со скоростью света.
Принцип предельной скорости выражает утверждение о том, что скорость распространения взаимодействия в пустоте носит универсальный характер и связана непосредственно со свойствами пространства и времени, а не с физической природой взаимодействия.
Пусть
имеются две системы отсчета
 и
и
 ,
причем вторая система отсчета перемещается
относительно первой в направлении их
общей оси
,
причем вторая система отсчета перемещается
относительно первой в направлении их
общей оси
 и
и
 со скоростью
со скоростью
 .
Выберем за начало отсчета времени
.
Выберем за начало отсчета времени
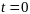 тот момент времени, в который
начала
координат совпадают.
тот момент времени, в который
начала
координат совпадают.
Пусть в момент времени из начала координат начала распространяться сферическая электромагнитная волна . В системе уравнение волнового фронта имеет вид
 .
(1)
.
(1)
Согласно принципу относительности Эйнштейна имеем в системе
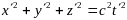 .
(2)
.
(2)
Из однородности пространства и времени вытекает требование линейности преобразования. В силу линейности преобразования
 .
(3)
.
(3)
Далее очевидно
 .
(4)
.
(4)
Формула преобразования времени в силу свойства линейности имеет вид
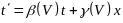 .
(5)
.
(5)
Здесь
коэффициенты
 зависят от скорости
.
Далее, очевидно, имеем
зависят от скорости
.
Далее, очевидно, имеем
 =
= .
(7)
.
(7)
Поэтому
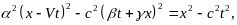 (8)
(8)
Далее
мы должны приравнять коэффициенты при
 слева к соответствующим коэффициентам
справа. Получим
слева к соответствующим коэффициентам
справа. Получим
 (9)
(9)
Решая алгебраическую систему уравнений (9), учитывая при этом принцип соответствия, получим
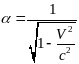 .
(10)
.
(10)
Далее находим

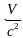 ,
(11)
,
(11)
 .
(12)
.
(12)
Итак, получили
 .
(13)
.
(13)
 (14)
(14)
 ,
(15)
,
(15)
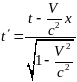 .
(16)
.
(16)
Из формул (13)-(16) можно получить формулы обратного преобразования.
Но эти формулы получаются и путем следующих рассуждений.
Системы
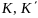 эквивалентны. Поэтому мы могли повторить
предыдущие рассуждения, взяв за исходную
систему
.
При этом должны получиться те же формулы,
но со скоростью относительного движения
эквивалентны. Поэтому мы могли повторить
предыдущие рассуждения, взяв за исходную
систему
.
При этом должны получиться те же формулы,
но со скоростью относительного движения

Формулы обратного преобразования имеют вид
 ,
(17)
,
(17)
 (18)
(18)
 ,
(19)
,
(19)
 (20)
(20)
Пространственный промежуток. Лоренцево сокращение длины.
Понятия «РАЗМЕР ТЕЛА», «промежуток времени между событиями» не имеют абсолютного характера и различны для различных систем отсчета.
Рассмотрим тонкий стержень, который покоится в системе . Его длина равна
 .
(1)
.
(1)
Измерения
координат конца масштаба в
проводятся в один и тот же момент времени
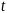 ,
что естественно, так как масштаб движется.
Имеем
,
что естественно, так как масштаб движется.
Имеем
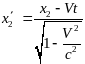 ,
(2)
,
(2)
 .
(3)
.
(3)
Отсюда получаем
 .
(4)
.
(4)
Т.о., находим
 .
(5)
.
(5)
Т.о.,
длина масштаба по отношению к системе
меньше, чем его собственная длина. Это
сокращение длины наз. лоренцевым
сокращением. Поэтому утверждение
«расстояние между двумя точками
пространства равно
 »
не имеет смысла без указания к какой
системе отсчета отнесена эта величина.
»
не имеет смысла без указания к какой
системе отсчета отнесена эта величина.
Собственное время объекта
Пусть
в
 в
системе
происходит физический процесс в
течение промежутка времени
в
системе
происходит физический процесс в
течение промежутка времени
 .
(6)
.
(6)
Тогда в системе отсчета имеем
 ,
(7)
,
(7)
 .
(8)
.
(8)
Отсюда находим
 .
(9)
.
(9)
Формула (9) была проверена экспериментально многими способами.
В
космических лучах наблюдается распад
 -
мезона и
-
мезона и
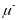 -
мезона соответственно на позитрон и
два нейтрино и на электрон и два нейтрино.
При этом наблюдается распад как
заторможенных до остановки
-
мезона соответственно на позитрон и
два нейтрино и на электрон и два нейтрино.
При этом наблюдается распад как
заторможенных до остановки
 -мезонов
с временем жизни
-мезонов
с временем жизни
 с,
так и на лету, когда они движутся со
скоростью, близкой к скорости света.
Времена жизни связаны соотношением
с,
так и на лету, когда они движутся со
скоростью, близкой к скорости света.
Времена жизни связаны соотношением
 ,
(10)
,
(10)
где
 - время жизни покоящихся
-мезонов,
а
- время жизни покоящихся
-мезонов,
а
 - - время жизни движущихся
-мезонов.
Если бы время жизни не зависело от
скорости они бы пролетали путь
- - время жизни движущихся
-мезонов.
Если бы время жизни не зависело от
скорости они бы пролетали путь
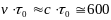 м.
м.
В действительности мюоны проходят путь около 20 км. Такому пробегу отвечает время жизни
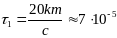 с
с .
.
Релятивистское изменение времени жизни здесь большой и, так сказать, вполне реальный эффект.
Парадокс близнецов
Пусть
мы наблюдаем из некоторой инерциальной
системы отсчета движущиеся произвольным
образом относительно нас часы. В каждый
момент времени можно ввести неподвижно
связанную с часами систему координат,
которая
будет
инерциальной. Тогда промежуток времени
 по
движущимся часам будет связан с
промежутком времени по неподвижным
часам
по
движущимся часам будет связан с
промежутком времени по неподвижным
часам
 формулой
формулой
 .
(1)
.
(1)
Интегрируя это соотношение, имеем
 .
(2)
.
(2)
Отсюда видно, что собственное время всегда меньше.
Преобразование скорости
Имеем
 ,
(1)
,
(1)
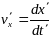 .
(2)
.
(2)
Запишем формулы обратного преобразования
 ,
(3)
,
(3)
 (4)
(4)
, (5)
(6)
Возьмем дифференциал от этих соотношений. Получим
 .
(7)
.
(7)
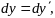 (8)
(8)
 ,
(9)
,
(9)
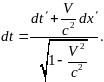 (10)
(10)
Отсюда получаем
 (11)
(11)
 ,
(12)
,
(12)
 .
(13)
.
(13)
В формулах, выражающих «штрихованные» скорости через «нештрихованнные» изменяются штрихи и знак у скорости.
Рассмотрим пример.
Пусть
в
частица движется со скоростью света
 .
Тогда в системе отсчета
ее скорость равна
.
Тогда в системе отсчета
ее скорость равна

как и должно быть!
Инварианты. Интервал между событиями.
В теории относительности много величин –инвариантов, которые не зависят от выбора системы отсчета. Одна из них – скорость распространения взаимодействия в вакууме. Важным инвариантом является интервал между событиями
 (1)
(1)
Прямым вычислением можно показать, что
 .
.
Поэтому
утверждение «два физических события
разделены интервалом
 »
справедливо во всех инерциальных
системах отсчета.
»
справедливо во всех инерциальных
системах отсчета.
Функция Лагранжа и принцип наименьшего действия
Основное требование СТО – релятивистская ковариантность уравнений механики. Т.е. запись их в такой форме, чтобы они были справедливы в любой инерциальной форме отсчета. Этому требованию легко удовлетворить, если использовать принцип наименьшего действия. Формула для действия
 .
(1)
.
(1)
Более подробно:
Каждая механическая система характеризуется определённой функцией
 .
.
В точках 1 и 2 задаются координаты частицы и соответствующие моменты времени. Тогда между этими положениями система движется так, чтобы интеграл
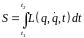 (1)
(1)
имел наименьшее возможное значение. Данный интеграл называется действием. Принцип наименьшего действия можно записать в виде
 (2)
(2)
Интеграл
должен быть равен нулю при произвольных
значениях
 . Это возможно только в том случае, когда
подынтегральное выражение тождественно
обращается в нуль. Получаем уравнение
. Это возможно только в том случае, когда
подынтегральное выражение тождественно
обращается в нуль. Получаем уравнение
 (3)
(3)
Это уравнение может быть записано в виде
 .
(4)
.
(4)
Величину
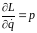 (5)
(5)
наз. обобщённым импульсом, а величину
 (6)
(6)
наз. обобщённой силой.
В частном случае свободной частицы в нерелятивистской механике
 .
(7)
.
(7)
Интеграл
(1) не должен зависеть от выбора той или
иной инерциальной системы отсчета.
Поэтому он должен быть взят от скаляра.
Единственный скаляр для свободной
частицы есть
 ,
где
,
где
 -постоянная
инвариантная величина. Рассмотрим
действие для релятивистской частицы
-постоянная
инвариантная величина. Рассмотрим
действие для релятивистской частицы
 .
(2)
.
(2)
Приведем (2) к виду (1). Имеем
 .
(3)
.
(3)
Поэтому
 .
(6)
.
(6)
Отсюда следует
 .
(7)
.
(7)
Значение
найдем из принципа соответствия. При
 имеем
имеем
 ,
(8)
,
(8)
 .
(9)
.
(9)
Так как в нерелятивистском случае
 ,
(10)
,
(10)
то следует положить
 .
(11)
.
(11)
При этом в нерелятивистском случае
 .
(12)
.
(12)
Отметим, что в нерелятивистском случае энергия и функция Лагранжа определяются с точностью до постоянного слагаемого.
Итак, в релятивистском случае
 .
(13)
.
(13)
Некоторые сведения из математики
Частная производная
 при
при

 ,
,

Поток
вектора
 через поверхность
через поверхность
Поверхность
разбивается на малые участки. Каждый
такой участок можно считать плоским.
К каждому участку проводится единичный
вектор нормали
 с направлением в соответствии с правилом
правого буравчика. Определяется проекция
вектора
на направление
с направлением в соответствии с правилом
правого буравчика. Определяется проекция
вектора
на направление
нормали. Далее эти проекции умножаются на соответствующие площади каждого малого участка и полученные результаты складываются. Получаем
 .
.
Если поверхность является замкнутой, то принято обозначение
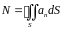 .
.
Определение дивергенции
 .
.
Определение ротора

Теорема Гаусса-Остроградского

Теорема Стокса




Энергия и импульс свободной частицы
Известно, что
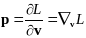 ,
(1)
,
(1)
и
 .
(2)
.
(2)
Поэтому
 .
(3)
.
(3)
Далее имеем
 .
.
В нерелятивистском случае
 .
(6).
.
(6).
В
процессах, в которых есть изменение
массы, величину
 необходимо
учитывать. Если масса изменяется, то
соответствующее изменение энергии
определяется по формуле
необходимо
учитывать. Если масса изменяется, то
соответствующее изменение энергии
определяется по формуле
 .
.
Были
проведены опыты по превращению покоящегося
электрона и позитрона в два
 -кванта.
Суммарная энергия
-квантов
в точности равна сумме энергий покоя
электрона и позитрона.
-кванта.
Суммарная энергия
-квантов
в точности равна сумме энергий покоя
электрона и позитрона.
